Python函数
函数
数学定义：y=f(x)，y是x的函数，x是自变量。
Python函数定义：由若干语句组成的语句块，函数名称，参数列表构成，它是组织代码的最小单元，完成一定功能。
函数的作用：结构化编程对代码最基本的封装，一般按照功能组织一段代码，封装后便于重复使用，使代码更加简洁美观。
函数的分类：内建函数，如：max()，库函数，如：random.randint()，自定义函数，使用def关键字定义。
1 # 名称为自定义标识符，括号里定义形参（形参可以用'='加入缺省值，一个'*'收集多个位置参数组织到元组中，两个'*'收集多个关键字参数组织到字典中，只能放最后） 2 def f(a, b=7, *args, c, d=8, **kwargs): # 一个'*'后只能使用关键字传参，Python3.8后增加符号为'/'，'/'前的参数必须用位置传参的方式，不能使用关键字传参 3 print(a, b, c, d) # 1 2 4 8 4 print(args) # (3,)，如果没接收到元素返回空元组 5 print(kwargs) # {'e': 5, 'f': 6}，如果没接收到元素返回空字典 6 return type(a), type(args), type(kwargs) # 返回一个元组，如果不写return返回None。在函数中执行到return后立刻跳出当前函数，返回 7 # 调用f函数，函数必须在调用前定义好，否则NameErrors，传入实参(分为位置传参与关键字传参，关键字传参必须在位置传参后面，不能重复传入参数) 8 y = f(*[1, 2], 3, **{'c': 4, 'e': 5}, f=6) # 一个'*'解构位置传参，如果结构的是集合注意无序，两个'*'解构关键字传参Python3.6版本后字典记录录入顺序 9 print(y) # (<class 'int'>, <class 'tuple'>, <class 'int'>, <class 'dict'>)，y接受f函数返回的元素
函数作用域
一个标识符的可见范围就是该标识符的作用域。作用域分为全局作用域和局部作用域，全局作用域在整个程序运行环境中可见，称为全局变量，局部作用域在函数，类等内部可见，称为本地变量。
嵌套函数
函数里面定义了另一个函数，外部的函数看不见里面的函数变量，里面的函数赋值右边需要用到的变量在里面没有被定义时，会在最近的外部范围找，赋值左边的标识符均定义为局部变量，只能在内部寻找。
global
在函数里使用该语句声明该变量为全局变量，尽量不要使用。
nonlocal
在函数里使用该语句声明该变量在最近的外部函数。
闭包
出现在嵌套函数中，内层函数用到了外层函数的变量，就形成了闭包。
匿名函数：lambda表达式
没有名字的函数是为匿名函数。
1 print((lambda x, y: x+y)(1, 2)) # 3，lambda后面跟参数，冒号后面是函数表达式，只能写一行，通常用于高阶函数，后面是传参内容，通常不用这种方式传参
递归函数
函数的执行流程跟栈有关，后入先出。递归函数是间接或直接调用函数自身，递归有深度限制，运行效率相对低，绝大多数递归都可用循环实现，能不用递归则不用。
1 def fib_(n, a=0, b=1): # 斐波那契数列递归 2 return b if n == 1 else fib_(n-1, b, a+b) 3 4 5 print(fib_(101)) # 573147844013817084101
生成器函数
生成器除了用生成器表达式外，还可以使用生成器函数，函数中存在yield语句的函数算是生成器函数，返回生成器对象。
1 def fib(a=0, b=1): # 斐波那契数列生成器函数 2 def inc(): 3 nonlocal a, b 4 a, b = b, a+b 5 yield a 6 return lambda: next(inc()) 7 8 9 f = fib() 10 for i in range(5): 11 print(f()) # 1 1 2 3 5
生成器交互
python提供了生成器交互的方法send，该方法可以与生成器沟通
def counter(): def inc(): a = 0 while True: a += 1 b = yield a if b is not None: a = 0 c = inc() return lambda d=False: c.send(0) if d else next(c) f = counter() print(f()) # 1 print(f()) # 2 print(f()) # 3 print(f(True)) # 1 print(f()) # 2
yield from
1 def counter(): # 一种简化语法的方法 2 def inc(): 3 yield from range(1000) 4 c = inc() 5 return lambda: next(c) 6 7 8 f = counter() 9 print(f()) # 0 10 print(f()) # 1 11 print(f()) # 2
高阶函数
数学概念：y = f(g(x))
接受一个或多个函数做参数，或输出一个函数的是为高阶函数。
内建高阶函数
1 print(sorted(['a', 'd', 1, 11, 22], key=lambda x: int(x, 16) if isinstance(x, str) else x)) # [1, 'a', 11, 'd', 22]，按十六进制排序 2 print(list(filter(lambda x: x % 3 == 0, range(10)))) # [0, 3, 6, 9]，过滤能被3整除的数 3 print(list(map(str, range(5)))) # ['0', '1', '2', '3', '4']，映射0-4为文本
插入排序
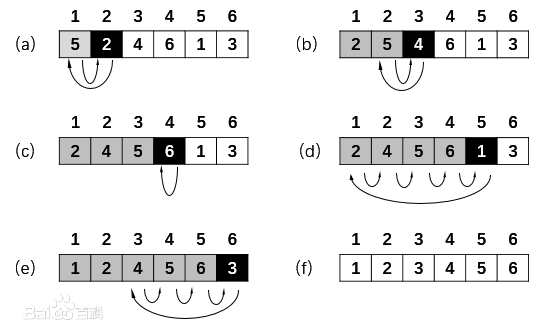
1 def sorted_1(ls): 2 for i in range(1, len(ls)): 3 a = ls[i] 4 for j in range(i-1, -1, -1): 5 if a < ls[j]: 6 ls[j+1] = ls[j] 7 else: 8 ls[j+1] = a 9 break 10 else: 11 ls[0] = a 12 return ls 13 14 15 arr = [5, 2, 4, 6, 1, 3] 16 print(sorted_1(arr)) # [1, 2, 3, 4, 5, 6]
1 def sorted_2(ls): 2 ls = [0] + ls 3 for i in range(1, len(ls)): 4 ls[0], j = ls[i], i-1 5 while ls[j] > ls[0]: 6 ls[j + 1], j = ls[j], j-1 7 else: 8 ls[j + 1] = ls[0] 9 return ls[1:] 10 11 12 arr = [5, 2, 4, 6, 1, 3] 13 print(sorted_2(arr)) # [1, 2, 3, 4, 5, 6]
树
定义
树（tree）是包含n（n>=0）个结点的有穷集，其中：
（1）每个元素称为结点（node）；
（2）有一个特定的结点被称为根结点或树根（root）。
（3）除根结点之外的其余数据元素被分为m（m≥0）个互不相交的集合T1，T2，……Tm-1，其中每一个集合Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）。
树也可以这样定义：树是由根结点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点，或称为树根。
我们可以形式地给出树的递归定义如下:
单个结点是一棵树，树根就是该结点本身。
设T1,T2,..,Tk是树，它们的根结点分别为n1,n2,..,nk。用一个新结点n作为n1,n2,..,nk的父亲，则得到一棵新树，结点n就是新树的根。我们称n1,n2,..,nk为一组兄弟结点，它们都是结点n的子结点。我们还称T1,T2,..,Tk为结点n的子树。
空集合也是树，称为空树。空树中没有结点。
名词解释
结点的度：一个结点含有的子结点的个数称为该结点的度；
叶结点或终端结点：度为0的结点称为叶结点；
非终端结点或分支结点：度不为0的结点；
双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；
孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；
兄弟结点：具有相同父结点的结点互称为兄弟结点；
树的度：一棵树中，最大的结点的度称为树的度；
结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推；
树的高度或深度：树中结点的最大层次；
堂兄弟结点：双亲在同一层的结点互为堂兄弟；
结点的祖先：从根到该结点所经分支上的所有结点；
子孙：以某结点为根的子树中任一结点都称为该结点的子孙。
森林：由m（m>=0）棵互不相交的树的集合称为森林。
特点
唯一的根
子树不相交
可以有0个或多个后继，除了根以外，只能有1个前驱
根没有前驱，叶子结点没有后继
双亲比孩子的层次小1
二叉树
在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。
满二叉树
一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。
完全二叉树
完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
性质：
如果一棵具有n个结点的深度为k的二叉树，它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应，这棵二叉树称为完全二叉树。
可以根据公式进行推导，假设n0是度为0的结点总数（即叶子结点数），n1是度为1的结点总数，n2是度为2的结点总数，则 ：
①n= n0+n1+n2 （其中n为完全二叉树的结点总数）；又因为一个度为2的结点会有2个子结点，一个度为1的结点会有1个子结点，除根结点外其他结点都有父结点，
②n= 1+n1+2*n2 ；由①、②两式把n2消去得：n= 2*n0+n1-1，由于完全二叉树中度为1的结点数只有两种可能0或1，由此得到n0=n/2 或 n0=(n+1)/2。
简便来算，就是 n0=n/2，其中n为奇数时（n1=0）向上取整；n为偶数时（n1=1）向下取整。可根据完全二叉树的结点总数计算出叶子结点数。
特点：
叶子结点只可能在最大的两层上出现,对任意结点，若其右分支下的子孙最大层次为L，则其左分支下的子孙的最大层次必为L 或 L+1；
出于简便起见,完全二叉树通常采用数组而不是链表存储,其存储结构如下:
var tree:array[1..n]of longint;{n:integer;n>=1}
对于tree[i]，有如下特点：
（1）若i为奇数且i>1，那么tree的左兄弟为tree[i-1]；
（2）若i为偶数且i<n，那么tree的右兄弟为tree[i+1]；
（3）若i>1，tree的父亲节点为tree[i div 2]；
（4）若2*i<=n，那么tree的左孩子为tree[2*i]；若2*i+1<=n，那么tree的右孩子为tree[2*i+1]；
（5）若i>n div 2,那么tree[i]为叶子结点（对应于（3））；
（6）若i<(n-1) div 2.那么tree[i]必有两个孩子（对应于（4））。
（7）满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。
完全二叉树第i层至多有2^（i-1）个节点，共i层的完全二叉树最多有2^i-1个节点。
完全二叉树的特点是：
1）只允许最后一层有空缺结点且空缺在右边，即叶子结点只能在层次最大的两层上出现；
2）对任一结点，如果其右子树的深度为j，则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个