You have a fraction 
. You need to find the first occurrence of digit c into decimal notation of the fraction after decimal point.
The first contains three single positive integers a, b, c (1 ≤ a < b ≤ 105, 0 ≤ c ≤ 9).
Print position of the first occurrence of digit c into the fraction. Positions are numbered from 1 after decimal point. It there is no such position, print -1.
1 2 0
2
2 3 7
-1
Hint
The fraction in the first example has the following decimal notation: 
. The first zero stands on second position.
The fraction in the second example has the following decimal notation: 
. There is no digit 7 in decimal notation of the fraction.
题意：a/b 看小数的第几位是c
#include <iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
int main()
{
int a,b,c,ge;
scanf("%d%d%d",&a,&b,&c);
ge=0;
for(int i=0;i<=999;i++)
{
ge++;
a*=10;
int d=a/b;
a%=b;
if(d==c)
{
printf("%d
",ge);
return 0;
}
}
printf("-1
");
return 0;
}
You have n distinct points on a plane, none of them lie on OY axis. Check that there is a point after removal of which the remaining points are located on one side of the OY axis.
The first line contains a single positive integer n (2 ≤ n ≤ 105).
The following n lines contain coordinates of the points. The i-th of these lines contains two single integers xi and yi (|xi|, |yi| ≤ 109, xi ≠ 0). No two points coincide.
Print "Yes" if there is such a point, "No" — otherwise.
You can print every letter in any case (upper or lower).
3
1 1
-1 -1
2 -1
Yes
4
1 1
2 2
-1 1
-2 2
No
3
1 2
2 1
4 60
Yes
In the first example the second point can be removed.
In the second example there is no suitable for the condition point.
In the third example any point can be removed.
题意：问能不能通过移动最多一个点使得全部点在y轴的一侧
#include <iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
struct p
{
int a;
int b;
}x[100000];
int main()
{
int n,ge1=0,ge2=0,i,j;
scanf("%d",&n);
for(i=0;i<=n-1;i++)
{
scanf("%d%d",&x[i].a,&x[i].b);
if(x[i].a>0)
ge1++;
if(x[i].a<0)
ge2++;
}
if(ge2==n||ge1==n)
printf("Yes
");
else
{
if(ge1==n-1||ge2==n-1)
printf("Yes
");
else
printf("No
");
}
}
Pig is visiting a friend.
Pig's house is located at point 0, and his friend's house is located at point m on an axis.
Pig can use teleports to move along the axis.
To use a teleport, Pig should come to a certain point (where the teleport is located) and choose where to move: for each teleport there is the rightmost point it can move Pig to, this point is known as the limit of the teleport.
Formally, a teleport located at point x with limit y can move Pig from point x to any point within the segment [x; y], including the bounds.
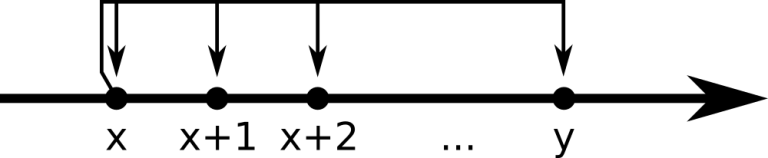
Determine if Pig can visit the friend using teleports only, or he should use his car.
The first line contains two integers n and m (1 ≤ n ≤ 100, 1 ≤ m ≤ 100) — the number of teleports and the location of the friend's house.
The next n lines contain information about teleports.
The i-th of these lines contains two integers ai and bi (0 ≤ ai ≤ bi ≤ m), where ai is the location of the i-th teleport, and bi is its limit.
It is guaranteed that ai ≥ ai - 1 for every i (2 ≤ i ≤ n).
Print "YES" if there is a path from Pig's house to his friend's house that uses only teleports, and "NO" otherwise.
You can print each letter in arbitrary case (upper or lower).
3 5
0 2
2 4
3 5
YES
3 7
0 4
2 5
6 7
NO
The first example is shown on the picture below:
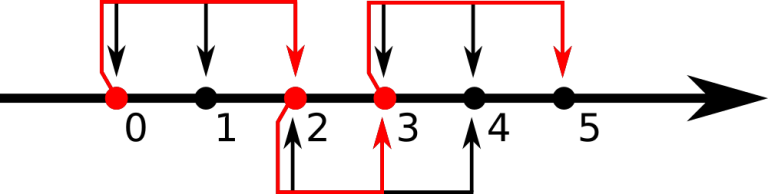
Pig can use the first teleport from his house (point 0) to reach point 2, then using the second teleport go from point 2 to point 3, then using the third teleport go from point 3 to point 5, where his friend lives.
The second example is shown on the picture below:
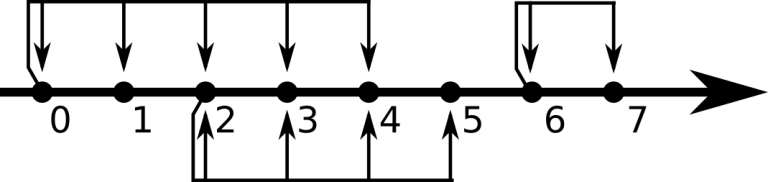
You can see that there is no path from Pig's house to his friend's house that uses only teleports.
#include <iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
struct p
{
int a;
int b;
} x[1010];
int main()
{
int m,n,l,r,i;
l=r=0;
scanf("%d%d",&m,&n);
for(i=0; i<=m-1; i++)
{
scanf("%d%d",&x[i].a,&x[i].b);
}
for(i=0; i<=m-1; i++)
{
if(x[i].a<=r)
{
if(x[i].b>r)
r=x[i].b;
}
else
break;
}
if(r>=n)
printf("YES
");
else
printf("NO
");
}
You are given an integer N. Consider all possible segments on the coordinate axis with endpoints at integer points with coordinates between 0 and N, inclusive; there will be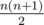 
of them.
You want to draw these segments in several layers so that in each layer the segments don't overlap (they might touch at the endpoints though). You can not move the segments to a different location on the coordinate axis.
Find the minimal number of layers you have to use for the given N.
The only input line contains a single integer N (1 ≤ N ≤ 100).
Output a single integer - the minimal number of layers required to draw the segments for the given N.
2
2
3
4
4
6
As an example, here are the segments and their optimal arrangement into layers for N = 4.
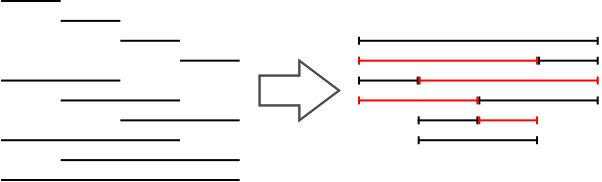
#include <iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
struct p
{
int l,r;
int flag;
int ge;
} x[10100];
int cmp(struct p a,struct p b)
{
if(a.l!=b.l)
return a.l<b.l;
else
return a.r<b.r;
}
int main()
{
int n,i,j;
scanf("%d",&n);
memset(x,0,sizeof(x));
int t=n*(n+1)/2;
int z=0;
for(i=0; i<=n-1; i++)
for(j=i+1; j<=n; j++)
{
x[z].l=i;
x[z++].r=j;
}
sort(x,x+z,cmp);
for(i=t-1; i>=0; i--)
{
if(x[i].flag==0)
{
int l=x[i].l;
for(j=i-1; j>=0; j--)
if(x[j].flag==0&&x[j].r==l)
{
l=x[j].l;
x[j].flag=1;
}
}
}
int ge=0;
for(i=0; i<=t-1; i++)
{
if(x[i].flag==0)
ge++;
}
printf("%d
",ge);
}