[hihocoder 1033]交错和 数位dp/记忆化搜索

#1033 : 交错和

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描写叙述

给定一个数 x，设它十进制展从高位到低位上的数位依次是 a0, a1, ..., an - 1，定义交错和函数：

f(x) = a0 - a1 + a2 - ... + ( - 1)n - 1an - 1

比如：

f(3214567) = 3 - 2 + 1 - 4 + 5 - 6 + 7 = 4

给定 

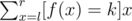
输入

输入数据仅一行包括三个整数。l, r, k(0 ≤ l ≤ r ≤ 1018, |k| ≤ 100)。

输出

输出一行一个整数表示结果，考虑到答案可能非常大，输出结果模 109 + 7。

提示

对于例子 ，满足条件的数有 110 和 121，所以结果是 231 = 110 + 121。

很多其它例子：

Input

4344 3214567 3

Output

611668829

Input

404491953 1587197241 1

Output

323937411

Input

60296763086567224 193422344885593844 10

Output

608746132

Input

100 121 -1

Output

120

例子输入

100 121 0

例子输出

231

中文题=_=题目出处来自hihocoder第一次挑战赛，xiaodao出题。

刚開始做的时候脑洞开大了以为是数论专题，后来才发现是数位dp，几个easy易卡住的点：

1.记忆化搜索写的时候要将同样交错和的个数。同样交错和的数字的和分别进行dp

2.对于一位数字和两位数字的计算方式并不同样，要分数字的位数进行讨论。

3.因为结果可能比較大，每一步都须要使用同余定理，以防运算过程中爆long long的情况。

记忆化搜索的思路。

当前的交错和同样的数字的和=sum（待搜索的状态的数字和+当前搜索的数字的大小*当前搜索到的符合条件的数字个数）。

#include <cstdio>
#include <cstring>
long long mod=1000000007;
long long base[20];
long long l,r,k,bit[20],bt,yy;
struct node {
    long long s,n;//s代表数字和，n代表数字个数
};
node dp[20][400];//状态转移
node dfs(long long pos,long long target,long long limit)//数位dp，基本能够算是模板啦
{
    node t;
    t.s=t.n=0;
    if (pos==0) {               //处理到最后一位。直接推断返回
        if (target==100)
        t.n=1;
        return t;
    }
    if ((limit==0)&&(dp[pos][target].n!=-1)) return dp[pos][target];
    long long tail=limit?
bit[pos]:9;
    long long sgn=((yy-pos)%2)?
(-1):(1);//确定符号
    long long head;
    if (pos==yy)head =1;
    else head=0;//确定搜索的起点和终点
    for (int i=head;i<=tail;i++)
    {
        node tmp=dfs(pos-1,target-i*sgn,(limit==1)&&(i==bit[pos]));
        if ((tmp.n)>0){
            t.n+=tmp.n;
            long long q;
            q=((((tmp.n%mod)*base[pos])%mod)*i)%mod;//结果的同余处理
            t.s+=(tmp.s)%mod;
            t.s%=mod;
            t.s+=q;
            t.s%=mod;//每一步都要同余
        }
    }
    if (limit==0) dp[pos][target]=t;
    return t;
}
long long cal(long long x,long long y)
{
    long long ans=0;
    if (x==-1) return 0;
    if (x==0) return 0;
    bt = 0;
    while (x)
    {
        bt++;
        bit[bt]=x%10;
        x/=10;
    }
    for (yy=1;yy<=bt;yy++){
        memset(dp,-1,sizeof dp);
        ans+=dfs(yy,y+100,yy==bt).s;//对于每一个长度为yy的数字进行处理
        ans=(ans+mod)%mod;
    }
    return ans;
}
int main()
{
    base[1]=1;
    for (int i=2;i<=19;i++)
        base[i]=(base[i-1]*10)%mod;
    scanf("%lld%lld%lld",&l,&r,&k);
    {
        printf("%lld",(cal(r,k)-cal(l-1,k)+mod)%mod);
    }
    return 0;
}