麻麻,我们班的孩子都分为好几个帮派,我要怎么做才能知道他们总共分了有几个帮派呀,我要怎么才能知道他们有没有人同时在两个帮派呀;
接下来就进入我们的并查集专题,英文名称Union-Find。
并查集是一种用于不相交集合的数据结构,并查集通过几个操作来建立,修改,查找和维护一些不相交的集合,一般用于不相交集合的合并问题,他也衍生出许多其他的应用,图论中就会用并查集判环的操作,并查集还有着其他更为广泛
的应用。
由于计算机经常会遇到数据量很大的情况,或者要反复查询某个元素所属的集合,这类问题并查集统统搞定。
首先我们介绍一下他的基本操作:
Init_set(v):建立集合操作,初始化每个元素单独成为一个集合。
find(v):查找操作,我们用一个集合中其中一个元素的下标来表示这个集合,用二叉树表示的话就是二叉树的根,这个函数会返回v的最上层节点,即这个二叉集合数的根。
Join(x, y):合并操作,将包含x集合和y集合的两个集合合并为一个新的集合。
is_same(u, v):查重操作,如果元素u和v在同一个集合中则返回true;否则返回false。
下面我们给出这些操作的基本代码:
1 #include <cstdio> 2 using namespace std; 3 4 const int maxn = 1e6 + 5; 5 int n, head[maxn]; 6 7 void Init_set() { 8 for(int i = 1; i <= n; i ++) head[i] = i; 9 } 10 11 int find(int u) { 12 if(head[u] == u) return u; 13 return find(head[u]); 14 } 15 16 void Join(int x, int y) { 17 int fx = find(x), fy = find(y); 18 if(fx != fy) head[fx] = fy;//我们把y的根节点的父亲点设为x的最上层结点就行了 19 } 20 21 int is_same(int u, int v) { 22 return (find(u) == find(v)); 23 }
下面给出一个并查集的样例:
以5个结点为例,圆圈内为结点的标号,我们用head数组记录每个结点的父亲结点,head[i]表示i结点的父亲节点的标号,当head[i] = i时,结点i的父节点是它本身,那么i的所在的树的根就是i。
初始化,head[i] = i,他们分别独立成为一个集合,分别作为自己的父节点。
Init:
head[ i ] = i;
![]()
合并1和2时,2的父节点变为1,head[2] = 1, 此时有
head[1] = 1; head[2] = 1, head[3] = 3, head[4] = 4, head[5] = 5;

如果我们现在分别查找1和2结点所在树的根节点,1结点所在的树的根节点为1,2结点所在树的根节点也是1,也就是说1和2此时位于根结点为1
的同一颗树内。
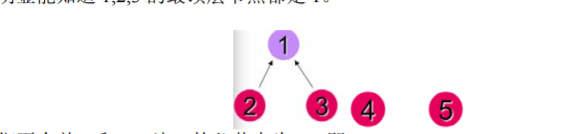
接下来我们合并1和3,让head[3] = 1,即使得3的父节点为1,有
head[1] = 1; head[2] = 1, head[3] = 1, head[4] = 4, head[5] = 5;
很明显能知道1,2,3的最顶层节点都是1。
我们在合并4和5,让4的父节点变为5,即head[4] = 5;

最后我们合并5和3,让5的父节点为3,即head[5] = 3。可以得出如下的图。
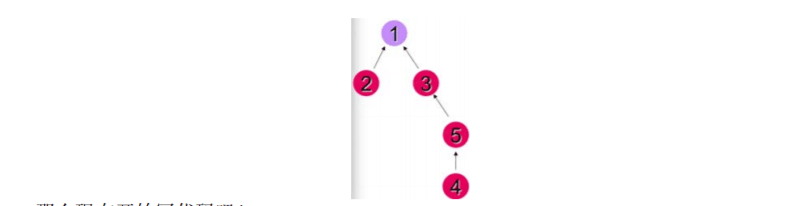
在上述算法中很容易可以看出,每个结点都有一个根结点,而两个集合合并时会以其中一个集合的根节点为新集合的根节点将另一个集合插入,即形成了一颗二叉树。
观察上述算法,可以发现基本所有操作都是基于find函数的,所以我们可以想可不可以有优化呢?我们发现初始化每个结点只进行一次,但是find和join都会进行多次,所以如果程序很大的话跑起来非常吃力。
下面我们就介绍两种对该算法的优化:
路径压缩:这种策略非常的简单高效。正如下面的代码中,在find操作之后,使用这种策略会使得查找路径中的每个结点直接指向根结点,路径压缩并不需要改变其余的任何东西。
1 int find(int u) {
2 if(head[u] == u) return u;
3 return head[u] = find(head[u]);
4 }
按秩合并:这种做法就是使具有较少结点的树的根指向具有较多结点的树的根。对于每个结点,我们维护一个rank值,通过比较rank值我们进行相应的操作。
1 #include <cstdio> 2 using namespace std; 3 4 const int maxn = 1e6 + 5; 5 int n, head[maxn], rank[maxn]; 6 7 void Init_set() { 8 for(int i = 1; i <= n; i ++) { 9 head[i] = i; 10 rank[i] = 0; 11 } 12 } 13 14 int find(int u) { 15 if(head[u] == u) return u; 16 return head[u] = find(head[u]); 17 } 18 19 void join(int x, int y) { 20 int fx = find(x), fy = find(y); 21 if(fx == fy) return; 22 if(rank[fx] > rank[fy]) 23 head[fy] = fx; 24 else { 25 head[fx] = fy; 26 if(rank[fx] == rank[fy]) rank[fy] += 1;//最重要的是修改祖先的rank,所以只需要修改祖先的rank,子孙的rank不用管 27 } 28 } 29 30 int is_same(int u, int v) { 31 return (find(u) == find(v)); 32 }
后续跟进并查集的相关题目......