带权并查集

　　学习带权并查集之前我们需要先对并查集和路径压缩压缩了解，有需求的可以参考这篇博客。

刚昨天总结了并查集的相关操作，今天做题的时候居然发现自己一直都是存在一些想不到的地方，总是会存在一些漏洞，最骚的是今天做到了食物链这道题......才知道了带权并查集和种类并查集......好了接下

来就要进入带权并查集了。

　　上面的博客中有写到路径压缩的相关操作，我们知道路径压缩的结果就是同一集合中的所有元素统一指向树根，这样可以加快访问速度。和路径压缩一样，带权并查集仅仅是在每个集合元素都指向树根

的前提下赋予这些结点相对于树根的权值。

　　那么我们就需要用一个数组一个元素相对于他所属集合树根的权值，我们用value存储。

　　我们已经知道了基本并查集的一般实现，但是如果加入了value要如何实现呢。

　　

　　我们思考：

　　　　在find函数中，我们对于每个元素进行一次赋值，使得最终所有元素的父亲结点都指向树根结点，那么如果带有权值的话，我们知道每次都会改变一个结点的父亲，知道找到他所属集合的树根，所以

　　我们每次也需要更新对应的value值。

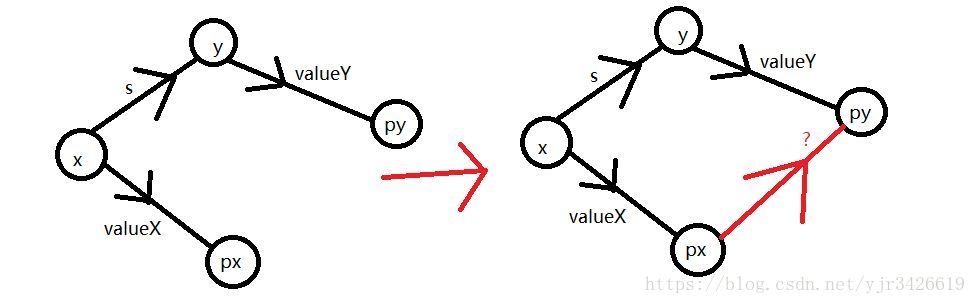
　　　　那么合并函数呢，我们知道每次合并我们会将x所属集合的树根px的父亲设置为y所属集合的树根py，这样就可以将两个集合合并，那么我们知道在这过程中我们改变了px的父亲，也就需要改变px对

应他父亲的权值，我们根据下图就可以知道，对于value[px]，因为x最终父亲为py，所以显然两条路的权值应该相等，我们就可以得出如下代码。

　　　　并不是所有类型的更新都是下面这种情况，具体情况具体分析，但是思路宝贵。

#include <cstdio>
#include <cstring>
using namespace std;

const int maxn = 10000 + 5;
int head[maxn], value[maxn], rank[maxn];

int find(int u) {
    if(u != head[u]) {
        int t = head[u];
        head[u] = find(head[u]);
        value[u] += value[t];
    }
    return head[u];
}

void Union_Set(int x, int y, int s) {
    int fx = find(x), fy = find(y);
    if(fx == fy) return;
    if(rank[fx] > rank[fy]) {
        head[fy] = fx;
        value[fy] = -value[y] + value[x] + s;
    } else {
        head[fx] = fy;
        value[fx] = -value[x] + value[y] + s;
        if(rank[fx] == rank[fy]) rank[fy] ++;
    }
}

int is_same(int x, int y) {
    return find(x) == find(y);
}

int main () {

    return 0;
}　　

　　后续会更新相关题目：针对题目再做详细描述。