前言
在实际应用场景中,很多时候我们会用到字典集的查找。通过一个键值key,去拿到它对应的值对象。这种方法确实很高效,很快,但是这里有个问题,当字典集储存的键值很多的情况时,毫无疑问,这里会消耗掉大量的内存空间。这个在我们做基数计数的统计应用时,这个空间会膨胀地特别厉害。本节笔者将要谈论的是对于基数统计来说,使用上更为适用的1种数据结构Trie Tree以及它的衍生优化版Radix Tree。
Trie Tree
我们先来看第一种树结构Trie Tree,名叫字典树。Trie Tree的原理是将每个key拆分成每个单位长度字符,然后对应到每个分支上,分支所在的节点对应为从根节点到当前节点的拼接出的key的值。它的结构图如下所示。
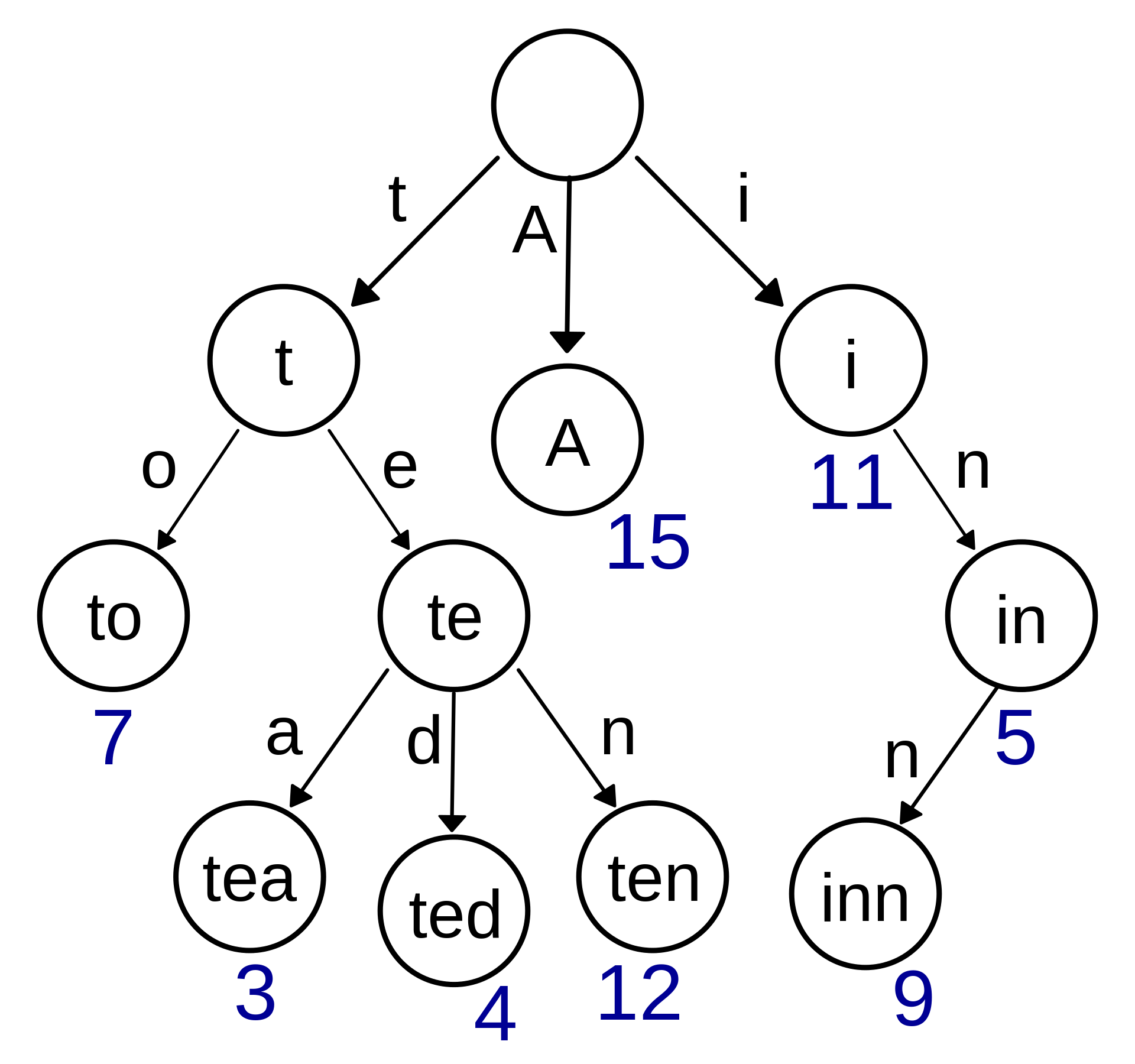
上图中每个节点存储的值为一个数值,当然这不是绝对的,我们可以假想这可以是key值所对应的任何值对象。只是计数统计在平时使用中更为常见一些。那么问题来了,相比较于字典集的存储方式,Trie Tree将key以树型结构构造,有什么用意呢?一个最大的帮助是公共的前缀被共享了,这样可以避免被重复地存储了。而在普通的字典集结构中,这种重复key前缀都是独立被包含在每个key内的。假设当字典集中所存储的key都带有大量重复的前缀时,Trie Tree将会消耗比普通字典结构更少的空间。
如上述所描述的,通过共享公共前缀的方式空间省了不少,但是它的查询效率如何呢?按照树的查询方式,一个查询key长度m,首先我们会将key拆分成m个字符,然后对应每个长度,从根节点依次向下,总共会进行到m次查找。因此我们可以得出,它的查询时间复杂度为O(m),随着查询key长度的增加,它所消耗的时间将会线性增长。
往深层面来看查询时间的问题,其实本质上这是树的深度引起的问题,对于长key而言,它的key对应的节点构造的深度过深。那么如果说我们将这“棵”树构造得更紧凑一些,会如何呢?于是我们有了另外一个衍生版本树:Radix Tree(基数树)。
Radix Tree
Radix Tree名为基数树,它的计数统计原理和Trie Tree极为相似,一个最大的区别点在于它不是按照每个字符长度做节点拆分,而是可以以1个或多个字符叠加作为一个分支。这就避免了长字符key会分出深度很深的节点。Radix Tree的结构构造如下图所示:
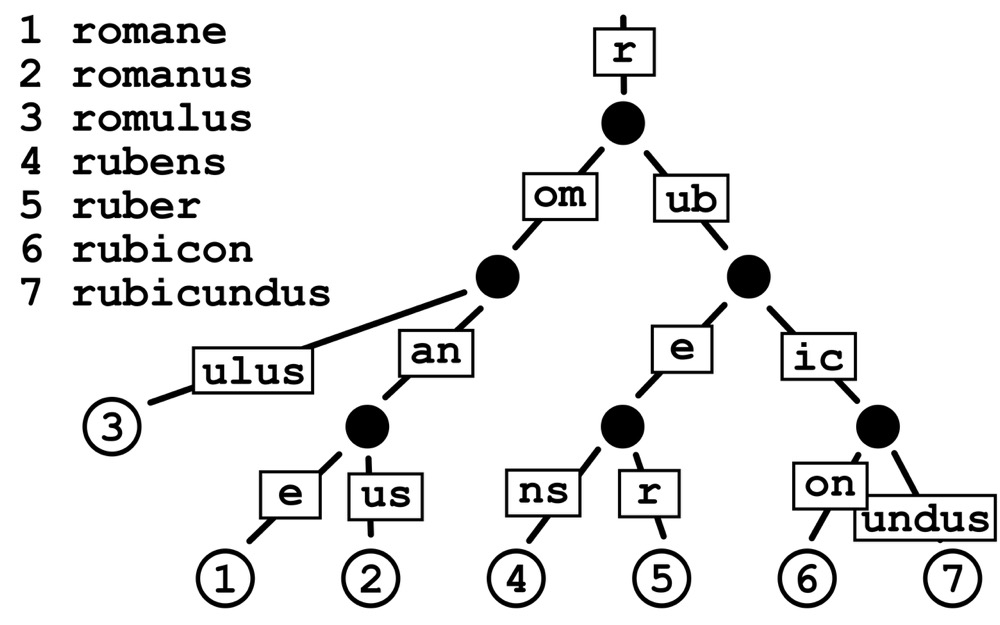
从上图我们可以看到,上面每个分支可以是局部部分字符串。以简单的字符查找为例,Radix Tree的搜索查找过程如下:
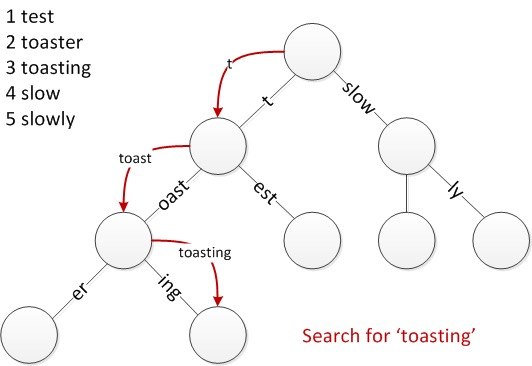
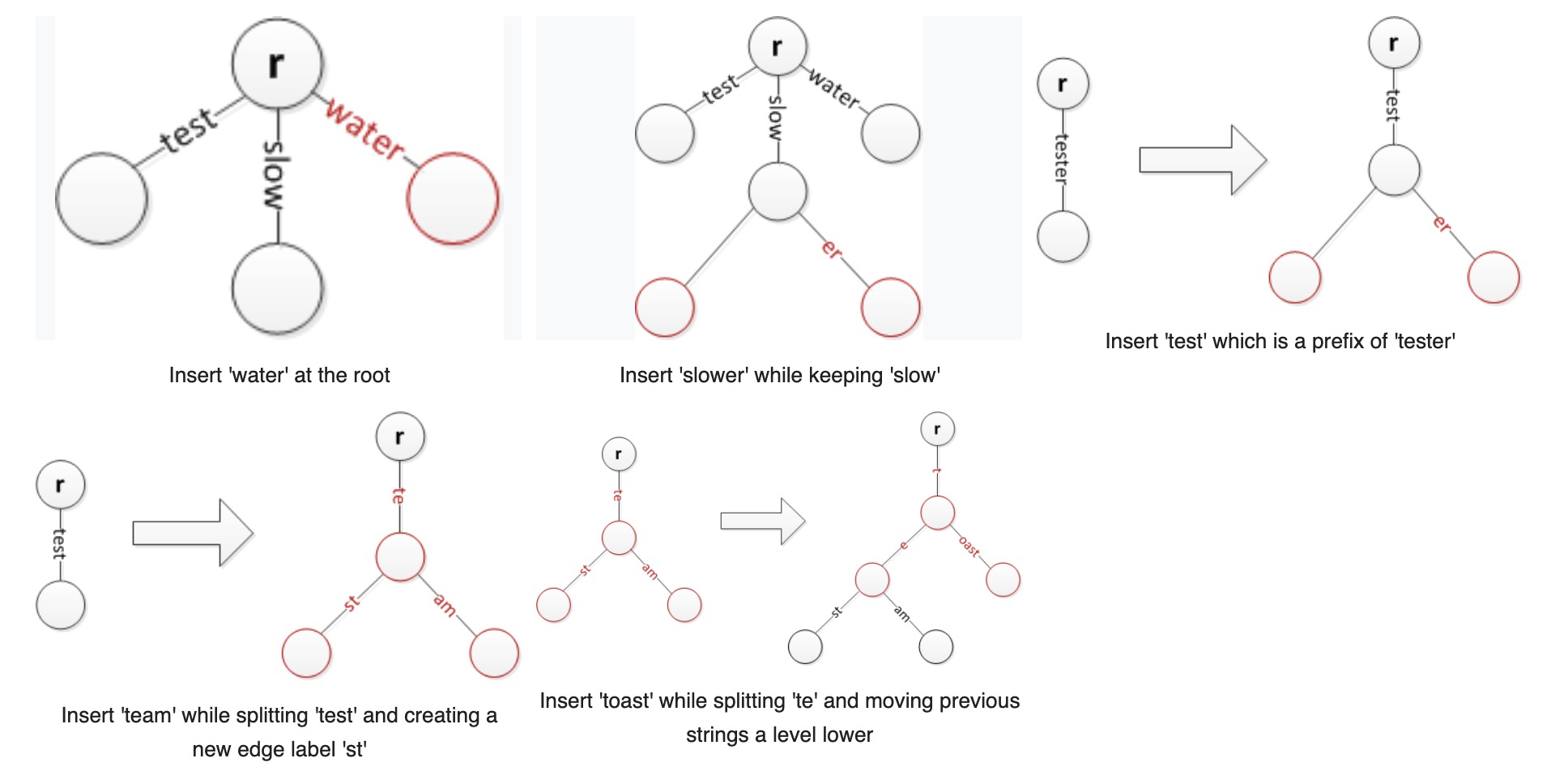
针对Radix Tree的构造规则,它的节点插入和删除行为相比较于Trie Tree来说,略有不同。
- 对于节点插入而言,当有新的key进来,需要拆分原有公共前缀分支。
- 对于节点删除而言,当删除一个现有key后,发现其父节点只有另外一个子节点key,则此子节点可以和父节点合并为一个新的节点,以此减少树的比较深度。
Radix Tree的insert过程如下图所示:
Trie Tree、Radix Tree的局限性
的确Trie Tree、Radix Tree在某些应用场景可以帮助我们节省内存使用空间,但是它们也有其使用的局限性。比如这类树结构无法适用于所有的数据类型,目前来看主要适用于能够用string字符等可作为表达式查询key的场景。
引用
[1].https://en.wikipedia.org/wiki/Radix_tree
[2].https://en.wikipedia.org/wiki/Trie