部分转载了洛谷上的题解:https://www.luogu.org/problemnew/solution/P1111
以及其他网站的图片及文字:https://www.cnblogs.com/MrSaver/p/9607552.html
- 并查集
作用:可以查询两个节点是否是在同一个集合内
存储结构:树形结构,但一般用一位数组就能够存下来。每一个数组的值a[i] = b 指的是结点i的父节点是结点b。存储就是这样简单。
- 查
目的:查找结点x的祖先结点是谁
示意图:其实就是数组的元素转移,有点类似于链表的遍历
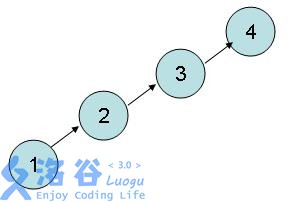
递归形式
int findfather(int x){ return x == a[x]?x:find(a[x]); }
循环形式
int findfather(int x){ while(x!=a[x]) x = a[x]; return x; }
- 集合的并
并就是讲两个节点合并到一个集合里面(这个集合必须是树),每个节点对应一个祖先,最老公共祖先的祖先就是自己,而每个节点在合并前的初始值也是自己,也就是:若有一个节点aa,设它的祖先为s[a]s[a],那么它的初始值就是s[a]=as[a]=a。这个合并操作并不难,只要判断一下这两个节点是否有祖先,没有就很好办,直接随便连,比如:aa和bb,他们都没有祖先(也就是祖先是自己),那么就可以s[a]=bs[a]=b了,如果s[a] \neq as[a]≠a,那么就让bb的最老祖先(可能是自己)再往上多一个祖先s[a]s[a],此时bb的最老祖先也就是aa的最老祖先了(不一定是aa)
将结点x所在的集合与y所在的集合合并起来
void join(int x,int y){ int fx = find(x),fy = find(y); //去找公共祖先 if(fx!=fy){ a[fx] = fy; } }
- 压缩路径
对于查操作,每次寻找祖先都需要遍历一遍路径,类似与像链表一样遍历数组,而我们的目的仅仅想只要它的祖先是谁,仅仅是查祖先,就和路径没多大关系。我们知道,一条路径上的结点的祖先都是同一个,只需要让这些点都指向祖先就行了。
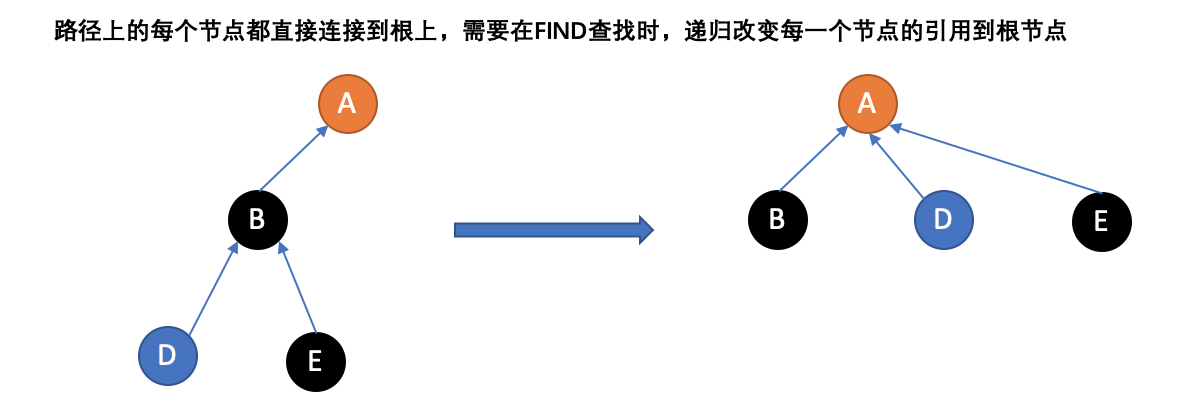
- 具体代码
递归形式
int findfather(int x){ if(x!=a[x]) a[x] = findfather(a[x]); return a[x]; }
循环形式
int findfather(int x){ int r = x; while(a[r] != r){ //找祖先 r = a[r]; } int rr = x; while(a[rr] != rr){ //把路径的节点都指向祖先 rr = a[rr]; a[rr] = r; } return r; }