机器学习-线性回归算法

三张手写推导过程

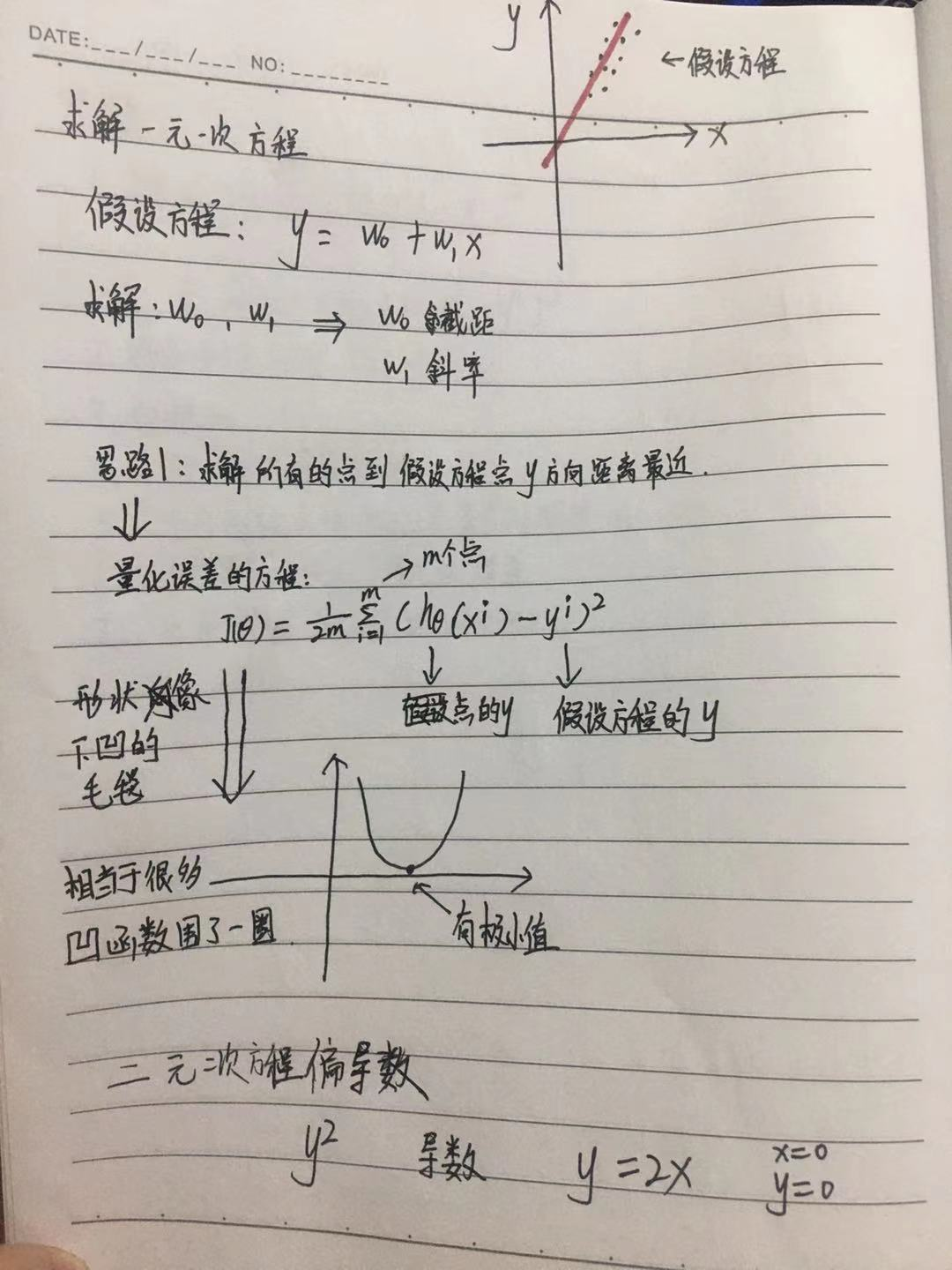
问：为什么不是求点到直线的垂直举例？

• 垂直距离会缩小误差，取y轴上的距离会放大误差，提高精度
• 不好计算

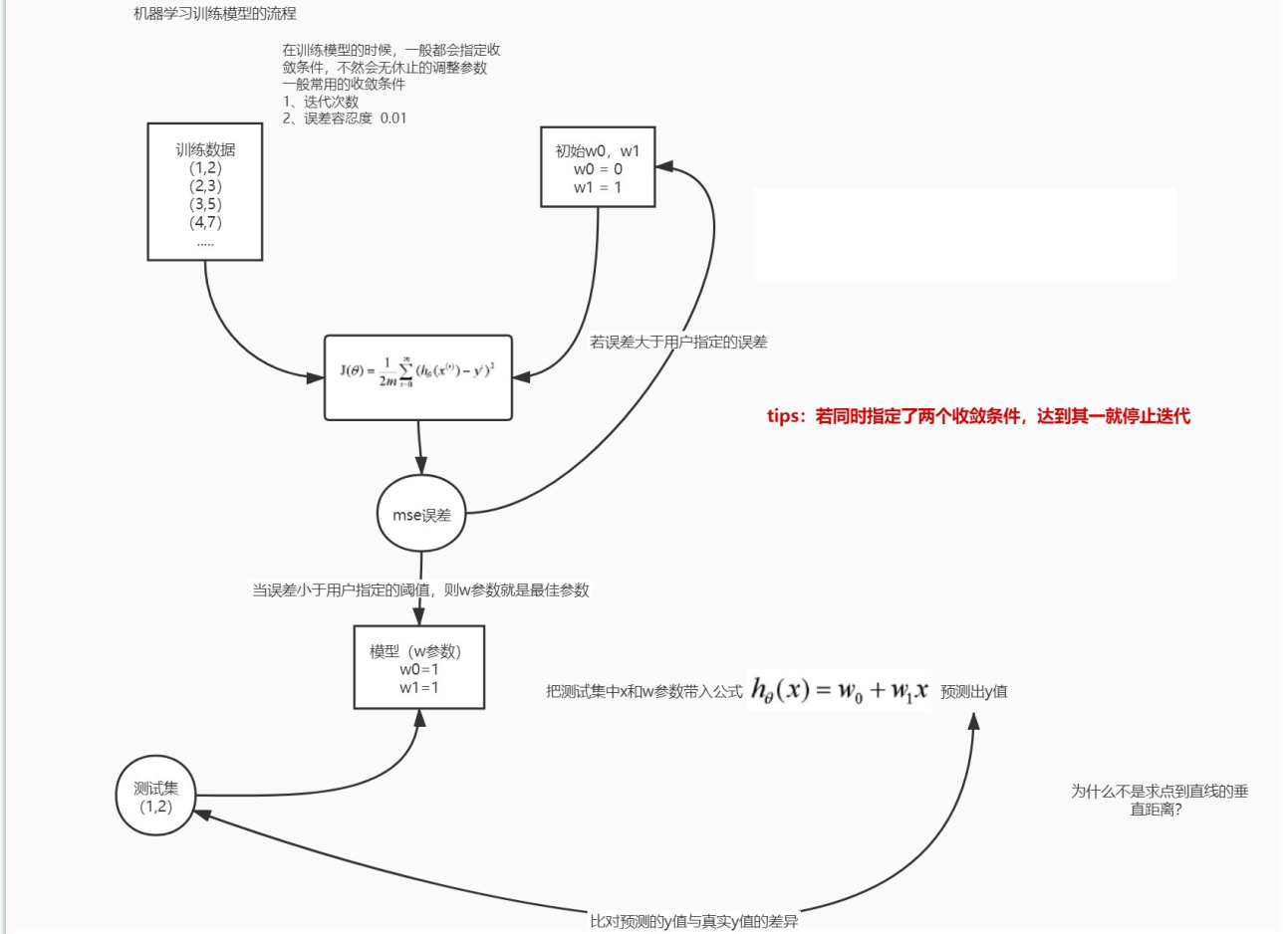
线性回归学习套路

1. 随机产生w参数
2. 把w参数与样本数据代入到误差函数中，求解误差值
3. 误差值与用户指定的误差阙值比较
4. 如果大于用户指定的误差阙值，继续调整w参数(2/3/4步骤)
5. 如果误差小于用户指定的误差阙值，那么此时的w参数就是最佳的w参数

 

梯度下降法：：

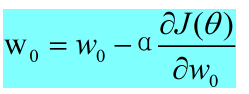
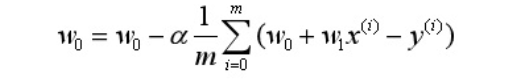
• 导数正负 决定了w参数调整方向 α决定了每次w调整的步长
• 导数小于0  w往大调整
• 导数大于0  w往小调整
• 注意： a不能太大，否则会梯度上升
• 注意:  也不可以 w0 = w0 - α   会成为永动机
  

 

代码实现

import numpy as np

def h(x):
    return w0 + w1 * x

if __name__ == '__main__':
    # α步长
    rate = 0.03
    # 准备的样本数据
    x_train = np.array([1,2,3,4,5,6,7,8,9])
    y_train = np.array([2, 3, 4, 5, 6, 7, 8, 9, 10])
    # 随机产生w0 w1
    w0 = np.random.normal()
    w1 = np.random.normal()

    err = 1


# 依据用户指定的误差阈值来收敛
while err > 0.001:
    for x, y in zip(x_train, y_train):
        # 使用梯度下降法， 每次训练处一个w0 w1 去下面计算
        w0 = w0 - rate * (h(x) - y)
        w1 = w1 - rate * (h(x) - y) * x


    value = 0.0
    for x,y in zip(x_train, y_train):
        # 损失函数、目标函数、误差函数
        value += (y - h(x)) ** 2  #将 h(x) = w0 + w1 * x 代入
        m = len(x_train)
        err = float(value / (2 * m))
        print("err: %f" % err)
print(w0, w1)