1.房价案例：
房价预测：我们有两个特征，临街宽度(frontage)和纵深(depth)，我们可以建立这样的线性回归模型，临街宽度是第一个特征x1,纵深是第二个特征x2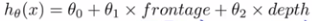
。这里我们可以自己选择特征值，将frontage 乘以 depth得到我们拥有土地的面积，于是我们就用这一个特征来计算
，有时通过定义新的特征，可以得到一个更好的模型。
与特征选择密切相关的一个概念是多项式回归。比如有下面这个住房价格的数据集，可能会有不同的模型用于拟合数据
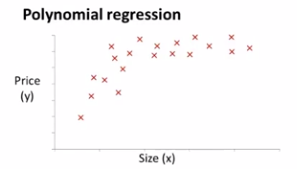
选择之一就是这样的一个二次模型，直线并不能很好的拟合这些数据，但是用下面这样的二次模型来拟合数据，价格可能是一个二次函数，可以得到下面这样的拟合结果：
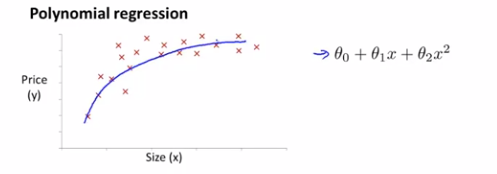
但是可能二次函数模型不合理，因为一个二次函数最终会降下来，我们不觉得随着土地面积的增加，房子价格会降下来，所以我们会选择一个不同的多项式模型，并转而选用一个三次函数，三次函数拟合的更好，因为它不会在最后下降，拟合的情况如下图
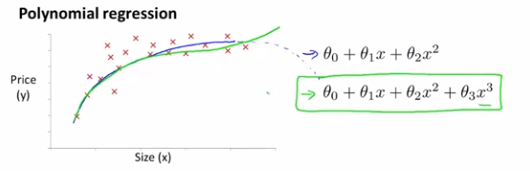
那么我们怎样将模型与数据进行拟合呢？使用多元线性回归的方法，
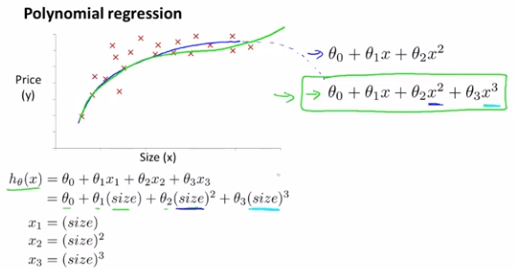
如果选择这样的模型来拟合，特征选择就显得更重要了，