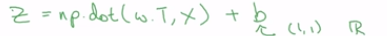1.不使用任何for循环用梯度下降实现整个训练集的一步迭代。
(0)我们已经讨论过向量化如何显著加速代码,在这次视频中我们会设计向量化是如何实现logistic回归,这样酒桶同时处理m个训练集,来实现梯度下降算法的一步迭代,不需要使用任何显式的for循环
(1)logistic回归正向传播的步骤:如果有m个训练样本,对一个样本进行预测,需要通过下面的方式计算出z值和激活函数a值,然后用同样的方法计算第二个和第三个样本...........以此类推,如果有m个样本的话,这样可能需要做上m次。
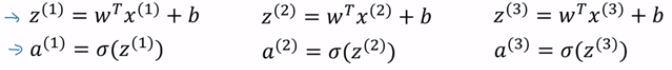
可以看出,为了执行正向传播的步骤,针对m各样本都需要计算出预测的结果,但是有一个办法不需要任何一个显示的for循环,
(2)定义矩阵X来作为训练的输入,像下面这个由m列堆叠在一起形成了nx x m的矩阵。首先要做的是计算z(1)、z(2)、z(3)等等,全部都在一个步骤中,我们先构建一个1xm的矩阵,实际上就是一个行向量,我们先计算z(1),z(2)等等一直到z(m),都是在同一时间内完成的,结果发现可以写成w的转置乘以大写的矩阵X再加上向量b,如下所示: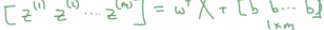 ,最后计算的结果如下:
,最后计算的结果如下:
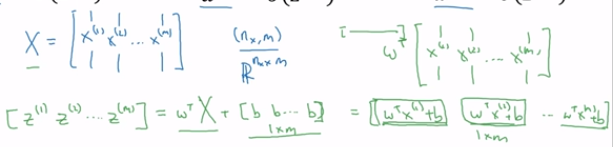
在numpy中的计算形式是: