在全局版的标准粒子群算法中,每个粒子的速度的更新是根据两个因素来变化的,这两个因素是:1. 粒子自己历史最优值pi。2. 粒子群体的全局最优值pg。如果改变粒子速度更新公式,让每个粒子的速度的更新根据以下两个因素更新,A. 粒子自己历史最优值pi。B. 粒子邻域内粒子的最优值pnk。其余保持跟全局版的标准粒子群算法一样,这个算法就变为局部版的粒子群算法。
一般一个粒子i 的邻域随着迭代次数的增加而逐渐增加,开始第一次迭代,它的邻域为0,随着迭代次数邻域线性变大,最后邻域扩展到整个粒子群,这时就变成全局版本的粒子群算法了。经过实践证明:全局版本的粒子群算法收敛速度快,但是容易陷入局部最优。局部版本的粒子群算法收敛速度慢,但是很难陷入局部最优。现在的粒子群算法大都在收敛速度与摆脱局部最优这两个方面下功夫。其实这两个方面是矛盾的。看如何更好的折中了。
根据取邻域的方式的不同,局部版本的粒子群算法有很多不同的实现方法。
第一种方法:按照粒子的编号取粒子的邻域,取法有四种:1,环形取法 2,随机环形取法 3,轮形取法 4,随机轮形取法。

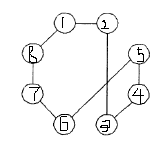
1 环形 2 随机环形


3 轮形 4随机轮形
环形取法为例:以粒子1为例,当邻域是0的时候,邻域是它本身,当邻域是1时,邻域为2,8;当邻域是2时,邻域是2,3,7,8;......,以此类推,一直到邻域为4,这个时候,邻域扩展到整个例子群体。据文献介绍(国外的文献),采用轮形拓扑结构,PSO的效果很好。
第二种方法:按照粒子的欧式距离取粒子的邻域
在第一种方法中,按照粒子的编号来得到粒子的邻域,但是这些粒子其实可能在实际位置上并不相邻,于是Suganthan提出基于空间距离的划分方案,在迭代中计算每一个粒子与群中其他粒子的距离。记录任何2个粒子间的的最大距离为dm。对每一粒子按照||xa-xb||/dm计算一个比值。其中||xa-xb||是当前粒子a到b的距离。而选择阈值frac根据迭代次数而变化。当另一粒子b满足||xa-xb||/dm<frac时,认为b成为当前粒子的邻域。
这种办法经过实验,取得较好的应用效果,但是由于要计算所有粒子之间的距离,计算量大,且需要很大的存储空间,所以,该方法一般不经常使用。