博客作业06--图

1.学习总结

1.1图的思维导图

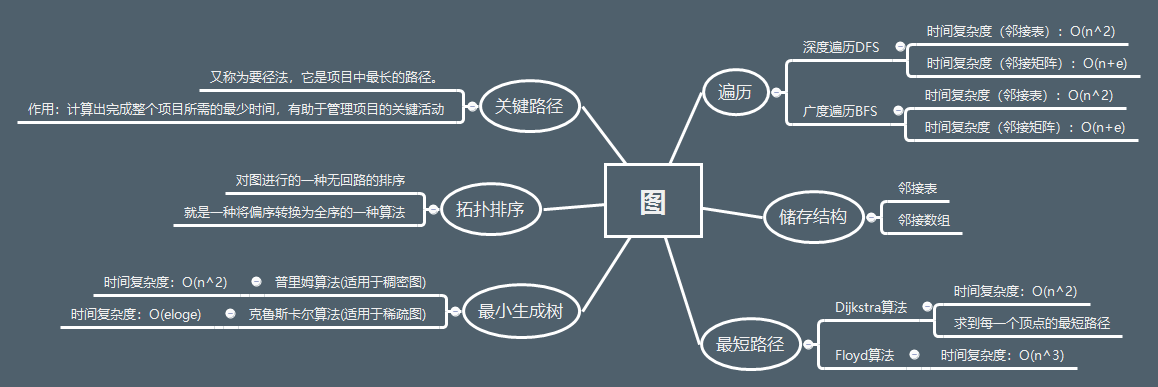
1.2 图结构学习体会

谈谈你对图结构中的几个经典算法学习体会。具体有：

• 深度遍历算法：DFS 在访问图中某一起始顶点 v 后，由 v 出发，访问它的任一邻接顶点 w1；再从 w1 出发，访问与 w1邻 接但还没有访问过的顶点 w2；然后再从 w2 出发，进行类似的访问，… 如此进行下去，直至到达所有的邻接顶点都被访问过的顶点 u 为止。

• 广度遍历算法：其过程类似于层次遍历，借助队列来实现。它的思想是从一个顶点V0开始，辐射状地优先遍历其周围相邻的区域。

• Prim和Kruscal算法：都是无向连通网的最小生成树的算法，Prim算法从一个顶点开始，每次从剩余的顶点中加入一个顶点，该顶点与当前的生成树中的顶点的连边权重最小，直到得到一颗最小生成树；Kruscal算法从权重最小的边开始，每次从不在当前的生成树顶点中选择权重最小的边加入，直到得到一颗最小生成树。Prim算法和Kruskal算法都是贪心算法。Prim算法适用于稠密图，Kruskal算法适用于稀疏图。

• Dijkstra算法：是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

• 拓扑排序算法：将有向图中的顶点以线性方式进行排序。即对于任何连接自顶点u到顶点v的有向边uv，在最后的排序结果中，顶点u总是在顶点v的前面。

2.PTA实验作业

2.1 题目1：7-1 图着色问题

2.2 设计思路

• main()主函数
  判断给的颜色c是否大于给出的顶点数 ，是就输出NO，结束
  建图，输入判断的组数v
  while(v--){
  输入颜色for i=0 to n
  判断颜色是否不同于c给的数量if(!number(A,c,n))，是输出NO
  不是，利用双层循环遍历邻接矩阵
  当相邻顶点颜色相同时 if(A[i]A[j])输出NO，flag=1
  或者当遍历完矩阵还未输出(flag0),则输出YES
  }
• 计算颜色的函数int number(int A[],int c,int n)
  就是一个简单计算颜色种类的函数

2.3 代码截图

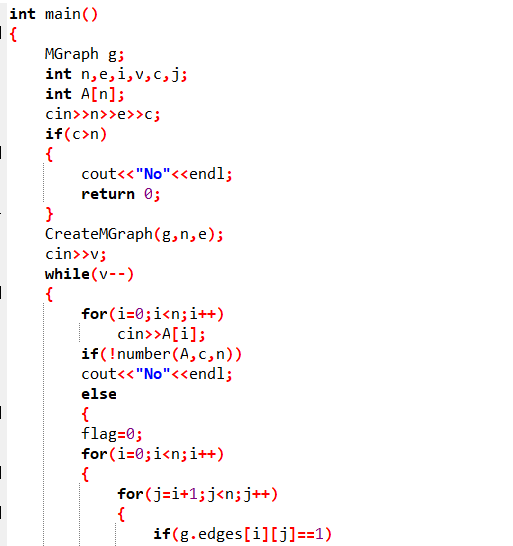
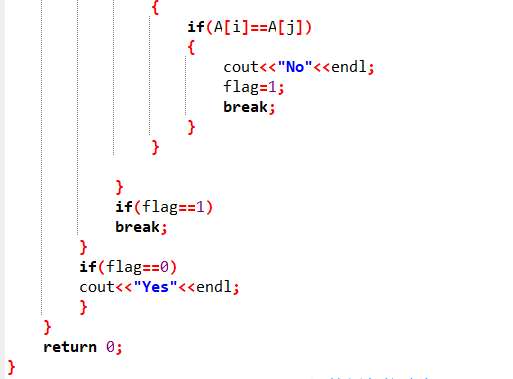
2.4 PTA提交列表说明。

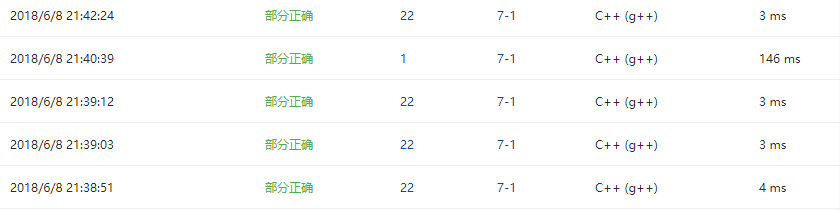
• 图着色的问题，我给的Max的值为20，这就是为什么最大图会段错误的原因，但是我给Max赋值为501的时候，会出现答案错误，我也调试过了，调试了很多次，一直都是错的，所以就放弃了，就部分正确吧。

2.1 题目2：7-2 排座位

2.2 设计思路

• 主函数main()
  建图CreateMGraph(g,n,e);
  while(c--){
  输入要坐在一起的人i，j
  判断俩人的关系，俩人是好朋友或者俩人不认识
  if(g.edges[i-1][j-1]0)和else if(g.edges[i-1][j-1]1)
  如果俩人是死对头，进入找相同朋友的函数Findfriend(g,i,j);
  }
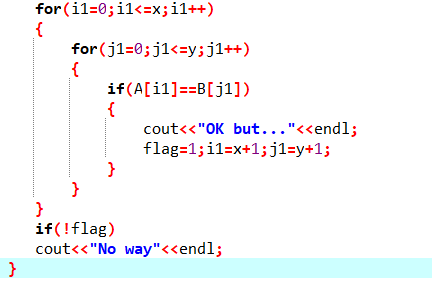
• void Findfriend(MGraph g,int i,int j)找朋友的函数
  分别找i和j的朋友分别放入一个数组A[]和B[]
  在双层循环遍历A[]和B[]数字找是否有共同的朋友
  有就cout<<"OK but..."<<endl;
  没有就cout<<"No way"<<endl;

2.3 代码截图

2.4 PTA提交列表说明。

• 7-2的排座位问题，我用的还是邻接矩阵，但是在最大的图的问题上，还是过不去，我的Max的值不像第一题一样只能20，我给了501，但是还是过不去，我也调试了蛮多次的，和第一题一样一直没正确。

2.1 题目3：7-4 公路村村通

2.2 设计思路

• 主函数main()
  先初始化邻接矩阵
  再是根据输入的顶点数和边的权值构造的邻接矩阵
  然后把数组cost[]赋权值
  输出
• int prime()输出成本最低的函数
  首先for i=0 to n
  {
  在初始化k和min，k放顶点，min放成本最低的路径
  利用循环for j=0 to n
  {
  找出与j成本最低的路径和对应顶点，放入k和min中
  }
  判断是否有这样的顶点if(k!=-1)
  有就把最低成本的路径加入总的sum中
  并且初始化cost[k]，再找出在第k行的成本最低路径
  最后判断是否所有的顶点都遍历到到了
  都遍历到了 返回sum，没有则返回-1
  }

2.3 代码截图

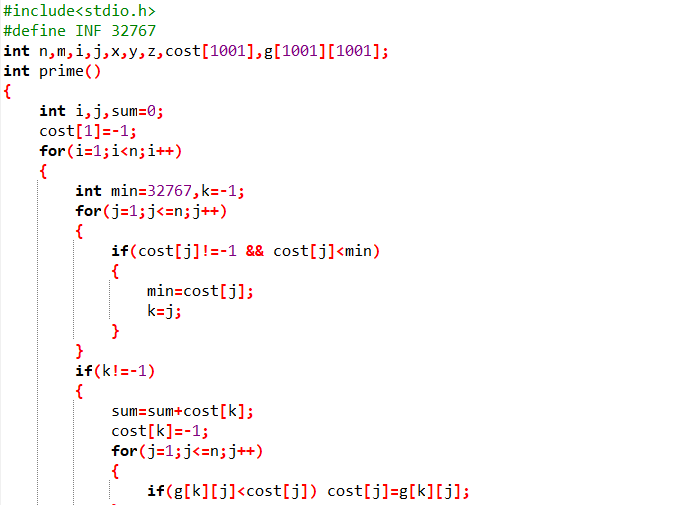
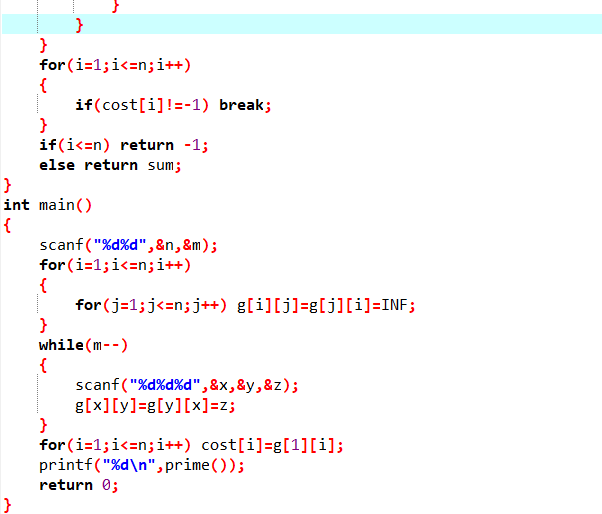
2.4 PTA提交列表说明。

• 一开始想用普里姆算法或者克鲁斯卡尔算法来计算最小生成树，但是按照书上的代码敲完之后发现程序无法运行，只能自己根据概念来写，一开始定义了结构体的二维数组来写，但是部分正确，然后想了想，可以不可以单纯的就用二维数组，然后写了就正确了。

3.截图本周题目集的PTA最后排名

3.1 PTA排名：50

3.2 我的总分：219

4. 阅读代码

bool spfa(int s, int t){
    queue<int>q;
    q.push(s);
    dis[s] = 0;
    inq[s] = 1;
    times[s]++;
    while (!q.empty()){
        int u = q.front(); q.pop();
        inq[u] = 0;
        for (int i = head[u]; i != -1; i = edge[i].next) {
            int v = edge[i].v;
            int w = edge[i].w;
            if (dis[v] > dis[u] + w){
                dis[v] = dis[u] + w;
                if (!inq[v]){
                    inq[v] = 1;
                    q.push(v);
                    times[v]++;
                    if(times[v] > n){
                        return false;
                    }
                }
            }
        }
    }
    return true;
}

• 这是计算最短路径的Spfa算法（队列式判断负权环）
• 适用范围：边权可正可负，单源最短路，还可以判断图中有无负权回路
• 时间复杂度：O(kE)，k非常数，一般认为是所有点的平均入列次数且k一般小于等于2
• 原理：算法思路很简单，将源点加入队列，然后不断从队列中弹出顶点u，遍历u的邻接点v进行松弛更新（若dis[v] < dis[u] + distance[u][v] 则更新dis[v]为dis[u] + distance[u]），更新后如果v点不在队列里则进入队列。
• 这是另一种栈方案判断负权环