程序设计课程总是充满趣味,在学习了判断和循环后就可以编写一些有意思的代码。记得我在初学编程时,老师曾出过一个题目:找出两个整数的最大公约数。当时我在黑板上写下了自己的实现方式:
1 def gcd(a, b): 2 if a == b: 3 return a 4 5 if a < b: 6 a,b = b,a 7 8 result = [i for i in range(1, b + 1) if a % i == 0 and b % i == 0] 9 10 return result.pop()
运行结果是正确的,回到座位上,我为此高兴了两分钟。
后来老师写出了另一个实现:
1 def gcd(a, b): 2 if b == 0: 3 return a 4 else: 5 return gcd(b, a % b)
我的第一反应是:“嗯?”
遗憾的是,我并没有对这段代码深究,只是简单的记住了这种方法,反正都交给计算机计算,何必在乎快慢呢?
后来学了数据结构,知道了用大O评估算法效率,我这才开始重新审视那段寻找最大公约数的代码——它实际上使用了传说中的“辗转相除”,要真正弄清楚来龙去脉,还要从整数说起……
整除和余数
我们都曾经用笨拙的声音从1数到10,这大概是人生中第一次接触数学。稍大一点后,懂得了零的概念,再后来知道了有负数存在……这些美好的记忆都有整数伴随在左右。随着年龄的增长和知识的提升,我们知道了更多关于整数的知识,这其中就包括整除和余数。
欧几里德算式
数学中是以数轴分段的方式定义整除的,如果n是一个正整数,那么可以用n的倍数将数轴分成很多段:

如果将一个整数m放在数轴上,那么m将正好位于qn和(q+1)n之间,其中q也是一个整数:
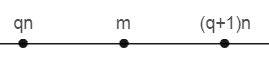
如果m正好是n的整数倍,那么m=qn,否则可以写成m=qn+r形式,qn是在m左侧最近的n的整数倍,r是qn到m的距离。如果把两种情况合并,那么m总是可以写成下面的形式:
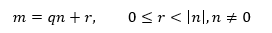
对于特定的n来说,m的表达式唯一的,这种表达式叫做欧几里德算式,也叫做除法算式。
看着挺唬人,其实欧几里德算式有更常见的描述:如果m,n都是整数,并且n≠0,那么总是存在q和r,0≤r<|n|,使得m有唯一的表达式:

其中q是商,r是余数,如果r=0,则称m 能够被n整除,或n能整除m,记作n|m。看来欧几里德算式只不过是从代数上解释了什么是整除,什么是余数。
示例 找出q和r
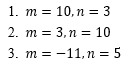
1和2比较简单:
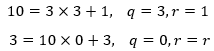
3可能会出点差错:
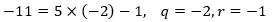
计算机运行的结果:

看来计算机认为是另一种答案:
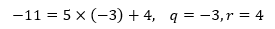
定义终于显现出作用了,在余数的定义中0≤r<|n|,r=-1不满足这个条件,所以正确答案是q=-3,r=4。
整除的性质
整除有一些被人们熟知的性质,如果a,b,c都是整数,则:
1. 如果a|b且a|c,则a|(b+c)
2. 如果a|b,则a|cb
3. 如果a|b且b|c,则a|c
由于0不能作为除数,所以a|b包含的默认条件是a≠0。
此外还有一个推论,如果a,b,c都是整数,当a|b且a|c时,对于任意整数m和n,都有a|(mb+nc)。
除法是乘法的逆运算,这些性质和推论其实都是根据乘法的分配律和结合律推导而来的。
素数
整数的故事中少不了素数,它的另一个名称是质数(prime number),是一种大于1整数。素数是这样定义的:设p是大于1的正整数,如果能整除p的正整数只有p和1,那么p就是一个素数。其中1比较特殊,它不是素数,是单位数。2,3,5,7,11是素数,4,6,8,10,12不是素数。
寻找素数
看起来判断一个整数是否是素数很简单,但这句话仅适用于较小的整数,稍大一点的整数就没那么容易判断了,1234567是否是素数?给你10秒钟时间。
这种复杂的问题还是交给计算机去处理:
1 # 判断a是否是素数 2 def is_prime(a): 3 if a < 2: 4 return False,a 5 elif a == 2: 6 return True,a 7 8 # 用从 2 到 a-1 之间的每个数除以a,看看那个能被整除 9 divisors = [x for x in range(2, a) if a % x == 0] 10 11 return len(divisors) == 0,divisors 12 13 print(is_prime(1234567))
is_prim返回一个包含两个元素的元组,第一个元素回答了a是否是素数,另一个回答了除了1和自身外,a还有哪些约数。
结果显示1234567是不一个素数,除了1和自身外,它还有127和9721两个因数。
寻找素数2.0版
is_prime方法能够正确运行,但仍然有改进的余地。根据欧几里德算式,m=qn,q和n二者此消彼长,它们的平衡点是根号m,这意味着只要判断2到根号m间是否存在能够被m整除的数就可以;此外,一个大于2偶数一定不是素数,所以只需要判断奇数即可。由此得到了判断素数的改进版:
1 import math 2 3 # 判断a是否是素数 4 def is_prime_2(a): 5 if a < 2: 6 return False 7 elif a == 2: 8 return True 9 elif a % 2 == 0: 10 return False 11 12 result = True 13 # 取 math.sqrt(a) 的整数部分 14 end = int(math.sqrt(a)) 15 q = 3 16 while(q <= end): 17 if a % q == 0: 18 result = False 19 break 20 q += 2 21 22 return result
整数分解
我们知道多项式的因式分解,类似地,整数也可以分解,可以将一个正整数写成它的几个约数因子的乘积,这就是整数分解(integer divisorization)。
素因子表达式
大于1的整数分解可以更进一步,使每个因子都是素数。对于每一个大于1的正整数m来说,可以唯一地写成:
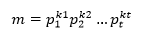
其中pi是能整除m的素数因子,p1<p2<…<pt;ki是pi出现的次数。这种表达式被称为整数m的素因子表达式,对于任意m,它的素因子表达式是独一无二的。将m写素因子表达式的过程叫做素因子分解。
素因子表达也从另一个层面(非素数的层面)定义了素数:如果一个大于1的整数m不是素数,那么m一定能够分解成2个或两个以上素数的乘积,并且这个表达式是唯一的。
示例 写出7、9、20、30的素因子表达式
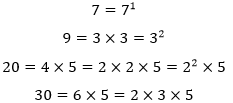
7本身是一个素数,只能整数分解成1×7,但1并不是素数,所以7的素因子表达式就是7本身。
可以使用下面的代码进行整数的素因子分解:
1 # 获取a的所有除1和自身外的约数 2 def get_divisors(a): 3 return [x for x in range(2, a) if a % x == 0] 4 5 # 素因子分解 6 def prim_division(a): 7 if is_prime_2(a): 8 return [a] 9 10 result = [] 11 divisors = get_divisors(a) 12 for divisor in divisors : 13 while True: 14 if a % divisor != 0: 15 break 16 if is_prime_2(divisor): 17 result.append(divisor) 18 a /= divisor 19 else: 20 break 21 22 return result
好了,我们已经知道整数可以素因子分解,但是这有什么用呢?
数学的发展来源于实践,不能用的东西大概也没人去研究。素因子分解的用处还挺多,它可以用来证明素数有无穷个,根号2是无理数,还可以用于密码学、计算复杂理论,甚至用于量子计算等等。接下来就举几个例子,看看素因子分解究竟是怎么使用的。
素数有无穷个吗?
老师:素数有无穷个吗?
同学:当然了!
老师:为什么呢?
同学:没有为什么啊,它当然是无穷的,这还要正明吗?随便给出一个素数,不是很容易的例举出比它更大的素数吗?
老师:但是素数没什么先验的理由必须有无穷多个啊。如果写出一个相当长的,能够绕地球一圈的素数,你能保证一定有一个更大的素数吗?
同学:……
老师:其实你已经回答了,随便给出一个素数,确实能够例举出比它更大的素数,只不过我们需要使用反证法来证明。
假设素数的个数是有限的,那么这些素数都可以用集合的形式列举出来:
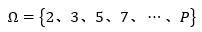
P就是集合中最大的素数。
根据整数的素因子分解,一个大于1的正整数可以分解成若干个素数的乘积,那么存在一个整数M,它等于Ω中所有元素的乘积加1:

M肯定比P更大,P已经被假定是最大的素数,所以M肯定不是素数。素因子表达式告诉我们,M如果不是素数,则一定能够分解成若干个素数的乘积,因为已经假设Ω中包含了所有的素数,所以M也一定能够分解成Ω中若干个元素的乘积。但是现在M除以Ω中的所有元素都会产生余数1,这意味着M只能被M或1整除,所以M也是一个素数,这与“M肯定不是素数”矛盾,因此“素数有无穷个”。
注:“素数有无穷个”这一命题最早的证明出现在古希腊数学家欧几里得 (Euclid) 的《几何原本》上,这一命题也因此被称为了 “欧几里得定理” (Euclid's theorem) 或 “欧几里得第二定理” (Euclid's second theorem)。
根号2为什么“无理”
老师:根号2是一个无理数,它无限不循环,没有尽头。
同学:为什么呢?也许它在绕地球一圈后循环了。
老师:它确实是不循环的,能试试自己证明吗?
同学:还是使用反证法吗?
老师:是的。证明的时候别忘了素因子分解。
假设根号2 是一个有理数,根据有理数的定义,有理数是一个整数a和一个正整数b的比,这样一来,就可以得出:
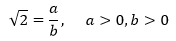
其中a/b不能通分,也就是说a和b是互素的(a和b的公约数只有1)。
现在将等式两侧同时平方:
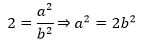
2b2肯定是偶数,所以a2也是偶数,如果a是奇数,则a2也是奇数,所以a只能是偶数,a一定可以素因子分解成:

将a2=2b2等式两侧同时除以2:

a2是偶数,a2/2还是偶数。a2/2= b2所以b2也是偶数,b仍然是偶数,b可以素因子分解成:

现在2|a并且2|b,这和a、b 互素矛盾,所以根号2是无理数。
待续
作者:我是8位的
