经过了长长的铺垫,终于轮到了最大公约数。现在,让我们以全新的视角去审视这个早已熟知的概念。
公约数和最大公约数
除了最大公约数之外,当然还有普通的公约数。
公约数是这样定义的:有两个整数a和b,如果存在另一个能够同时整除a和b的正整数k,那么k就是a和b的公约数,也叫公因数。
当a和b不全为0时,二者公约数中最大的那个就是a和b的最大公约数,也叫最大公因数(greastest common divisor),取英文的首字母表示最大公约数,记作GCD(a,b)。如果GCD(a,b) = 1,则称a,b是互素的,或互质的(relatively prime)。
注:GCD(a, b)中,两个参数谁大谁小没什么关系,通常按照惯例,a ≥ b。
实际上phthon库中有现成的方法:
1 # 打印两个数的最大公约数 2 def paint_gcd(a, b): 3 print('GCD({0}, {1}) = {2}'.format(a, b, math.gcd(a, b))) 4 5 paint_gcd(10, 30) 6 paint_gcd(12, 30) 7 paint_gcd(-6, 14) 8 paint_gcd(17, 93)
打印结果:
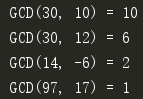
注意到GCD(14, -6)=2,这是因为最大公约数并没有限制a和b是正整数,14和-6都可以被2整除。
公约数定理
公约数存在两个定理,如果d = GCD(a, b),则:
1. 存在整数s和t,使得d = sa + tb,当然,s和t用不着全是正整数;
2. 如果c是a和b的另一个公约数,则c|d。
证明起来比较麻烦,仍然是使用反证法,这里咱们略去证明,但是相信我,这两条定理是正确的。
定理2还产生了一个推论:如果a,b是不全为零的整数,当且仅当满足下面两个条件时,d = GCD(a,b):
1. d|a,且d|b;
2.只要c|a,且c|b,则c|d。
辗转相除
找出a和b的最大公约数似乎很简单,只要找出b的所有约数,这些约数中能被a整除的最大的一个就是二者的最大公约数,这种方法俗称“蛮力法”。对于较为简单的整数,蛮力法很有效:
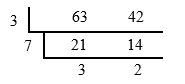
3和2是互素的,GCD(63,42)=3×7=21。
总是使用蛮力没什么意思,更为简单的方法是辗转相除法。代码gcd_2(a, b)已经展示了辗转相除的计算过程:
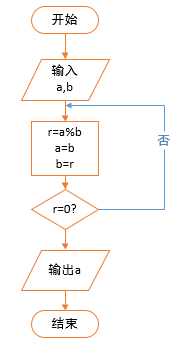
示例 GCD(200, 36) = ?
用36除200,商是5,余数是20,写成欧几里德算式:200=5×36+20
用20除36,商是1,余数是16,36=1×20+16
用16除20,商是1,余数是4, 20=1×16+4
用4除16,商是1,余数是0, 16=4×4+0
GCD(200,36)=4
过程很简单,反复使用余数除以除数,直到能够整除为止,想要理解它生效的原因,恐怕还要从欧几里德算式说起。
设a,b是两个整数,0<b<a,根据欧几里德算式,a可以写成:
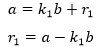
其中k1是正整数,0≤r1<b
根据整除的性质,如果n可以整除a和b,那么n也可以整除r1:
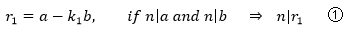
还是同一个n,如果n可以整除b和r1,那么n也可以整除a;

结合①②,a和b的公约数一定是r1的约数,b和r1的公约数也一定是a的约数,且存r1<b<a,这意味着a和b的公约数等价于b和r1的公约数,进而得到GCD(a,b)=GCD(b,r1):
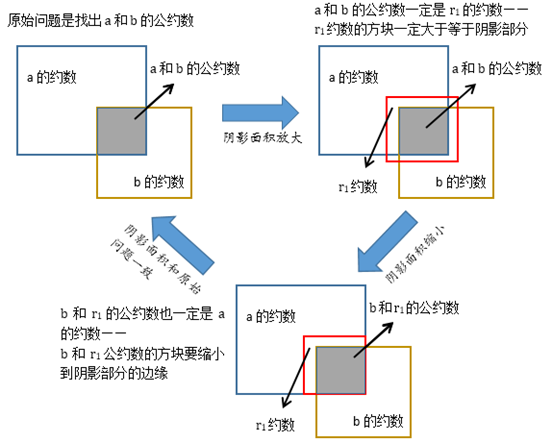
现在用欧几里德算式表示b与r1的关系:
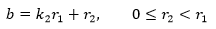
继续表示rn-1和rn的关系:
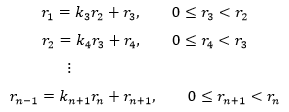
假设第n次是迭代的尽头,即rn-1|rn,rn+1 = 0,由于已经知道了GCD(a,b)=GCD(b,r1),用同样的方式可以知道GCD(b,r1)= GCD(r1,r2),如此继续下去,最终会得到结论:
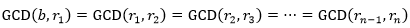
更直观的做法是把欧几里德算式用商和余数表示,用小于b的r1去除以b:

接着往下,反复用除数除以余数:
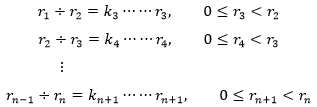
每一次都会得到一个更小的余数,最终余数将达到最小值0,此时没法继续往下除了,迭代结束。
这就是辗转相除的原理,它是用欧几里德算式推导的,所以也叫欧几里德算法。
更相减损
最大公约数还存在另一个定理:
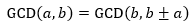
对于这个值得怀疑的等式,只要证明a和b的公约数与b和b±a的公约数相同就可以。根据整除的推论,如果有一个整数c能够同时整除a和b,则对于任意的整数m,n,都有c|(ma+nb):
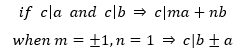
由此得到的结论是,a和b的公约数一定是b±a的约数:
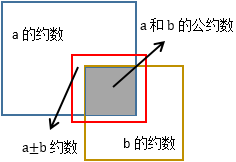
仍然是根据整除的推论:
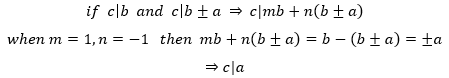
这意味着b和b±a的公约数一定是a的约数:
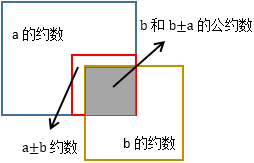
b和b±a的公约数恰好是阴影部分的,所以b和b±a的公约数等价于b和a的公约数,进而得到GCD(a,b)=GCD(b,b±a)。
注:GCD(b,b±a),GCD(b±a,b), GCD(b,a±b)是一回事。
按照定理不断向下进行,最终差值会和较小的数相等,这个相等的数就是最大公约数。
示例: GCD(72,57)=?
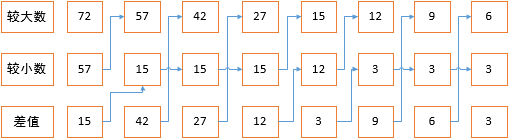
GCD(72,57)=3
这种方法被称为更相减损法。
更相减损法还有一个升级版:
1. 如果a和b都是偶数,就用2分别去除a和b,直到其中一个变成奇数;否则直接跳到2;
2. 使用更相减损不断相减,直到差值和较小数相等;
3. 用步骤1中的若干个2去乘步骤2中最后的差值,结果就是a和b的最大公约数。
由此我们得到了另一个最大公约数的实现方式:
1 # 使用更相减损法求最大公约数 2 def gcd_3(a, b): 3 if a == b: 4 return a 5 elif a < b: 6 a, b = b, a 7 8 # 公约数中2的个数 9 num = 0 10 if a & 1 == 0 and b & 1 == 0: 11 a //= 2 12 b //= 2 13 num += 1 14 15 # 更相减损法 16 r = 0 17 while True: 18 r = abs(a - b) 19 if r == b: 20 break 21 22 a = max(b, r) 23 b = min(b, r) 24 25 return (2 ** num) * r
作者:我是8位的
