书接上文。在坦克寻径的,tank_way中,A*算法每一步搜索都是选择F值最小的节点,步步为营,使得寻径的结果是最优解。在这个过程中,查找最小F值的算法复杂度是O(n),这对于小地图没什么问题,但是对于大地图来说,openlist将会保存大量的节点信息,此时如果每次循环仍然使用O(n)复杂度的算法去查找最小F值就是个非常严重的问题了,这将导致游戏运行缓慢。可以针对这一点行改进,在常数时间内查找到最小F值的节点。
一个现成的数据结构是优先队列,python的heapq模块已经实现了这个功能,它是基于堆优先队列,可以中O(1)时间内返回堆中的最小值。我们用heapq存储openlist中的节点,构建新的坦克寻径代码:
import heapq START, END = (), () # 起点和终点的位置 OBSTRUCTION = 1 # 障碍物标记 class Node: def __init__(self, x, y, parent): self.x = x # 节点的行号 self.y = y # 节点的列号 self.parent = parent # 父节点 self.h = 0 self.g = 0 self.f = 0 def get_G(self): ''' 当前节点到起点的代价 ''' if self.g != 0: return self.g elif self.parent is None: self.g = 0 # 当前节点在parent的垂直或水平方向 elif self.parent.x == self.x or self.parent.y == self.y: self.g = self.parent.get_G() + 10 # 当前节点在parent的斜对角 else: self.g = self.parent.get_G() + 14 return self.g def get_H(self): '''节点到终点的距离估值 ''' if self.h == 0: self.h = self.manhattan(self.x, self.y, END[0], END[1]) * 10 return self.h def get_F(self): ''' 节点的评估值 ''' if self.f == 0: self.f = self.get_G() + self.get_H() return self.f def manhattan(self, from_x, from_y, to_x, to_y): ''' 曼哈顿距离 ''' return abs(to_x - from_x) + abs(to_y - from_y) def __lt__(self, other): ''' 用于堆比较,返回堆中f最小的一个 ''' return self.get_F() < other.get_F() def __eq__(self, other): ''' 判断Node是否相等 ''' return self.x == other.x and self.y == other.y def __ne__(self, other): ''' 判断Node是否不等 ''' return not self.__eq__(other) class Tank_way: ''' 使用A*搜索找到坦克的最短移动路径 ''' def __init__(self, map2d): self.map2d = map2d # 地图数据 self.x_edge, self.y_edge = len(map2d), len(map2d[0]) # 地图边界 # 垂直和水平方向的差向量 self.v_hv = [(-1, 0), (0, 1), (1, 0), (0, -1)] # 斜对角的差向量 self.v_diagonal = [(-1, 1), (1, 1), (1, -1), (-1, -1)] self.openlist = [] # openlist使用基于堆的优先队列 self.closelist = set() self.answer = None def is_in_map(self, x, y): ''' (x, y)是否中地图内 ''' return 0 <= x < self.x_edge and 0 <= y < self.y_edge def in_closelist(self, x, y): ''' (x, y) 方格是否在closeList中 ''' return (x, y) in self.closelist def add_in_openlist(self, node): ''' 将node添加到 openlist ''' heapq.heappush(self.openlist, node) def add_in_closelist(self, node): ''' 将node添加到 closelist ''' self.closelist.add((node.x, node.y)) def pop_min_F(self): ''' 弹出openlist中F值最小的节点 ''' return heapq.heappop(self.openlist) def append_Q(self, P): ''' 找到P周围可以探索的节点,将其加入openlist,并返回这些节点 ''' Q = {} # 将水平或垂直方向的相应方格加入到Q for dir in self.v_hv: x, y = P.x + dir[0], P.y + dir[1] # 如果(x,y)不是障碍物并且不在closelist中,将(x,y)加入到Q if self.is_in_map(x, y) and self.map2d[x][y] != OBSTRUCTION and not self.in_closelist(x, y): node = Node(x, y, P) Q[(x, y)] = node heapq.heappush(self.openlist, node) # 将node同时放入openlist中 # 将斜对角的相应方格加入到Q for dir in self.v_diagonal: x, y = P.x + dir[0], P.y + dir[1] # 如果(x,y)不是障碍物,且(x,y)能够与P联通,且(x,y)不在closelist中,将(x,y)加入到Q if self.is_in_map(x, y) and self.map2d[x][y] != OBSTRUCTION and self.map2d[x][P.y] != OBSTRUCTION and self.map2d[P.x][y] != OBSTRUCTION and not self.in_closelist(x, y): node = Node(x, y, P) Q[(x, y)] = node heapq.heappush(self.openlist, node) # 将node同时放入openlist中 return Q def a_search(self): while self.openlist: # 找到openlist中F值最小的节点作为探索节点 P = self.pop_min_F() # 如果P在closelist中,执行下一次循环 if self.in_closelist(P.x, P.y): continue # P加入closelist self.add_in_closelist(P) # P周围待探索的节点 Q = self.append_Q(P) # Q中没有任何节点,表示该路径一定不是最短路径,重新从openlist中选择 if not Q: continue # 找到了终点, 退出循环 if Q.get(END) is not None: self.answer = Node(END[0], END[1], P) break def start(self): node_start = Node(START[0], START[1], None) self.add_in_openlist(node_start) self.a_search() def paint(self): ''' 打印最短路线 ''' node = self.answer while node is not None: print((node.x, node.y), 'G={0}, H={1}, F={2}'.format(node.g, node.h, node.get_F())) node = node.parent if __name__ == '__main__': map2d = [[0] * 8 for i in range(8)] map2d[5][4] = 1 map2d[5][5] = 1 map2d[4][5] = 1 map2d[3][5] = 1 map2d[2][5] = 1 START, END = (3, 2), (5, 7) a_way = Tank_way(map2d) a_way.start() a_way.paint()
Tank_way_2省略的代码和Tank_way一致。为了让openlist能够返回F值最小值的节点,需要在Node中添加三个额外的方法。对于pop_min_F()而言,不再需要遍历所有节点,仅仅是从堆顶弹出而已,这将大大缩短程序运行的时间。在Tank_way_2中,用append_Q代替了原来来的get_Q(),这是因为不再需要用Q中的节点和openlist中的节点相比较,仅仅是将Q中的节点添加到openlist中。这样做虽然会使得openlist中存在一些重复节点,不过没关系,对于有相同标记的节点,F值小的那个总是最先弹出,一旦弹出就会加入到closelist中,这意味着当该标记的节点再次弹出时,将不会被使用,也就是说,如果同一个标记的节点被计算了多次F值,总是能够确保使用F值最小的那个,并丢弃其它的。
再战觐天宝匣
基于盲目策略的广度优先收索无法有效完成4阶以上的拼图(可参考搜索的策略(3)——觐天宝匣上的拼图),在理解了A*搜索后,可以用这种启发性策略再次挑战觐天宝匣的拼图。
设计评估函数
如果将拼图的每一次移动看作“一步”,只要能定义出离评估函数和代价函数,就可以像坦克寻径一样使用A*搜索寻找拼图的复原步骤。
我们将g(n)定义为从起点移动到某个状态的步数;h(n)是当前状态到复原状态的距离估值,它用所有碎片的曼哈顿距离之和表示。以3×3的拼图为例,假设拼图的某个状态和复原状态是:

左图中,3号碎片的位置是(2,0),它在复原状态的位置是(1,0),则3号碎片的曼哈顿距离是|2-1|+|0-0|=1。同理,5号碎片的曼哈顿距离是|0-1|+|1-2|=2。左图距复原状态的曼哈顿距离是所有碎片的曼哈顿距离之和:

其中Dn表示第n个碎片的曼哈顿距离,图眼的编号是8。
复原拼图
有了g和h就可以开始复原拼图,复原过程和坦克的寻路类似。从拼图的初始状态开始,第一步可以向三个方向探测,从而产生三种状态:
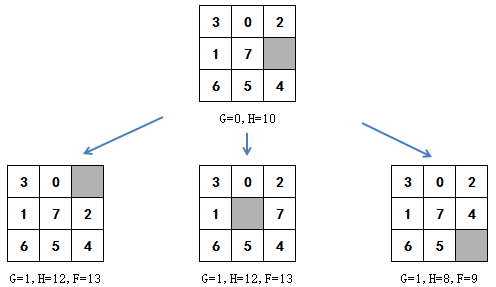
此后每一步都选择最小的F值继续探索,如果F值相同,则选择最后加入openlist中的一个:
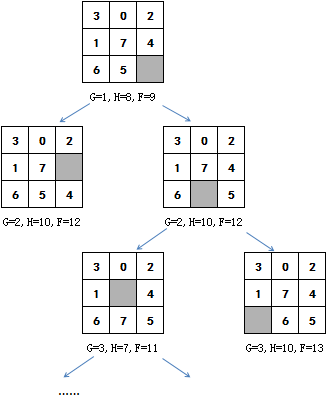
最终的复原步骤如图:
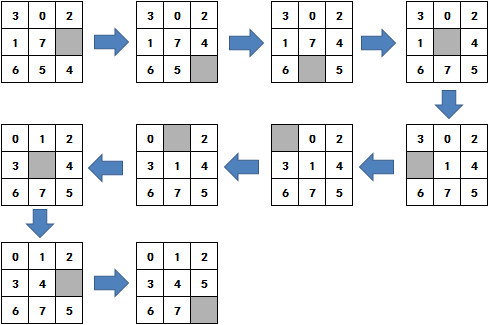
实现A*搜索
拼图的实现和坦克寻径类似,完整代码如下:
import random import copy import heapq IMG_END = [] # 拼图的复原状态 EYE_VAL = ' ' # 图眼的值 DIST = {} def get_hash_value(img): ''' 获取img的哈希值 ''' return hash(str(img)) class Node: def __init__(self, img, x=0, y=0, parent=None): self.img = img # 当前拼图 self.x, self.y = x, y # 图眼在img中的位置 self.parent = parent # 父节点 self.hash_value = get_hash_value(img) # Node的哈希值 self.h = 0 self.g = 0 self.f = 0 def get_G(self): ''' 当前节点到起点的代价 ''' if self.g != 0: return self.g elif self.parent is None: self.g = 0 else: self.g = self.parent.get_G() + 1 return self.g def get_H(self): ''' 节点到终点的距离估值 ''' if self.h == 0: self.h = self.manhattan() return self.h def get_F(self): ''' 节点的评估值 ''' if self.f == 0: self.f = self.get_G() + self.get_H() # self.f = self.get_H() return self.f def manhattan(self): '' '当前拼图到复原状态的距离 ''' d = DIST.get(self.hash_value) if d is not None: return d dist = 0 x_end, y_end = 0, 0 # img_end 中某一个碎片的位置 n = len(self.img) for x, row in enumerate(self.img): for y, piece in enumerate(row): if piece == IMG_END[x][y]: continue # 计算piece碎片在img_end中的位置 if piece == EYE_VAL: x_end = n - 1 y_end = n - 1 else: x_end = piece // n y_end = piece - n * x_end dist += abs(x - x_end) + abs(y - y_end) DIST[self.hash_value] = dist return dist def __lt__(self, other): ''' 用于堆比较,返回堆中f最小的一个 ''' return self.get_F() < other.get_F() def __eq__(self, other): ''' 判断Node是否相等 ''' return self.img.hash_value == other.img.hash_value def __ne__(self, other): ''' 判断Node是否不等 ''' return not self.__eq__(other) def __hash__(self): return self.hash_value class JigsawPuzzle_A: ''' 用A*搜索复原拼图 ''' def __init__(self, level=1, img_start=None): self.level = level # 难度系数 self.n = len(IMG_END) # 拼图的维度 self.end_hash_value = get_hash_value(IMG_END) # 复原状态的哈希值 # “图眼”移动的方向, 上、左、下、右 self.v_move = [(0, 1), (-1, 0), (0, -1), (1, 0)] # 设置拼图的初始状态和图眼的位置 if img_start is not None: self.img_start = img_start self.eye_x, self.eye_y = self.search_eye(img_start) else: self.img_start, self.eye_x, self.eye_y = self.confuse() self.openlist = [] self.closelist = set() # 拼图复原步骤 self.answer = None def confuse(self): ''' 创建一个n*n的拼图,返回打乱状态和图眼位置 ''' # 拼图的初始状态 img_start = copy.deepcopy(IMG_END) from_x, from_y = self.search_eye(IMG_END) to_x, to_y = from_x, from_y # 将图眼随机移动 n * n * level次 for i in range(self.n * self.n * self.level): # 选择一个随机方向 v_x, v_y = random.choice(self.v_move) to_x, to_y = from_x + v_x, from_y + v_y if self.enable(to_x, to_y): # 向选择的随机方向移动 self.move(img_start, from_x, from_y, to_x, to_y) from_x, from_y = to_x, to_y else: to_x, to_y = from_x, from_y return img_start, to_x, to_y def search_eye(self, img): ''' 找到img中图眼的位置 ''' # “图眼”的值是eye_val,打乱顺序后需要寻找到图眼的位置 for x in range(self.n): for y in range(self.n): if EYE_VAL == img[x][y]: return x, y def in_closelist(self, node): ''' node 是否在closelist中 ''' return node.hash_value in self.closelist def add_in_openlist(self, node): ''' node节点加入openlist ''' heapq.heappush(self.openlist, node) def add_in_closelist(self, node): ''' node节点加入closelist ''' self.closelist.add(node.hash_value) def pop_min_F(self): ''' 找到openlist中F值最小的节点 ''' return heapq.heappop(self.openlist) def enable(self, to_x, to_y): ''' 图眼是否能够移动到x,y的位置 ''' return 0 <= to_x < self.n and 0 <= to_y < self.n def move(self, img, from_x, from_y, to_x, to_y): ''' 将图眼从from_x, from_y移动到to_x, to_y ''' img[from_x][from_y], img[to_x][to_y] = img[to_x][to_y], img[from_x][from_y] def append_Q(self, P): ''' 找到P周围可以探索的节点,将其加入openlist,并返回这些节点 ''' Q = {} for v_x, v_y in self.v_move: to_x, to_y = P.x + v_x, P.y + v_y # 检验是否可以向to_x, to_y方向移动 if not self.enable(to_x, to_y): continue curr_img = copy.deepcopy(P.img) self.move(curr_img, P.x, P.y, to_x, to_y) # 如果node是不在closelist中,把node添加到Q中 if not self.in_closelist(Node(curr_img)): node = Node(curr_img, x=to_x, y=to_y, parent=P) Q[node.hash_value] = node self.add_in_openlist(node) return Q def a_search(self): ''' A*搜索拼图的解 ''' while self.openlist: # 找到openlist中F值最小的节点作为探索节点 P = self.pop_min_F() # 如果P在closelist中,执行下一次循环 if self.in_closelist(P): continue # P加入closelist self.add_in_closelist(P) # P周围待探索的节点 Q = self.append_Q(P) # Q中没有任何节点,表示该路径一定不是最短路径,重新从openlist中选择 if not Q: continue # 找到了终点, 退出循环 if Q.get(self.end_hash_value) is not None: self.answer = Node(IMG_END, parent=P) break def start(self): if self.img_start == IMG_END: print('start = end') return node_start = Node(img=self.img_start, x=self.eye_x, y=self.eye_y) self.add_in_openlist(node_start) self.a_search() def display(self): if self.answer is None: print('No answer') node = self.answer while node is not None: print(node.img) node = node.parent def create_img_end(n): ''' 创建一个n*n的拼图,将右下角的碎片图指定为图眼 ''' img = [] for i in range(n): img.append(list(range(n * i, n * i + n))) img[n - 1][n - 1] = EYE_VAL return img if __name__ == '__main__': n = 9 IMG_END = create_img_end(n) # img_start = [[3, 0, 2], [1, 7, EYE_VAL], [6, 5, 4]] jigsaw = JigsawPuzzle_A(level=5) print('start=', jigsaw.img_start, ',eye =', (jigsaw.eye_y, jigsaw.eye_x)) jigsaw.start() jigsaw.display()
JigsawPuzzle_A中额外设置了难度系数,level的值越大,复原拼图越困难。对于一个拼图来说,level=5已经足以打乱顺序:

九九拼图的复原已经非人力所能解决。JigsawPuzzle_A可以快速复原任意难度的4×4拼图,对于更高阶的拼图,即使是A*搜索,面对的搜索数量依然十分庞大,需要耗费相当长的时间,只有level=1的时候 9×9拼图才能快速得到结果。
作者:我是8位的
