在现实世界中,我们的生活受到大量网络的支配。网络流可以表示很多模型,比如管道中的石油、高压线中电流,或者计算机网络中的数据。网络流也可以解决很多问题,比如如何进行道路交通管控,以便有效地缓解早高峰的拥堵;在物流网运输中,在满足供需关系的同时,怎样使渠道成本最低;在轰炸机执行轰炸任务时,怎样才能给敌军补给线造成更严重的打击。这些问题都有现成的网络流算法,别再以为网络流仅仅是网络中的比特流。
网络和流网络
简单地说,流网络是一种有加权边的有向图。在数学中,网络是这样定义的:网络(Networks)G=(V,E,s,t,C) 是一个五元组。其中(V, E)是一个有向图,V是顶点的集合,E是边的集合,它们都是非负实数集;s和t是(V, E)中的两个不同顶点;s的入度为0(没有指向s的边),是G的源点(source);t的出度为0(没有边从t发出),是G的汇点(sink);C是容量函数,对于(V, E)中的任意有向边 a,称 C(a)是边 a 的容量(capacity)。对于仅有一个指定的原点s和指定的汇点t的网络,称为st-网。
实际上网络的概念相当直白,我们以一个简单的物理模型直观地解释网络。假设有一组联通的输油管道,管道连接处的中转站设有控制开关。这组管道的源头是一个油田,汇点是一个炼油厂,石油从油田流出,最终汇入炼油厂:
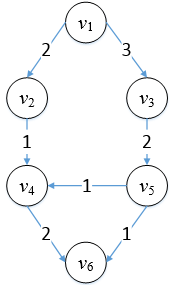
图1
图1是一个带有加权边的有向图,也是一个典型的st-网。其中v1代表油田,是源点s,v6代表炼油厂,是汇点t,其它顶点代表中转站;每条边代表一个输油管道,边上的数字是管道的容量,数字越大,管道越粗,单位时间能够流过管道的油量也越大。把这些信息映射到网络的定义,那么:
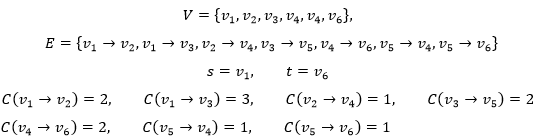
输油管道会定期保养,不会产生漏油的情况,更不会平白无故生出石油,因此所有边的容量都是正值,这种所有容量都是正数的st-网称为流网络(Flow Network)。对于流网络来说,顶点没有容量。作为一个枢纽,中转站并不存储石油,只负责通过开关控制石油流动的方向;同样,石油只是流过输油管道,并不会在管道中积累或聚集。
流、网络流和网络流的值
石油将在流网络的管道中流动,这些流动的石油就是流网络中的流。很显然,管道中的石油不能超过管道的宽度。在流网络模型上,流可以看作另一组隐藏的边权值,称为边流。流网络有多条边,当然也有多个流。对于输油网的各个中转站来说,由于没有存储功能,因此流入的中转站的石油等于流出中转站的石油。
这些特点归可以纳出流的定义:一个网络G=(V,E,s,t,C)是流网络,它的一个流是一个函数f,这个函数满足2个条件:
(1)容量限制,对于任意的边 a, 0≤f(a)≤C(a),即边的流不会大于该边的容量。
(2)守恒定律,对于任意内部顶点v ,进入顶点的流量等于从该顶点发出的流量,简称“流入等于流出”。
作为流网络的源头,没有流入原点的边;类似地,也没有从汇点流出的边。假设石油从油田到炼油厂的传输过程中没有任何损失,那么石油从源点的流出量等于汇点的流入量。
为了方便地展示网络中的流,我们先对网络的表示加以改进,用边的宽度表示边的容量,使宽度和容量成正比,管道越宽,容量也越大:
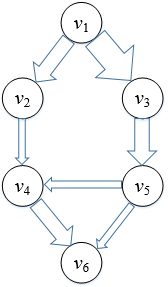
图2
当石油流过输油管道时,管道将被填充。我们以实心箭头代表石油,填充原来的管道,流的值和管道的容量成正比:
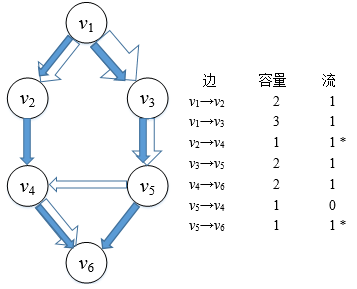
图3
在图3中,边v2→v4的容量是1,流也是1,此时我们说这条边是满边,用星号表示满边的流值。边v1→v3的容量是3,流是1,说明这条管道并没有得到充分利用,实心箭头填充了管道1/3的空间。边v5→v4的容量是1,流是0,v5→v4处的开关是闭合的,这条管道处于闲置状态。
图3也展示了从源点到汇点的所有流,因此我们也称图3是一个网络流(network-flows)。
流网络、流、网络流,看起来极为相似,很多资料中也互相混用,但三者还是有所区别。网络流是指所有容量都是正数的st-网;流代表个体,特指某一条边上的流量;网络流代表整体,表示流网络上所有流的集合。此外,网络流还有另一个含义,指用流网络的模型找出解决问题的方法。网络流的含义究竟是集合还是方法,需要根据具体的上下文而定。通常来讲,这些概念在实际问题中非常直白,不必太过纠结。
源点的流出量或汇点的流入量称为网络流的值。在图8.3中,网络流的值是:

最大流
图3所示的网络流的值是2,在这个网络中是否存在另外一个值更大的网络流?
既然网络流的值取决于源点的流出量会或汇点的流入量,那么只要使源点流出边的容量或汇点流入边的容量充分得到利用,就能能够取得网络流的最大值。这似乎只是一个简单的加法和比较运算:

只要尽全力填满油田的输油管道就好了:
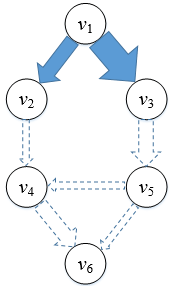
图4
遗憾的是,这种方式是错误的,它忽略了其它边的容量,破坏了“流入等于流出”的守恒定律。以图4为例,C(v2→v4)和C(v3→v5)的总容量是3,不足以容纳5个单位的石油。换句话说,下游的容量制约了上游的生产力。
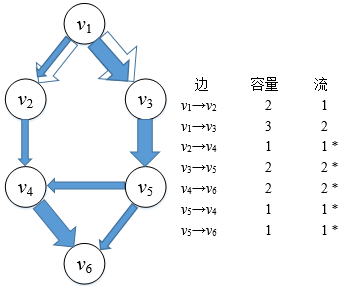
油田通过两条管道输出石油,其中的一条路径是v1→v2→v4→v6,当f(v1→v2)=1时,v2→v4是满边,它已经被充分利用,根据守恒定律,这条路径上的总流量是1。类似地,另一条路径v1→v3→v5→v6的总流量也是1。别忘了,我们在v5→v4处还有一个开关,打开这个开关,会得到另一条路径v1→v3→v5→v4→v6,这将使更多的管道得到充分利用,此时得到了网络中的最大流,Fmax=3:
基本数据结构
以下是网络流的基本数据结构,后续章节将反复用到并扩充这个结构:
1 class Edge(): 2 ''' 边 ''' 3 def __init__(self, v_from:int, v_to:int, cap:int, flow=0): 4 ''' 5 :param v_from: 起点 6 :param v_to: 终点 7 :param cap: 容量 8 :param flow: 流 9 ''' 10 self.v_from, self.v_to = v_from, v_to 11 self.cap, self.flow = cap, flow 12 13 def is_from(self, v): 14 ''' 是否是v顶点的流入边 ''' 15 return self.v_from == v 16 17 def is_to(self, v): 18 ''' 是否是v顶点的流出边 ''' 19 return self.v_to == v 20 21 def __str__(self): 22 return str(self.v_from) + ' → ' + str(self.v_to) 23 24 class Network(): 25 ''' st-网络 ''' 26 def __init__(self, V:list, E:list, s:int, t:int): 27 ''' 28 :param V: 顶点集 29 :param E: 边集 30 :param s: 原点 31 :param e: 汇点 32 :return: 33 ''' 34 self.V, self.E, self.s, self.t = V, E, s, t 35 36 def get_from_edges(self, v): 37 ''' 38 获取顶点的流入边 39 :param v: 顶点值 40 :return: 顶点的流入边list 41 ''' 42 return [edge for edge in self.E if edge.is_from(v)] 43 44 def get_to_edges(self, v): 45 ''' 46 获取顶点的流出边 47 :param v: 顶点值 48 :return: 顶点的流出边list 49 ''' 50 return [edge for edge in self.E if edge.is_to(v)] 51 52 def flows_from(self, v): 53 '''v顶点的流入量 ''' 54 edges = self.get_from_edges(v) # v的流入边 55 return sum([e.flow for e in edges]) 56 57 def flows_to(self, v): 58 '''v顶点的流出量 ''' 59 edges = self.get_to_edges(v) # v的流出边 60 return sum([e.flow for e in edges]) 61 62 def check(self, s, t): 63 ''' 源点的流出是否等于汇点的流入 64 :param s: 源点 65 :param t: 汇点 66 :return: s流出 = t流入,返回true 67 ''' 68 return self.flows_to(s) == self.flows_from(t) 69 70 def display(self): 71 print('%-10s%-8s%-8s' % ('边', '容量', '流')) 72 for e in self.E: 73 print('%-10s%-10s%-8s' % (e, e.cap, e.flow)) 74 75 V = [1, 2, 3, 4, 5, 6] 76 E = [Edge(1, 2, 2), Edge(1, 3, 3), Edge(2, 4, 1), Edge(3, 5, 2), 77 Edge(4, 6, 2), Edge(5, 4, 1), Edge(5, 6, 1)] 78 s, t = 1, 6 79 G = Network(V, E, s, t) 80 G.display()

作者:我是8位的
