网络流(3)——找到最小st-剪切

　　在大规模战争中，后勤补给是重中之重，为了尽最大可能满足前线的物资消耗，后勤部队必然要充分利用每条运输网。与此同时，交战双方也想要以最小的代价切断敌军的补给，从而使敌军处于孤立无援的境地。在古今中外的各种重大战役中，上演了一幕幕补给线上的攻防战。

甲军的运输路线

　　假设甲、乙两军正在交战，图8.17是甲军的补给运输网，其中t是甲军的前沿阵地，s是后勤大营，每条边是一条公路，边上的数字代表公路的宽度。

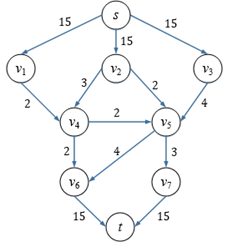
　　如果甲军想要尽最大努力供应前线的消耗，应该怎样设计运输路线？

　　这个问题很容易规约成网络流模型，使用下面的代码可以直接计算出结果。

import network_flow as nf

V = [0, 1, 2, 3, 4, 5, 6, 7, 8]
E = [nf.Edge(0, 1, 15), nf.Edge(0, 2, 15), nf.Edge(0, 3, 15), nf.Edge(1, 4, 2), nf.Edge(2, 4, 3),
     nf.Edge(2, 5, 2), nf.Edge(3, 5, 4), nf.Edge(4, 5, 2), nf.Edge(4, 6, 2), nf.Edge(5, 6, 4),
     nf.Edge(5, 7, 3), nf.Edge(6, 8, 15), nf.Edge(7, 8, 15)]
s, t = 0, 8
G = nf.Network(V, E, s, t)
ford_fullkerson = nf.FordFulkerson(G)
ford_fullkerson.start()
ford_fullkerson.display()
X, Y, st_cut = ford_fullkerson.min_st_cut()
ford_fullkerson.display_st_cut(X, Y, st_cut)

　　（network_flow参考上一章的相关代码）运行结果对应的网络流：

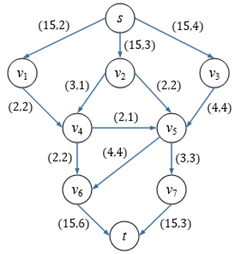
乙军的轰炸目标

　　甲军想要充分利用每条公路，乙军的目的正好相反，是破坏公路网，使乙军的战斗部队处于孤立无援的境地。乙军打算组织一次针对甲军补给线的战略轰炸，由于甲军在每个节点都部署了大量防空武器，因此需要绕过节点，直接轰炸防御薄弱的公路。假设炸掉容量为1的公路需要n颗炸弹，破坏的公路容量和投掷的炸弹数成正比，怎样设计轰炸目标才能以最小的代价完全破坏敌军的补给线？

　　一个方案是炸毁直接通向汇点的公路，但由于连接汇点的两条公路太宽，完全破坏需要30n的炸弹，这显然不是最小代价。如果换个地点，假设轰炸的是v₅→v₇，那么只需要3n的炸弹就可以使宽敞的v₇→t沦为摆设。为了设计这种轰炸方案，需要理解最小st-剪切的概念。

8.3.3 最小st-剪切

　　设计成本最低的轰炸方案是我们的目标，直接寻找起来比较困难，幸而这个目标与网络的最小剪切有密切关系。

　　一个流网络的顶点可以划分成两个不相交的集合X和Y，源点s和汇点t分属于这两个集合，连接X和Y的边称为这个流网络的st-剪切（st-cut，也称为截、割或切割）。我们用浅色圆圈表示包含源点的集合X，深色圆圈表示包含汇点的集合Y，这样就很容易看出一个流网络的st-剪切：

　　既然st-剪切是边的集合，那么集合中边的容量之和就是st-剪切的容量。一个流网络有很多种不同的st-剪切，其中容量最小的一个就是最小st-剪切。

　　st-剪切包含了所有源点到汇点的通道，一个显而易见的结论是：st-剪切的流值等于这个网络流的值。更进一步，任何网络流的值都不会超过st-剪切的容量，这也意味着st-剪切代表着流网络的瓶颈，最小st-剪切的容量不会小于最大流的值，这个定理称为最大流-最小剪切定理。该定理也可以反过来表述：网络流的值最大不会大于任意一个给定的st-剪切的容量。当X只包含源点或Y只包含汇点时，最大流-最小剪切定理最为直观。

　　最小st-剪切代表补给线上最难走或最重要的路段，只要破坏这些路段，就能以最小的代价掐断敌军的补给，即使只破坏了一部分，也能有效降低敌军的补给能力。既然最小st-剪切和最大流存在关联关系，我们就可以在寻找最大流时顺带找出最小st-剪切，这仍然需要使用残存网。在残存网中，将源点和从源点出发可以到达的顶点看作集合X，剩下的顶点看作集合Y，对于边v→w，如果满足v属于X，w属于Y，那么v→w就是最小st-剪切中的一条边。

　　以下图为例，在残存网中源点能够到达的顶点只有v₃，原网络的最小st-剪切是：

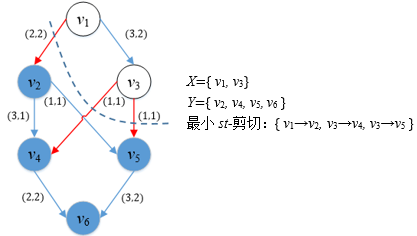
　　可以根据这种思路在FordFulkerson中添加寻找最小st-剪切的实现。

class FordFulkerson():
    def __init__(self, G:Network):
        self.G = G
        self.max_flow = 0  # 最大流
    …… （省略部分参考上一章的相关代码）
    def min_st_cut(self):
        ''' 找到最小st-剪切 '''
        X = [self.G.s] # st-剪切的X集合
        stack = [self.G.s]
        while len(stack) > 0:
            v = stack.pop()
            for e in  self.G.edges_from(v): # 所有从v顶点流出的边
                if e.w != self.G.t and e.w not in X and  e.residual_cap_to(e.w) > 0:
                    X.append(e.w)
                    stack.append(e.w)
        Y = list(set(self.G.V) - set(X)) # st-剪切的X集合
        st_cut = [e for e in self.G.E if e.v in X and e.w in Y] # 连接X和Y的边
        return X, Y, st_cut

    def display_st_cut(self, X, Y, st_cut):
        print('X={0}, Y={1}'.format(X, Y))
        print('st-cut={}'.format([str(e) for e in st_cut]))

　　min_st_cut使用深度优先搜索寻找最小st-剪切。由于这种方法需要借助残存网，因此在使用min_st_cut前需要首先执行一次计算最大流的操作。现在可以计算出乙军的轰炸目标了：

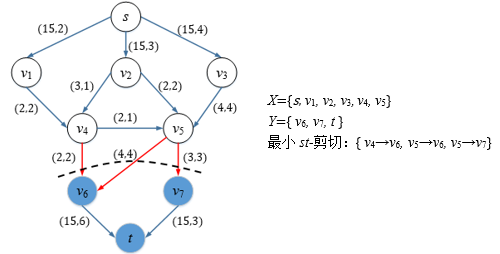
姜子牙的押粮官

　　在《封神演义》中，姜子牙经过金台拜将之后，担任“扫荡成汤天宝大元帅”一职，代武王伐纣。率领六十万西岐大军浩浩荡荡，东进朝歌。所谓“三军未动，粮草先行”，在临行前，姜子牙任命了四个先锋官的同时，又任命了杨戬、土行孙、郑伦三个押粮官。

　　押粮前必先征粮，单从一个地方征粮恐怕不足以支持一场灭国战争，假设下图是西岐的粮道。

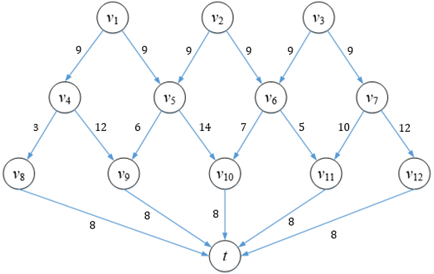
　　边的容量代表粮道的运力，杨戬、土行孙、郑伦分别从三v₁、v₂、v₃个征粮地同时出发，将粮草运往唯一的前沿阵地t，由于运粮过程中十分安全，所以三人可以在每个节点处合兵或分兵，怎样行进才能使粮道发挥出最大运力呢？

多个源点与多个汇点

　　问题可以规约成典型的最大流问题，但与之前介绍的st-网络不同，粮道图中有多个源点（或者说没有源点），如此一来将会对最大流的相关算法造成影响，怎么办呢？

　　其实很简单，在三个源点前再加入一个超级源点，这样一来v₁、v₂、v₃就变成了普通的节点，它们也符合守恒定律，原网络也转换成了st-网：

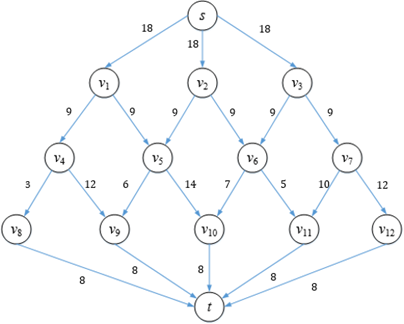
　　与此类似，也可以通过建立一个超级汇点来处理多个汇点的情况。

粮道的最大运力

　　有了超级节点后，只要把初始数据输入交给计算机就可以了。

import network_flow as nf

V = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]
E = [nf.Edge(0, 1, 18), nf.Edge(0, 2, 18), nf.Edge(0, 3, 18), nf.Edge(1, 4, 9),
     nf.Edge(1, 5, 9), nf.Edge(2, 5, 9), nf.Edge(2, 6, 9), nf.Edge(3, 6, 9),
     nf.Edge(3, 7, 9), nf.Edge(4, 8, 3), nf.Edge(4, 9, 12), nf.Edge(5, 9, 6),
     nf.Edge(5, 10, 14), nf.Edge(6, 10, 7), nf.Edge(6, 11, 5), nf.Edge(7, 11, 10),
     nf.Edge(7, 12, 12), nf.Edge(8, 13, 8), nf.Edge(9, 13, 8), nf.Edge(10, 13, 8),
     nf.Edge(11, 13, 8), nf.Edge(12, 13, 8)]
s, t = 0, 13
G = nf.Network(V, E, s, t)
ford_fullkerson = nf.FordFulkerson(G)
ford_fullkerson.start()
ford_fullkerson.display()

　　最大流是33，下图是根据程序运行结果映射的网络流。

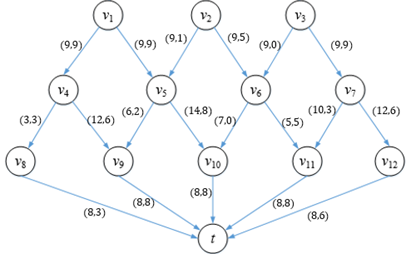
　　最大流是确定的，但押粮路线并不是唯一的，最大流算法和边的输入顺序都会对它产生影响。对于增广路径最大流算法来说，寻找增广路径的算法也会影响最终的押粮路线。

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”