多变量微积分笔记14——保守场和独立路径

　　场论理论包括多种形式，比如简单的向量场，而梯度场则是由数量场所得到的矢量场，它的定义与坐标系的选择无关。梯度场在微分学、积分学以及算子的定义方面起着重要的作用。梯度场在物理学中也称为保守场，这来源于能量守恒定律。

梯度场与势函数

　　f(x, y)是关于x和y的函数，如果存在向量场F = ▽f，也就是向量场F是f 的梯度，那么称F是梯度场，f是梯度场F的势函数。

线积分的基本定理

　　单变量微积分的基本定理告诉我们，对原函数的导数积分会得到原函数。相应地，线积分的基本定理是这样描述的：如果对一个函数的梯度做线积分，就能得到原函数。

　　线积分的基本定理告诉我们，如果沿一条曲线对一个函数f的梯度做积分，即对一个梯度场做积分，计算结果将会是f在P₁点的值减去f在P₀点的值：

　　需要注意的是，上式仅在梯度场中成立（下一章将具体介绍如何确定一个场是否是梯度场）。

　　根链全微分(可参考《多变量微积分4——全微分与链式法则》)：

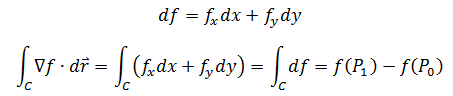
　　这就和单变量微积分的基本定理一致。

定理的证明

　　将x和y参数化，C是在 t 时间内移动的轨迹：

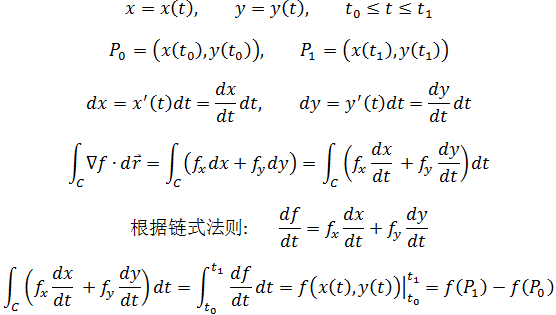
定理的应用

　　在上一章《线积分》中有这样一个示例：

　　如下图所示，在向量场F = yi + xj中，质点移动的轨迹是C₁→C₂→C₃，三段轨迹围成了闭合的扇形，扇形的半径是1，弧度是 π/4，求力场中对质点的总功。

 

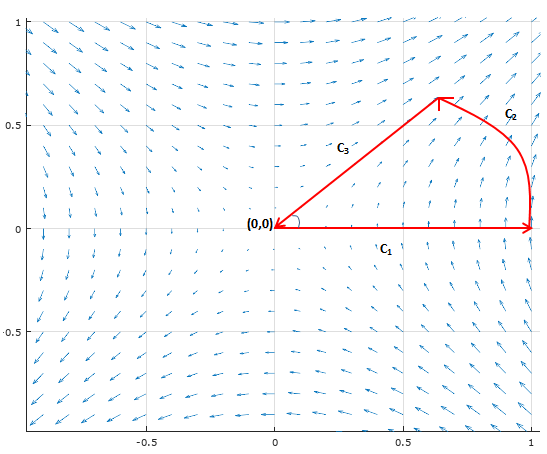
　　上一章花了比较大的力气计算总功，有了基本定理，就可以使计算简化。很容易看出，F = yi + xj是一个梯度场，它的势函数是f = xy，所以：

 

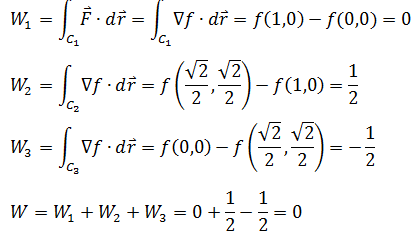
独立路径

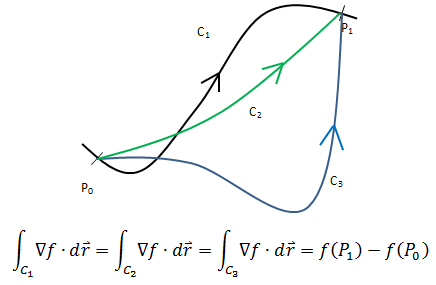
　　线积分基本定理的一个重要结论是独立路径：在梯度场中，如果需要计算一个线积分，无论怎样的路径，积分值都只跟起点和终点的值有关。在梯度场中，下图三条路径的线积分是等价的。

　　对于闭合区间，可以用一个新的积分符号表示，以此强调闭合：

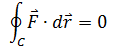
闭合的独立路径

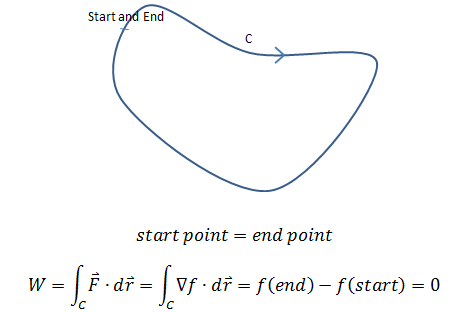
　　在保守场中，如果C是闭合曲线，那么沿C所做的功是0；相反，如果不是保守场，那么一定存在某个地方，沿着闭合曲线所做的功不为0。反过来说，如果在一个向量场中，沿着某条闭合曲线做的功为0，这并不足以说明这个向量场是保守场，还必须强调是任意闭合曲线。

综合示例

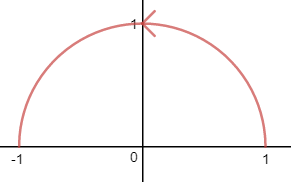
　　梯度场的势函数是f(x,y) = x⁵ + 3xy³，质点运动的轨迹C是半径为1的半圆，计算C在梯度场中的线积分。

　　尝试使用3中方法。

　　1.根据线积分基本定理：

 

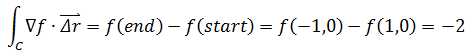
　　2.根据独立路径，下面两个曲线的线积分相等：

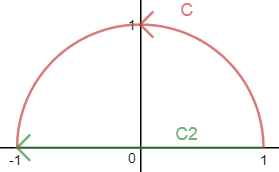
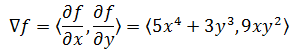
　　在直线轨迹中，y = 0，dy = 0

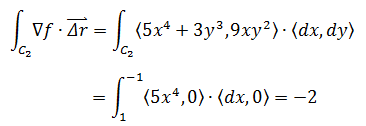
　　3.使x和y参数化：

---

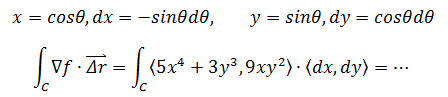
作者：我是8位的

出处：http://www.cnblogs.com/bigmonkey

本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

扫描二维码关注公众号“我是8位的”