旋度
场向量的旋度衡量的是运动的旋转部分,它表达的是在给定点上扭转程度的大小,用数学符号表示就是:

旋度的大小表示扭转程度,正负表示旋转是顺时针还是逆时针。由上一章可知,在保守中旋度为0。
举例来说,如果气流或水流的旋度为0,表示没有涡流,F = xi + yj:
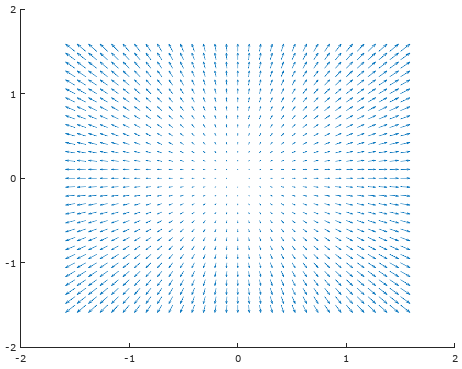
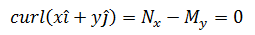
F = -yi + xj实际上是一个逆时针匀速转动的向量场,其旋度为2:
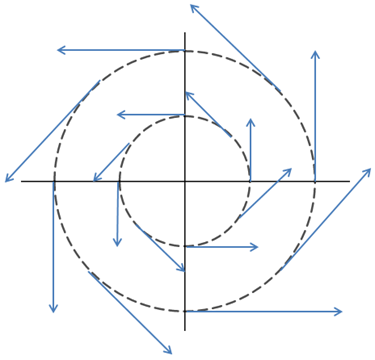
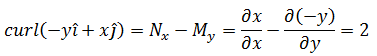
在复杂运动中,一些点的旋转可能比其他点多,此时旋度不是常数,它依赖于点所处的位置,也就是x和y的值。气象图中,高旋度的地方可能是台风或龙卷风:
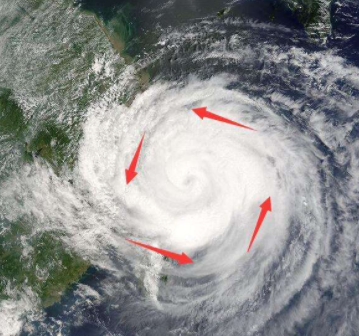
在力场中,旋度衡量的是任意一点所受的扭矩,或者说扭矩是力转动的对应量。
格林公式

如上图所示,在向量场中有一条闭合曲线C,其所围成的区域是R,如果要计算C的线积分,有两种选择,一种是直接计算,另一种是使用格林公式。
格林公式是另一种可以避免计算线积分的方法。格林公式是这样描述的:在处处有定义且处处可导的向量场F = Mi + Nj中,逆时针方向的闭合曲线C围成的区域是R,则C的线积分等于区域R上对旋度curl(F)的二重积分:
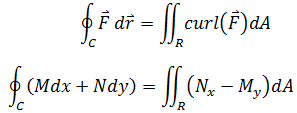
这是个奇特的结论,左侧的线积分定义在曲线上,而右侧的二重积分定义的是曲线内部的区域。之所以规定曲线是逆时针,是基于旋度的定义,如果曲线是顺时针,那么等式右侧就是∫∫R(My - Nx)dA。实际上格林公式也与保守场互相佐证,如果是保守场,My - Nx = 0,等式右侧的二重积分也为0。
公式的由来
这个怪异的公式是如何得到的呢?
点在场中的闭合曲线C上逆时针运动,尝试一个简化问题的验证,假设场是F = Mi,也就是N = 0,那么现在需要证明的是:
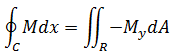
如果上式成立,则同理可证:

明确目标后先来看一个图示:

将C围成的闭合区域拆分成C1和C2两部分,它们都是逆时针方向。将C1和C2的线积分相加,将比C的线积分多计算了两次分界线。注意分界线上C1和C2的方向,发现二者相反,所以在分界线上二者抵消,故:
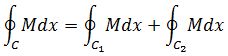
如果格林公式成立,则:
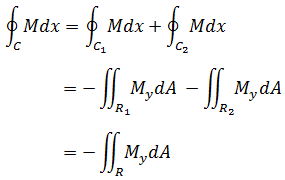
由此推广,对于更复杂的曲线,总是可以分成多个相对简单小区域,如果格林公式成立,则曲线的线积分等于所有小区域的二重积分之和。对于简单的小区域,可以划分成无数个竖直的矩形:

将矩形放大:
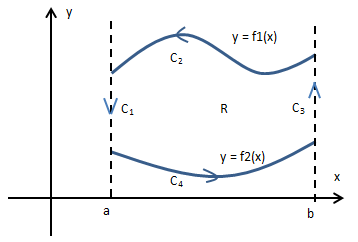
C1C2C3C4是矩形的四个边,C2和C4的曲线分别是y = f1(x) 和y = f2(x),上图中:
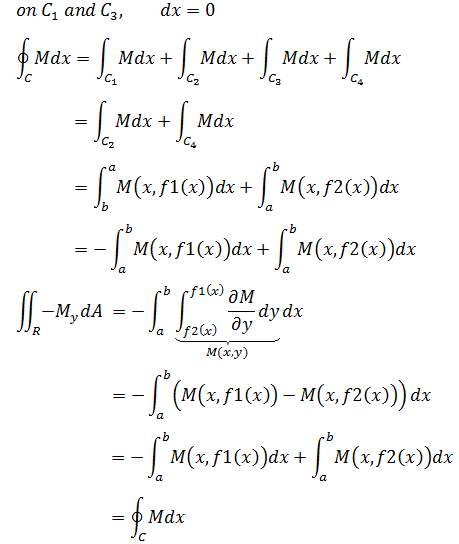
至此,达到了最初的目标,所以格林公式成立。
使用示例
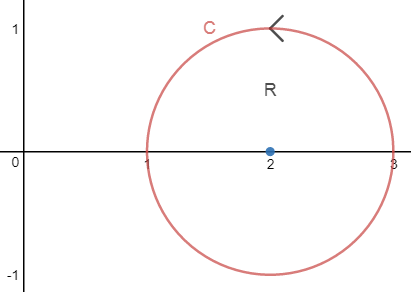
如上图所示,C是逆时针旋转的半径为1的圆,计算C在场中的线积分:

首先尝试直接结算,判断一下场是否是保守场:
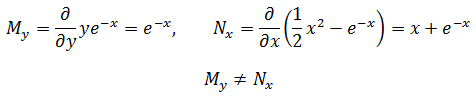
对x和y参数化:

代入后将得到令人抓狂的结果:
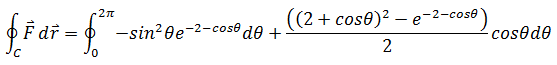
现在改用格林公式:
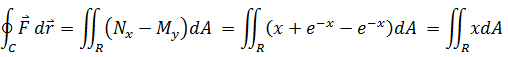
这是个不错的结果。为了避免计算复杂的积分域,所以积分域取1/4圆:

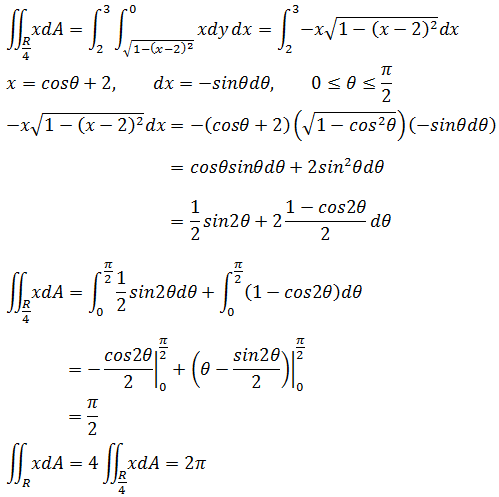
还有一种更简单的计算方式:

综合示例
示例1
场中的逆时针路径C是半径为a,圆心在x轴上的圆,计算:
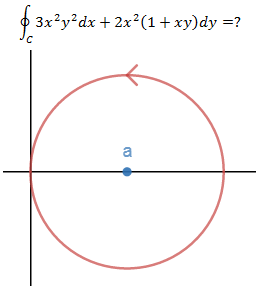
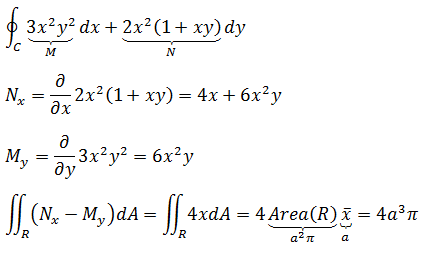
示例2
摆线的参数方程:x = a(θ – sinθ),y = a(1 – cosθ),a > 0,y ≥ 0,计算摆线与x轴围成的面积。
首先用描点法画出草图:
a > 0,y ≥ 0 => 1 – cosθ ≥ 0 => 0 ≤ θ ≤ 2π;
θ = 0,x = 0,y = 0; θ = π,x = aπ, y = 2a;θ = 2π,x = 2aπ, y = 0

根据格林公式:

其中的两种可能是:
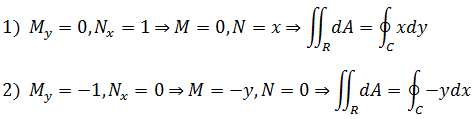
现在将二重积分变成了线积分,如下图所示,C = C1 + C2:
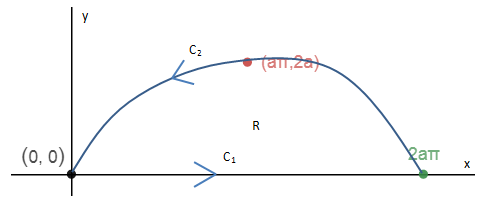
由于x的积分限更好确定,所以使用第二种解:
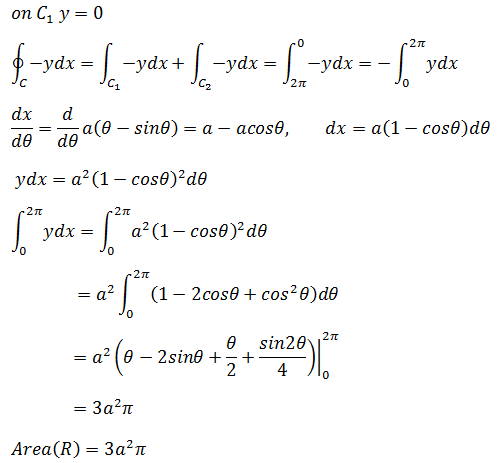
三角函数的积分可参考《数学笔记20——三角替换1(sin和cos)》
示例3
是否存在闭合曲线C,能够使下面的积分取最小非负值?
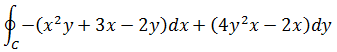
当C压缩成一点的时候,线积分会有最小值,但是最小值可能是负数,最小的非负值是什么?正负转换的边界曲线又是什么?
还是使用格林公式将线积分转换为二重积分:
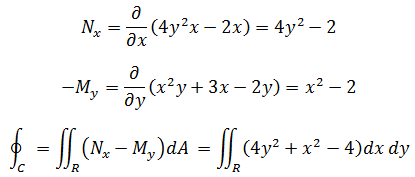
二重积分的被积函数是椭圆,从几何意义看来,积分最小时应当取面积最小的椭圆:
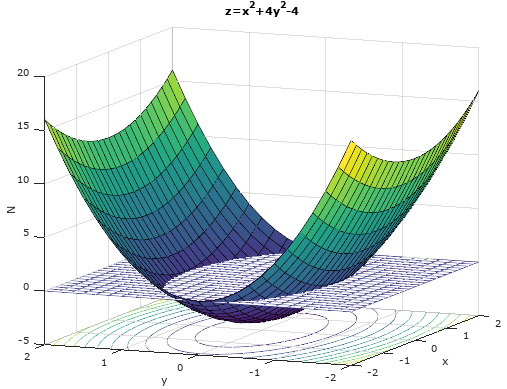
根据几何意义,二重积分是曲面与曲面在xy轴的投影所围成的体积,当 z = 4y2 + x2 – 4 < 0时,体积是负值,所以此时线积分也是负值。正负的边界就是g = 4y2 + x2 – 4 = 0,g所围成的面积是椭圆,所以曲线g就是所要寻找的线积分路径C。
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”
