ML（7）——支持向量机1（构建支持向量机）

　　支持向量机缩写是SVM（support vaector machine），这里的“机（machine）”是一个算法。在机器学习领域，常把一些算法看做是一个机器，如感知机（也叫感知器）。支持向量机本身是一种监督学习算法，它广泛的应用于统计分类以及回归分析中。

构建支持向量机

　　支持向量机的假设函数与逻辑归回一样，这里需要回顾一下逻辑回归的模型：

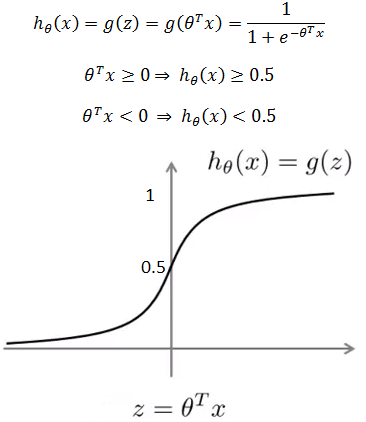
　　当实际值是1时，如果我们想让预测结果尽可能准确，则需要预测值是1的概率很大，即h_θ(x) ≈ 1，此时，θ^Tx >> 0；相应的，当实际值是0时，如果希望预测值尽可能准确，则h_θ(x) ≈ 0，θ^Tx << 0。对于逻辑回归的损失函数：

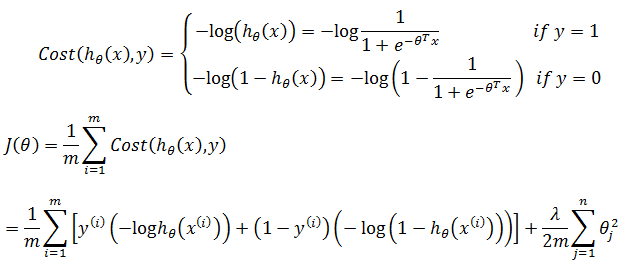
　　当y=1时，z = θ^Tx越大，预测结果h_θ(x) 越接近1，cost值越小；z = θ^Tx越小，预测结果h_θ(x) 越接近0，cost值越大：

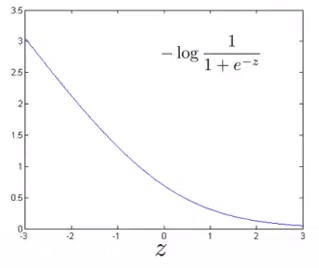
　　当y=0时，z = θ^Tx越大，预测结果h_θ(x) 越接近1，cost值越大；z = θ^Tx越小，预测结果h_θ(x) 越接近0，cost值越小：

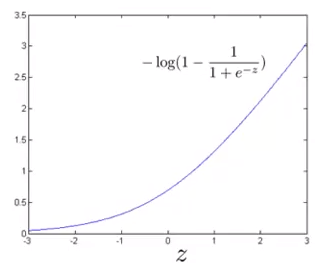
　　支持向量机的cost function可以看作逻辑回归的退化，它将曲线变为直线：

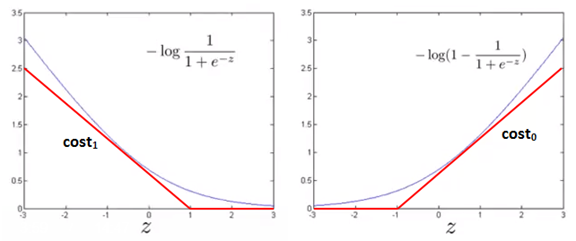
　　这里的cost₁和cost₀是对称的，都是折线函数，其斜率和截距可以自行选定。上图中的cost可能是：

 

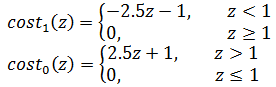
　　因为1/m是常量，对最终的优化不起任何作用，所以习惯上支持向量机损失函数去掉1/m：

 

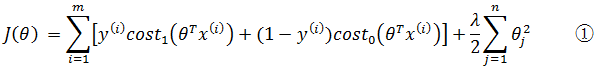
　　上式中λ是常量，相应地，1/λ同样是常量，对于最终目标（求得最佳θ使J(θ)最小化）来说，乘以一个常数对计算没有任何影响，所以上式可乘以1/λ：

 

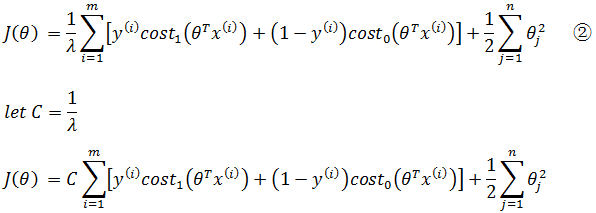
　　对于优化来说，①和②最终将得到同样的结果，其中λ在优化中起到的作用一样，如果过拟合，需要增大λ（减小C），欠拟合需要缩小λ（增大C）。

　　我们使用一个极端的例子，假设C设置的很大，为了使J(θ)最小化， 需要让C控制的表达式接近0：

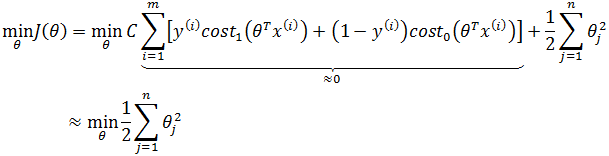
　　因为C相当于1/λ，C很大等价于λ很小，这将产生过拟合：

安全距离的直观理解

　　假设支持向量机代价涵数的曲线如下所示：

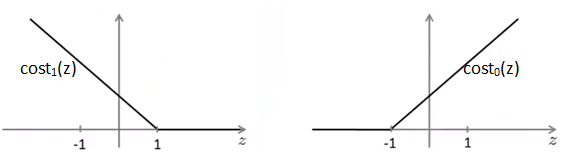
　　对于二分类来说：

 

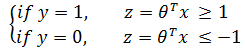
　　结合最小化J(θ)：

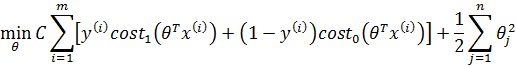
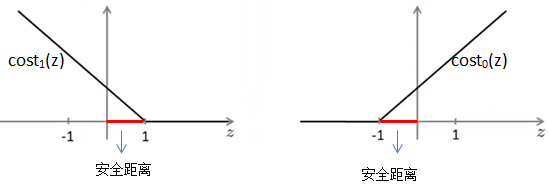
　　对于能够正确分开的正样本，逻辑回归要求z = θ^Tx ≥ 0，而SVM要求z = θ^Tx ≥ 1，此时cost₁(z) = 0；对于正确分开的负样本，逻辑回归要求z = θ^Tx < 0，而SVM要求z = θ^Tx ≤ -1，此时cost₀(z) = 0。可见SVM要比逻辑回归严格，相当于多嵌入了一个额外的安全距离因子，也就是cost的函数斜线部分的截距：

 

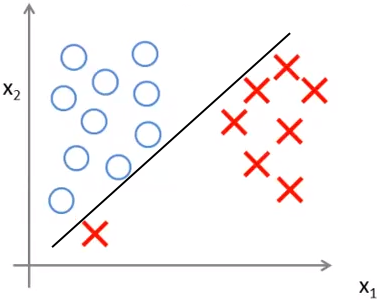
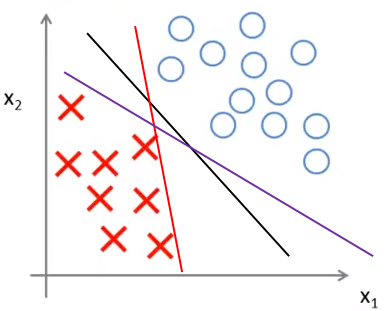
　　用一个例子说明安全距离的作用。对于一个有两个特征的线性可分的训练集，下图中的三条直线都能将样本正确分类：

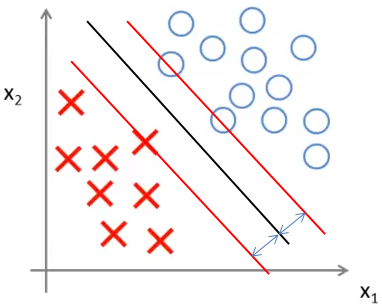
　　实际上支持向量机会选择更安全的黑色直线，因为它距离两侧的分类都有足够的距离，也就是说，相对与其他分隔线，如果选取黑色直线，那么分隔线和距离其最近的样本点的距离比其它直线要大：

与逻辑回归的区别

　　在逻辑回归中，正例的h_θ(x)≥0.5，负例的h_θ(x)≤0.5，强调在全部训练实例上达到J(θ)最小化的目标，其分隔平面如下所示：

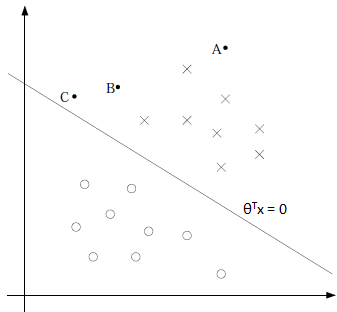
　　逻辑回归强调所有点尽可能地远离分隔平面，更准确地说是所有点的损失函数之和最小，为了达到这个目的，可能会使一部分点十分接近分隔平面从而换取另一部分点更加远离平面。从图中我们可以确定A是×类别，B还算能够确定（比如h_θ(x) = 0.65），C是不太确定的（比如h_θ(x) = 0.55）。可以说，逻辑回归关心的是全局。

　　但是实际应用中，我们更关心靠近分隔平面的模棱两可的点，而不是十分确定的点，SVM的思路正是通过拉近远离分隔平面的点，从而换得原来靠近平面的点能够远离平面。

间隔和支持向量

　　在线性可分的情况下，支持向量机的分隔线仅与几个最靠近它的点有关，这些点称为支持向量，下图中H是分隔直线，H₁上的1个点和H₂上的2个点是支持向量，也称为支撑向量：

 

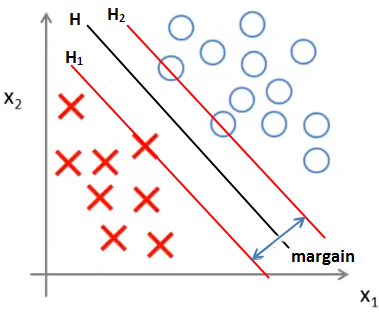
　　下一篇的内容：支持向量机的模型函数；如何寻找最大间隔 

 

　　参考

　　Ng视频 《Support Vector Machines》

---

 　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”