关于最简行阶梯矩阵和矩阵秩,可参考《线性代数笔记7——再看行列式与矩阵》
召唤一个方程Ax = b:
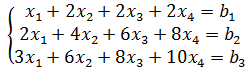
3个方程4个变量,方程组有无数解,现在要关注的是b1b2b3之间满足什么条件时方程组有解,它的解是什么?
在这个例子中可以马上看出,b1+b2 = b3,一般的方法是消元法化简:
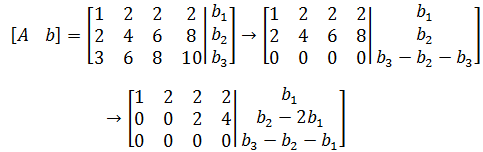
化简到这一步就可以确定主元是x1和x3。通过最后一行可知,b3 – b2 - b1 = 0。b1b2b3可以是任意数,所以只要满足b3 – b2 - b1 = 0,方程组就有解。这样的组合很多,可以很容易找到一个特解:

现在我们知道了b中三个分量的关系,并且还知道只有当 b属于A的列空间时有解。通过上一章的方法可知,列空间的基就是主元所在的列:

到此为止回答了第一个问题,什么样的b才能使Ax = b有解。现在需要回答另一个问题,Ax = b的所有解是什么?
可以先找出一个特解,方法是令所有自由元为0,然后解出主元:
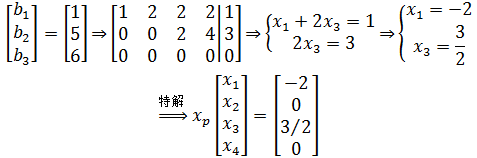
已经找到了一个特解,那么方程组的其它解,也就是通解是什么呢?
假设Ax= 0的零空间的任意向量是xn,Ax = b有一个特解xp,那么有:

二者相加:

所以方程组的通解是xn + xp。对于方程组的某解xp来说,xp与零空间内任意向量之和仍为解。现在看看零空间:
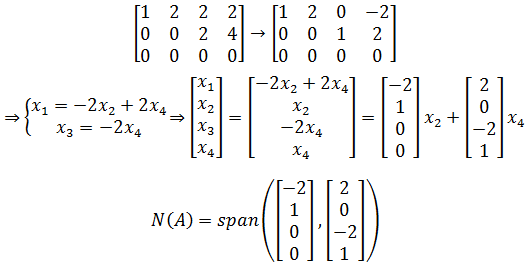
综合特解,得到Ax = b的通解:

矩阵的秩和主元个数相同。如果A是一个m行n列的矩阵,其主元的个数一定小于m,并且也小于n。如果A的每一列都有主元,那么A是满秩矩阵,没有自由元,如果此时有解,则解是唯一的,就是特解,即x = xp,此时不需要求解零空间,零空间只包含零向量。
作者:我是8位的
