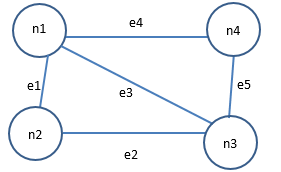
图(Graph)是离散数学中的一种常见数据结构,由节点和边组成,如果边有方向,就是有向图。下图是一个有4个节点5条边的有向图:

这个图(Graph)可以表示电网、网络或建筑物通道的数学模型。
关联矩阵
可以通过一个矩阵来解析有向图,这个矩阵称为关联矩阵(Incidence Matrix)。4个节点5条边的图用一个5×4的矩阵表示,用正负表示边的方向,矩阵的一行相当于图的一条边,矩阵的一列对应图的一个节点:

以A的第一行为例,它对应图的第一条边e1,e1的方向是从n1指向n2,与n3和n4无关。如果将A中的-1全部改为1,就变成了无向图。
A的前三行对应了三边e1,e2,e3,它们构成了图中的一个回路。对于一个图来说,回路的数量和位置至关重要。把回路单独拿出来看:

问题之一是:这三行相互独立吗?或者说它们是否是线性无关的?
似乎很容易看出,第3行可以由第1行和第2行相加得到,这说明回路对应的行是线性相关的。从图上看,从n1到n3可以n1→n3,也可以n1→n2→n3,所以说n1→n3是“多余”的,它可以由“绕行”代替。
存储大型关联矩阵
如果用关联矩阵描述一个大型图,你会发现矩阵中的0非常多,这个矩阵是一个稀疏矩阵。用计算机存储这个矩阵时,应当考虑是否应该用邻接表代替二维数组,同时也可以使用一维数组代替二维数组。
邻接表是一种常用的数据结构,它是一个存储了链表的一维数组。
还是这个图,现在不考虑方向,用一维数组描述:
L[4]是有4个节点的数组(假设数组下标从1开始,和Matlab一样),初始元素都为0,这样构造数组:
n1与n2联通,将L[1]与L[2]赋予n2的序号,L = [2,2,0,0];
n2与n3联通,将L[2]和与L[2]相连的所有节点都赋予n3的序号,L = [3,3,3,0];
n3与n4联通,将L[3]和与L[4]相连的所有节点都赋予n4的序号,L = [4,4,4,4]。
对于回路不必重新负值:
n1与n4联通,但是它们之间已经有回路了,L[1] == L[4];
n1与n3联通,它们之间同样有回路,L[1] == L[3]。
最终,L = [4,4,4,4],判断两点np与nq是否联通,只需要判断if L[p] == L[q]即可。
关联矩阵的零空间

如果A的零空间是零向量,则意味着Ax = 0有唯一解,此时A应当是方阵,A的行最简阶梯矩阵是单位矩阵,A的各列线性无关。
A不是方阵,所以x没有唯一解。这很容易验证,Ax = 0中,x有4个分量,方程组中有5个方程,但只有4个未知数,所以方程有无数解。

只要x1 = x2 = x3 = x4,就满足Ax = 0。A的零空间是位于R4空间下的1维空间:
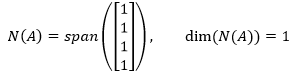
如果A是电网,xn表示每个节点的电势,则上面的N(A)意味着所有节点的电势相等,不存在电势差,因此不存在电流。如果把n4节点接地,就会产生电势差,此时相当于将x4的电势设为0:
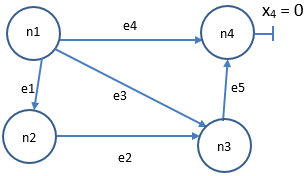
对于Ax来说,x4 = 0意味着A的最后一列不起作用(最后一列的各个分量与0的相乘总是0)。这样,A前三列就变成线性无关,实际上A的任意三列都是线性无关,A的秩是3。
作者:我是8位的
