标准正交矩阵
标准正交向量
有一堆向量,q1,q2……qn,它们两两正交,这意味着这些向量满足:
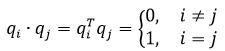
一个向量没法和自己正交,在i = j时,让qiTqi = 1,这相当于qi模长等于1:
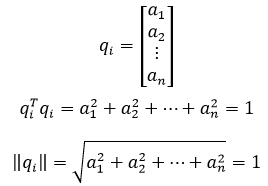
向量的转置乘以自身等于1,意味着这个向量是单位向量,所以我们称这堆向量q1,q2……qn是标准正交向量。
标准正交矩阵
现在把这些标准正交向量放入矩阵中:
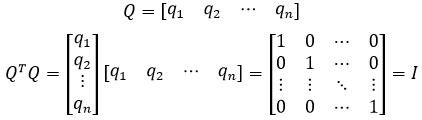
QTQ最终得到了一个单位矩阵,但Q本身未必是方阵。Q的列是标准正交的,Q因此被称为标准正交矩阵;当Q是方阵时,简称为正交矩阵,此时说明Q和QT互为逆矩阵:
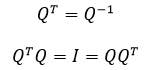
下面的Q就是一个正交矩阵:

可以将Q的三个列看作直角坐标系的三个轴,它们两两垂直。
再举个例子:
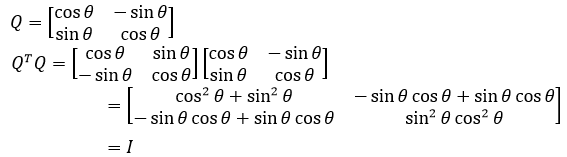
一个方阵的列是正交的并不意味着方阵是正交矩阵,比如下面这个:
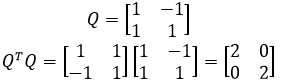
虽然这个矩阵不是正交矩阵,QTQ的结果却与单位矩阵神似,我们可以对Q做点处理让它变成正交矩阵。当Q是正交矩阵时,Q的每一个列的模长都应该是1,因此可以这样处理:
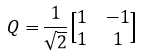
这样就变成正交矩阵了。类似的还有下面这个:
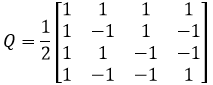
正交矩阵与投影矩阵
如果Q是标准正交矩阵,那么Q在列空间上的投影矩阵将得到简化:
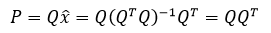
更进一步,如果Q是方阵:
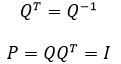
如果对QQT再次投影(这里并未强调Q是方阵):
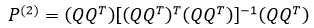
其中:
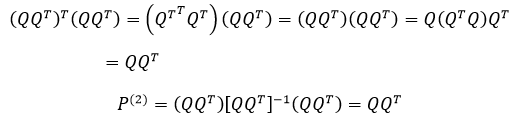
在求解Ax = b时,如果A是标准正交矩阵,它的好处就是不需要计算逆矩阵:
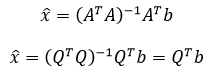
这也意味着x帽的一个分量等于QT一行(或Q的一列的转置)与b的点积:
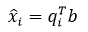
这也是很重要的一个式子:如果已知标准正交基,在第i个基方向上的投影就等于qiTb
格拉姆-施密特正交化
既然正交化这么好,有没有什么方法能使矩阵标准正交化呢?当然有,这就是格拉姆-施密特(Gram-Schmidt)正交化。
假设有两个线性无关的向量a和b,现在标准正交化这两个向量,让它们变成q1和q2。首先保持a不变让向量A = a,接下来要寻找到另一个向量B,使得A⊥B。p是b在a上的投影,B就相当于b的误差向量:
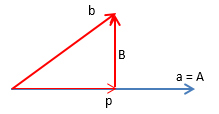
根据上一章的知识,p相当于a放缩了x倍,在一维空间内,x是一个标量:
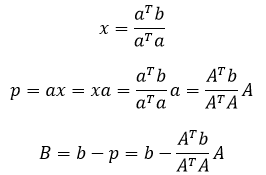
这相当于B是b减去b在a上的投影,B是b和A的线性组合。
最后将A变成指向A方向的单位向量,B变成指向B方向的单位向量:
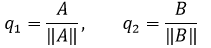
这就是格拉姆-施密特正交化方法。
如果还有一个向量c,由c到q3的转换:
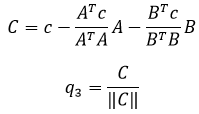
代入几个数值看看:
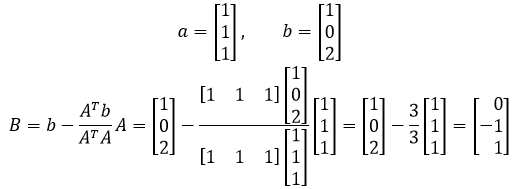
验证:
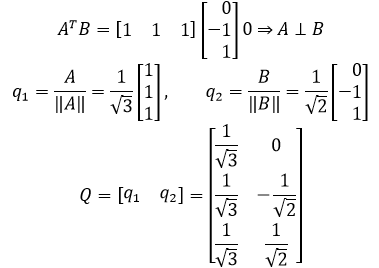
这个标准正交矩阵Q是通过下面的原始矩阵得到的:
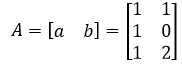
A的列空间和B的列空间相同,能够张成一个二维空间的平面。a和b是A的列空间的一组基,但这组基“不够好”,我们还想进一步让这组基的向量两两正交,并且都是单位向量,这就得到了q1和q2。
格拉姆-施密特表达
如同A = LU一样,A可以分解成一个正交矩阵和一个上三角矩阵的乘积,A = QR,这里A是原始矩阵,各列线性无关,Q是标准正交矩阵,R是上三角矩阵。
假设原始矩阵A有三个列向量:
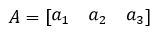
按照格拉姆-施密特正交化方法转换后,得到q1,q2,q3:
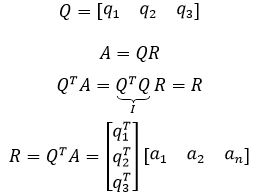
q和a本身也是列向量,得出结果并不那么直观,可以展开表达:
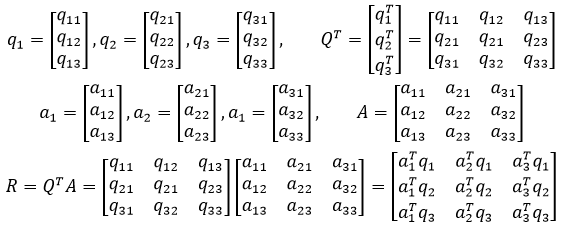
由于q1Tq2 = 0,q1只是a1的单位化,所以a1T与q2也正交,a1Tq2 = 0;同理,a1Tq3 = 0。q2是a2和q1的线性组合,转置后,q2T是a2T和q1T的线性组合,这相当于:
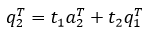
如果t1 = 0,相当于q1和q2是线性相关的,这就不符合标准正交向量的前提,所以一定有t1 ≠ 0:
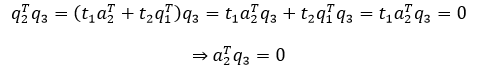
a2Tq2和a3Tq3不为0,如果是0,就没必要正交化了。q3是a3和q1、q2的线性组合,转置后,q3T是a3T和q1T、q2T的线性组合,这相当于:
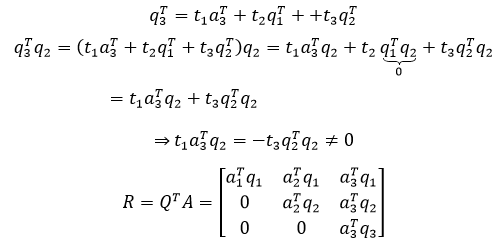
示例
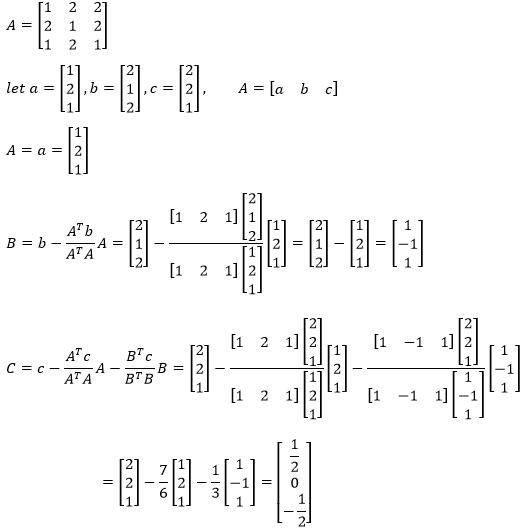
求矩阵A的QR分解。

作者:我是8位的
