SDN网络中hypervisor带来的控制器时延（Hypervisor位置的优化）

　　一，问题背景

1.介绍监督器大部分由软件实现，可灵活放置，高效的SDN网络虚拟化需要复杂的技术来放置hypervisor在合适的位置，才能提供租户最佳的性能。称为k-Network Hypervisor Placement Problem（k-HPP）。

k-HPP回答了，监督器实例应放置k个，放在那里的问题。

2.交换机特性不能，有的交换机只能连接单个控制器，有的交换机可连接多控制器。因为Hypervisor是在控制器和交换机之间，而无Hypervisor时控制器直接与交换机相连，因此Hypervisor代替了控制器与交换机相连。也就是说多控制器交换机也就支持与多个Hypervisor实例相连。

3.设监督器实例数量为k

  多控制器减缓及数量为m。

对于几种结构的Hypervisor示意图如下：

A.网络中心化Hypervisor结构。

也就是k=1

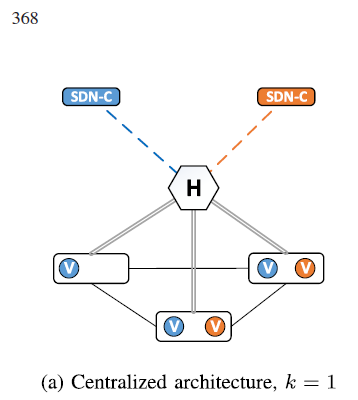
B.对于单控制交换机，分布式网络Hypervisor结构.

也就是k>1,m=0。对于每个Hypervisor划分一个控制域

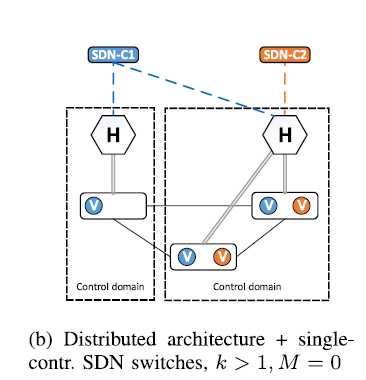
C.对于多控制器交换机，分布式网络Hypervisor结构

k>1,且每个交换机都支持多控制器。因此无控制域划分。

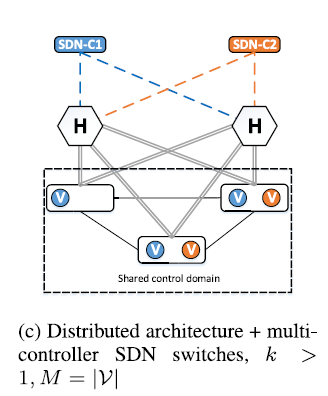
D.混合型分布式网络Hypervisor结构

k>1,有的交换机支持多控制器，有的不支持

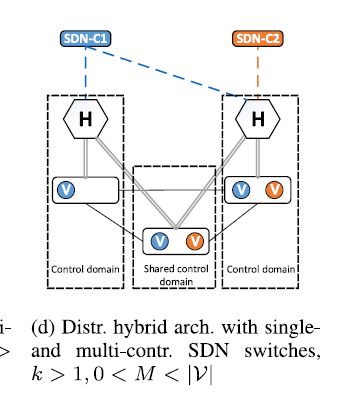
二，对于k个网络监督器放置问题（k-HPP）和多控制器交换机部署问题的设置（Multi-Controller Switch Deployment Problem  McSDP）

A.网络模型

k-HPP输入为一系列的vSDN请求R，以及给定要在其上实现的物理网络图G（V,E）

1）物理SDN网络说明：

　　网络被模型化为图G（V,E），

　　物理交换机节点v∈V，

　　被无向边连接e∈E，

　　可能的Hypervisor节点位置由集合Φ给出，Φ∈V，

　　边e的时延由通过e连接的两个节点间地理距离得出，用来评估网络路径时延，记λ(e)，

　　集合P，包含网络中任意节点对间最短路径，距离也就是时延，最短路径记 d(s,t)∈P，

　　d(s,v,t)表示经过v，s到t的最短路径。等于d(s,v)+d(v,t)

2）虚拟SDN网络请求：

　　一个vSDN请求r∈R，

　　被定义为一系列虚拟SDN网络节点V^r，和vSDN控制器cr，

　　vSDN节点的对应物理节点由函数，π（v^r）给出,π（v^r）∈V，

　　控制器位置也要在可利用的网络节点位置中选出，π（c^r）∈V。

　　所有vSDN节点都要连接到他们的控制器实例，每个vSDN仅操作一个控制器。

B.k-HPP问题

　　输入为G、R、k、M。

　　k个Hypervisor位置要在Φ中选出。最佳化问题的结果是被选中Hypervisor位置集合H。

三，混合整数规划模型来解决k-HPP和McMcSDP

A.确定变量

　　X_H（v）确定是否一个Hypervisor被放在网络节点（位置），v∈Φ，

　　在解决这个模型问题后得到一个集合H=｛v∈Φ：X_H（v）=1｝，

　　X_R（v^r，h，c^r）设为1，如果vSDN节点v^r∈V^r连接到控制器c^r，经过监督器节点（位置）h∈Φ，否则为0，

　　X_V,H（v，h）指示是否物理节点v被在h上的监督器实例控制。被控制为1，否则0，

　　X_M（v）节点v是否支持多控制器特性，1表示支持，否则0，

B.目标函数

　　引入四个时延度量，也就是最大时延L_max，平均时延L_avg，平均最大时延L_avgmax，最大平均时延L_maxavg。

　　平均和最大时延是传统的度量来自相关的SDN控制器放置问题，我们延伸这个问题到kHPP上。来优化L_max、L_avgmax、L_maxavg时，需要额外的变量和限制。

　　1）最大时延：对于一个考虑的hypervisor位置最大时延就是所有请求r∈R中所有被利用最短路径的最大时延。所有路径中最大时延可以被选出通过执行请求r∈R

　　　　

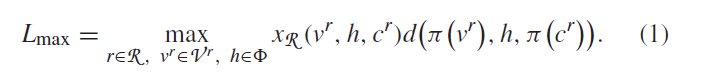
　　最小化最大时延涉及到最小化最大遍历集，这没有直接答案。最大对集可以被表达为相等的限制最小化问题。我们能等价地最小化L_max通过定义限制

　　　　

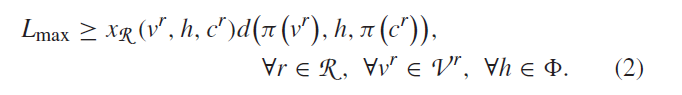
　　结果的目标函数就是

　 　

　　2）平均时延：平均时延就是所有vSDN，连接虚拟网络节点和各自vSDN控制器的所有路径延迟的平均值。

　　　　对于一个vSDN请求r，有丨V^r丨个vSDN节点需要连接到vSDN控制器c^r，所以对于一系列请求R，共Σ_r∈R丨V^r丨条路径，所以平均时延为：

　　　

　　　　这个度量在不同vSDN中不会不同，因此不需要额外的变量和限制，所以平均时延目标函数为

　　　

　　3）平均最大时延：对于一个给定hypervisor位置，其平均最大时延定义为每个个体vSDN请求r∈R的最大时延的平均。

　　　第一是，每个vSDN请求的最大路径时延被评估；第二是，所有最大路径值得平均值被评估，也就是最大路径延迟的和被总vSDN请求数R除。

　　　　

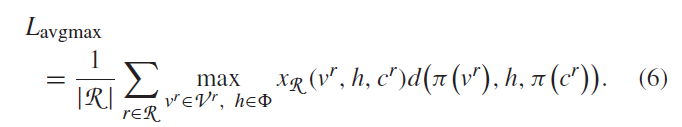
　　　为了避免遍历集合最大值，我们为每个给定的vSDN请求r的最大时延定义限制：

　　　　

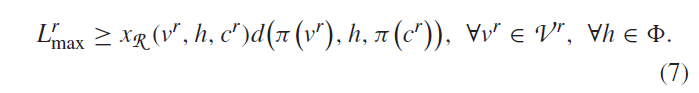
　　　最小化遍历所有请求的L^r_max　的平均值的目标函数：

　　　　

　　　这个目标函数提供一个不严格的平均值，为了每个vSDN更好的最大时延。这个目标函数对于不同的vSDN是不同的。

　　4）最大平均时延：定义为每个不同vSDN平均时延的最大值。第一，每个vSDN请求r的平均时延被确定，第二，这些平均值的最大值被评估，

　　　　　

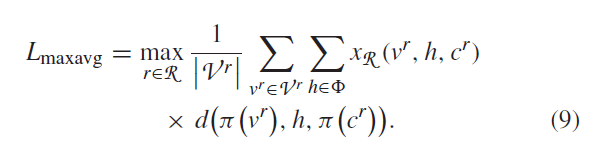
　　 这个度量符合vSDN平均时延的最大值，也就是说最大时延每个vSDN不严格，为了更好的总的最大平均时延。最小化遍历R的最大值等价于最小化L_maxavg通过定义限制：

　　　　

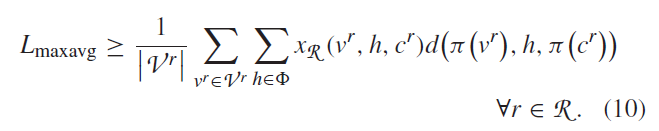
　　这样目标函数就最小化了L_maxavg，

　　　　min L_maxavg.（11）

C.限制

　　1）Hypervisor选择限制：

　　　　确保放置的Hypervisor数量等于k

　　　　

　　2）虚拟节点路径选择限制：

　　　　每个vSDN请求r的每个虚拟节点v^r必须连接到它相应的控制器经过一个Hypervisor节点h。也就是每个请求的每个虚拟节点有一条路径被使用

　　　　 

　　3）虚拟节点安装限制：

　　　　我们放置一个Hypervisor实例在位置h上，如果至少有一个虚拟节点连接到控制器经过了h。那么，同时最多Σ_r∈R丨V^r丨个虚拟节点能通过h连接到他们各自的控制器。

　　　　    （有个疑问，最多也就Σ_r∈R丨V^r丨个节点，所以肯定不会超过这个数，设这个限制有什么意义）

　　4）物理节点对于Hypervisor分配限制

　　　　让一个Hypervisor节点h控制一个物理交换机节点v，如果一条路径选择连接虚拟节点v^r到他的控制器c^r经过h,并且这个虚拟节点由v来服务。因此

　　　　

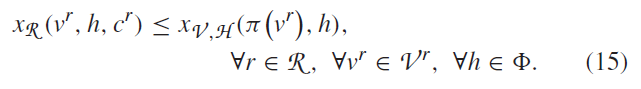
　　5）多个Hypervisor限制：
　　　　对于一个给定的多控制器交换机v，控制的Hypervisor数量必须小于或等于总数量k（如果这个交换机至少服务一个虚拟节点）。

　　　对于单交换机控制器v,控制的Hypervisor数量必须等于1（如果这个交换机至少服务一个虚拟节点），因此对于任意物理交换机v

　　　　

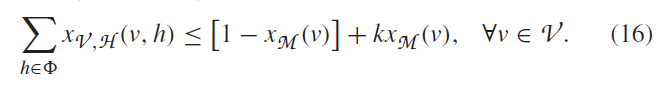
　　　　我们要注明，一些解决者没必要的设置X_V,H（v，h）为1，甚至是对于一个节点v，没有任何的虚拟节点连接到其控制器经过Hypervisor节点h。

　　这是因为解决者通过设置这些没必要的节点可以有效的找到最小时延。为了限制这个问题，我们设其为0，当没路径通过时：

　　　　

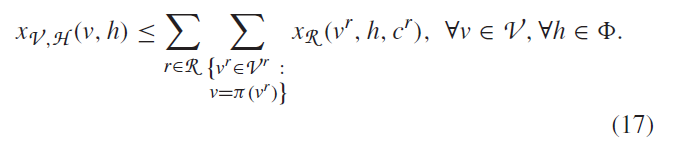
　　6）多控制器交换机限制：
　　　　

　　

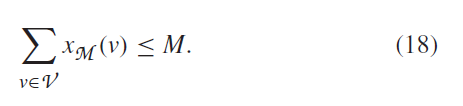
　　这样通过这些限制和4种不同的结构就能模型化，最佳化，和分析这个问题。

四，后面是对这些模型的评估。