正交投影矩阵_相机中的透视投影几何——讨论相机中的正交投影

相机中的透视投影几何——讨论相机中的正交投影，弱透视投影以及透视的一些性质

前言

相机中的成像其本质是从3D实体世界中的物体投影到2D成像平面上，在这个过程中存在着许多投影相关的内容，本文讨论了一些透视投影的内容，

相机的针孔模型

我们曾经在[1]中讨论过关于相机的针孔模型的话题，这里我们要再次提起下这个模型。针孔模型(pinhole model) 是最简单的可以成像的“设备”，然而其可以精确地得到 透视投影(Perspective Projection) 的几何信息，这里所说的透视投影，定义为：

将三维物体的信息映射到二维平面上，称之为透视投影。( Such a mapping from three dimensions onto two dimensions is called perspective projection. )

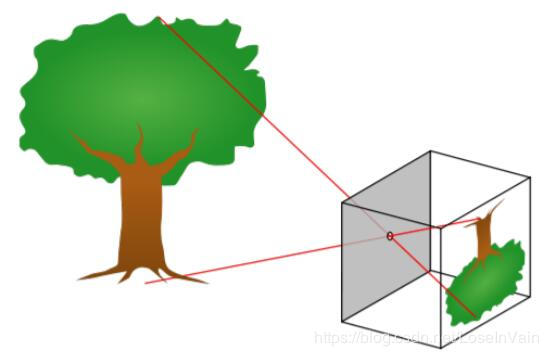
Fig 1.1 相机的针孔模型及其透视投影成像。

在针孔模型中，光线通过一个无限小的孔，并且在成像平面上呈现出倒像。呈现出倒像不方便我们的分析，因此我们在分析时通常假设成像平面在焦点之前，距离同样也是焦距（未归一化之前，归一化之后距离就是1了，称之为归一化坐标系）。

透视投影的方程

我们需要用代数方式描述透视投影中的比例关系，如图Fig 2.1所示，根据相似三角形的知识，我们有：

其中的

是焦距。

联合公式(2.1)和(2.2)，我们有透视投影公式:

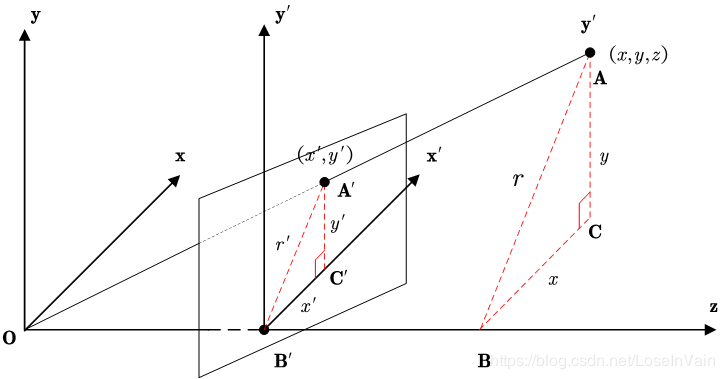
                                                         Fig 2.1 透视投影示意图。

透视投影的若干性质

多对一映射，在透视投影中，已知了投影点
之后，其实体点
并不是唯一的，而是存在于过焦点连线
上的任意一点都有可能(不过要在
之后呢，所以应该是在
的延长射线上。)
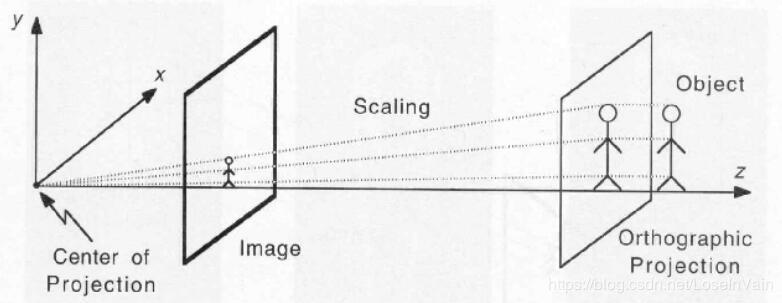
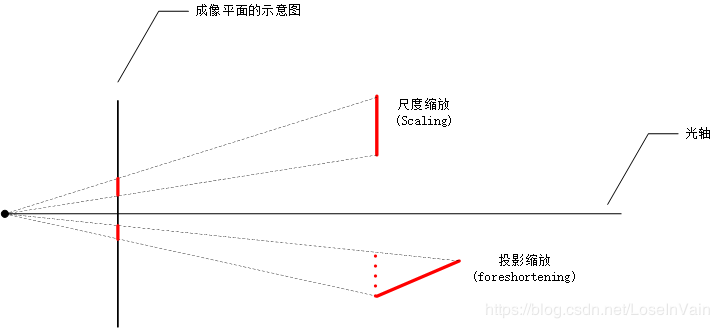
放缩和投影缩放。
当一个平面或者一条直线平行于成像平面时，透视投影的影响其实就是对这个平面/直线进行了缩放(scaling)。
当一个平面或者直线不平行于成像平面时，透视投影的会产生非线性的投影扭曲(projective distortion)，可以将其分解成平行于成像平面的分量的缩放。

焦距的若干影响

如图Fig 2.3 所示，不同焦距有着不同的影响，我们发现，焦距越小，其视角越大，属于广角摄像头(wide-angle camera)；焦距越大，其视角越小，但是分辨率会提高，属于望远镜摄像头(more telescopic)。

Fig 2.3 不同焦距的影响。

在透视投影中，在投影过程中，实际的平行关系通常不能保留下来，实际上，透视投影保留不了角度，距离等大部分的几何关系，但是保留了直线的“直”的这个属性。[2]

正交透视投影

注意到透视投影一般来说是非线性的，其不保留原始元素的大部分几何属性，比如平行，角度等，为了分析方便，我们假设当焦距无限大时，我们在成像平面上会存在一个所谓的正交投影，这个正交投影可以保留平行关系。其每个投影线都是平行的。这个称之为正交投影(orthographic projection)。

弱透视投影

 正交投影的尺度大小是和原始物体的大小一致的，当考虑的正交头像的尺度缩放时，就有了弱透视投影(weak perspective projection)。