最小生成树之Prim算法

生成树

 一个连通图的生成树是一个极小连通子图，它含有图中全部n个顶点和构成一棵树的(n-1)条边。　　

• 连通图由一次遍历就可以产生生成树
• 由深度优先遍历得到的生成树称为深度优先生成树。
• 由广度优先遍历得到的生成树称为广度优先生成树。

一个连通图的生成树不一定是唯一的！

最小生成树

对于带权连通图G （每条边上的权均为大于零的实数），可能有多棵不同生成树。
每棵生成树的所有边的权值之和可能不同。
其中权值之和最小的生成树称为图的最小生成树。

Prim算法

普里姆（Prim）算法是一种构造性算法，用于构造最小生成树。过程如下：

1. 初始化U={v}。v到其他顶点的所有边为候选边；
2. 重复以下步骤n-1次，使得其他n-1个顶点被加入到U中：
3. 从候选边中挑选权值最小的边输出，设该边在V-U中的顶点是k，将k加入U中；
4. 考察当前V-U中的所有顶点j，修改候选边：若(j，k)的权值小于原来和顶点k关联的候选边，则用(k，j)取代后者作为候选边。
   

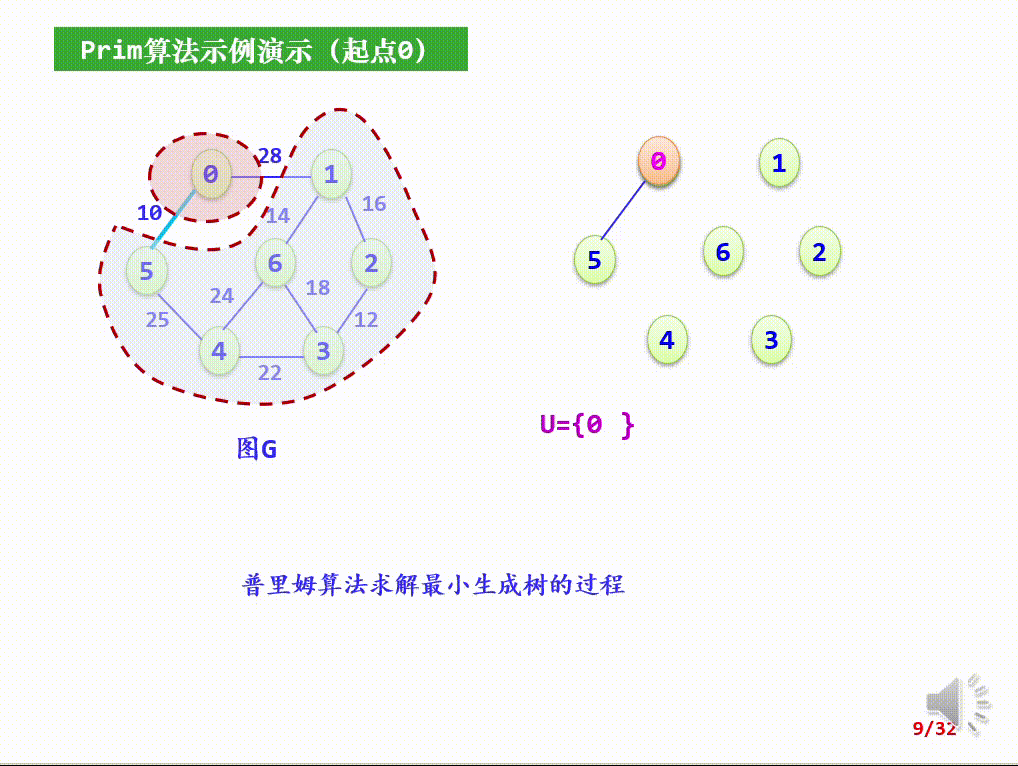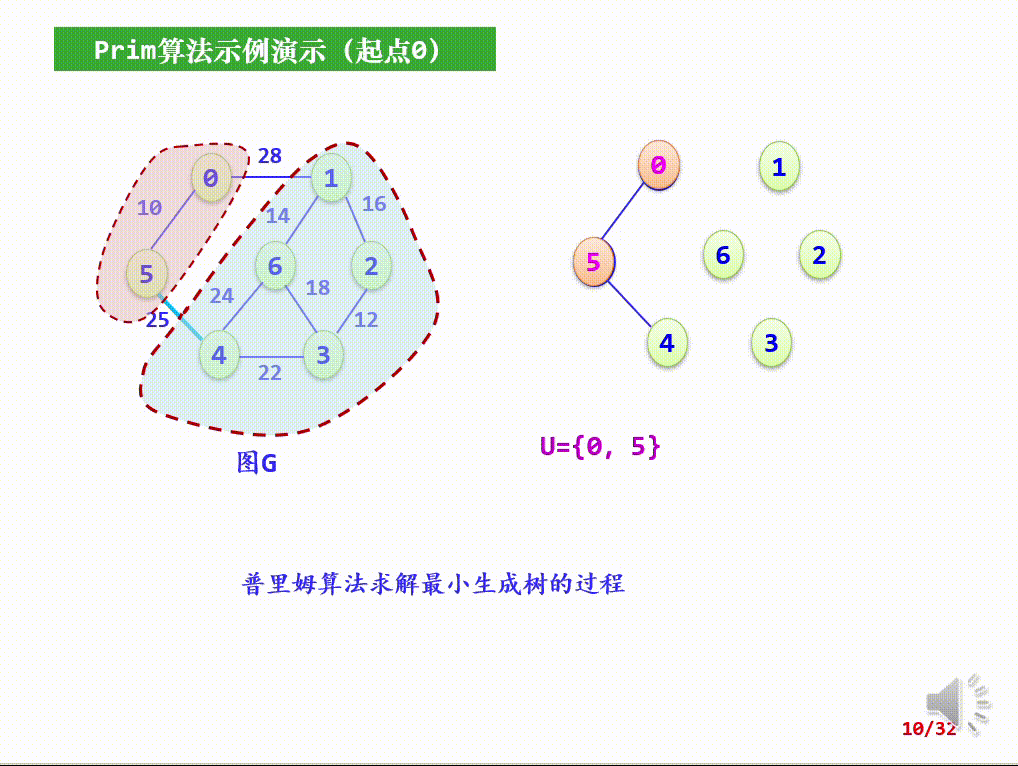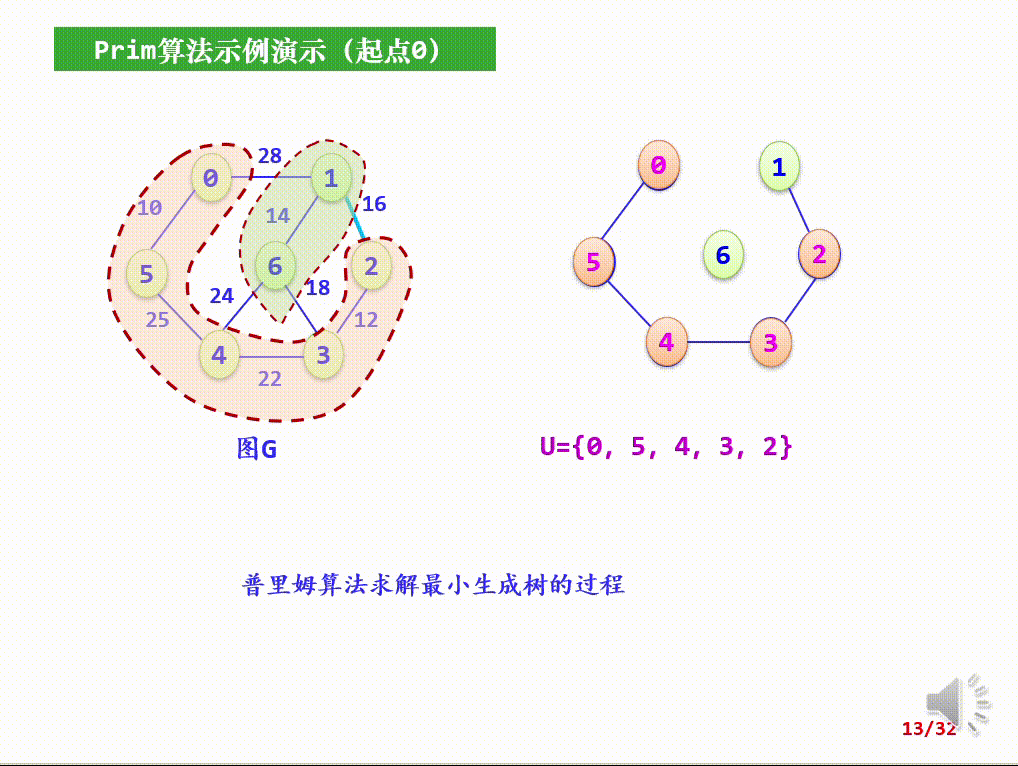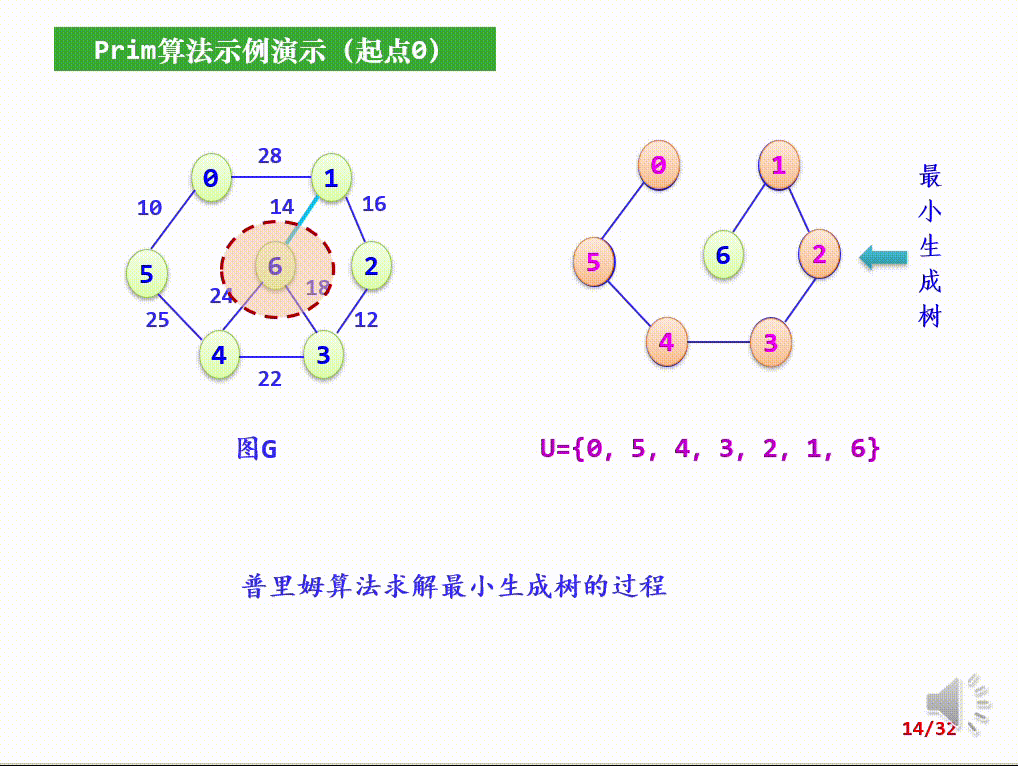
代码

Prim 算法构造生成树

//Prim 算法构造生成树
void Prim(MatGraph g, int v)
{
    int lowcost[MAXV];//存储权值
    int MIN;
    int closest[MAXV], i, j, k;
//closet是用来存储与它相邻的节点的
    for (i = 0; i < g.n; i++)
    {
        lowcost[i] = g.edges[v][i]; //初始化
        closest[i] = v;
    }
    for (i = 1; i < g.n; i++)
    {
        MIN = INF;
        for (j = 0; j < g.n; j++)
            if (lowcost[j] != 0 && lowcost[j] < MIN)
            {
                MIN = lowcost[j];
                k = j; //记录最近的节点的编号
            }
        printf("边(%d,%d)权为：%d
", closest[k], k, MIN);
        lowcost[k] = 0;

        for (j = 0; j < g.n; j++)
            if (lowcost[j] != 0 && g.edges[k][j] < lowcost[j]) //寻找有没有比较小的边
            {
                lowcost[j] = g.edges[k][j];
                closest[j] = k;
            }
    }
}

测试代码

# include <stdio.h>
# include <stdlib.h>
#define ElemType int
#define maxsize 100
#define InfoType int
#define MAXV 100
#define MaxSize 100
#define INF 214748364 
#define INFINITE INF
//邻接矩阵的数据类型
typedef struct s
{
    int no;     //顶点编号
    InfoType info;//顶点的其他信息
} VertexType;      //顶点的类型

typedef struct SS
{
    int edges[MAXV][MAXV]; //邻接矩阵的数组
    int n, e;              //图的顶点数和边数
    VertexType vexs[MAXV]; //存放顶点信息
} MatGraph;
///////////////////////////////////////////////////

//Prim 算法构造生成树
void Prim(MatGraph g, int v)
{
    int lowcost[MAXV];
    int MIN;
    int closest[MAXV], i, j, k;

    for (i = 0; i < g.n; i++)
    {
        lowcost[i] = g.edges[v][i]; //init
        closest[i] = v;
    }
    for (i = 1; i < g.n; i++)
    {
        MIN = INF;
        for (j = 0; j < g.n; j++)
            if (lowcost[j] != 0 && lowcost[j] < MIN)
            {
                MIN = lowcost[j];
                k = j; //记录最近的节点的编号
            }
        printf("边(%d,%d)权为：%d
", closest[k], k, MIN);
        lowcost[k] = 0;

        for (j = 0; j < g.n; j++)
            if (lowcost[j] != 0 && g.edges[k][j] < lowcost[j])
            {
                lowcost[j] = g.edges[k][j];
                closest[j] = k;
            }
    }
}
//////////////////////////////////////////////////////////////
void InitMatGraph(MatGraph & g, int a[][MAXV], int n, int e)
{
    int i, j;
    g.n = n;
    g.e = e;
    for(i = 0; i< n; i++)
        for(j = 0; j < n; j++)
            g.edges[i][j] = a[i][j];
}


int main ()
{
    //注意无向带权图i=j是为0
        int a[4][MAXV] = {{0, 1, 3, 1},
                          {1, 0, 2, 4},
                          {3, 2, 0, INF},
                          {1, 4, INF, 0}};
        MatGraph  g;

        InitMatGraph(g, a, 4, 5);

        Prim(g, 0);
        return 0;
}

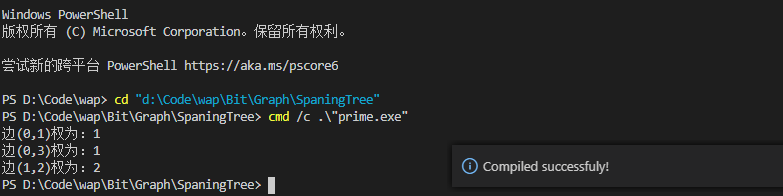
测试结果

Enjoy