Java 排序算法

Java 排序算法 - 为什么快速排序要比归并排序更受欢迎呢？

目录

• Java 排序算法 - 为什么快速排序要比归并排序更受欢迎呢？
  • 1. 归并排序
    • 1.1 工作原理
    • 1.2 三大指标
  • 2. 快速排序
    • 2.1 工作原理
    • 2.2 三大指标

数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html)

上一节分析了冒泡排序、选择排序、插入排序这三种排序算法，它们的时间复杂度都是 O(n²)，适合小规模数据排序。今天，本文继续分析两种时间复杂度为 O(nlogn) 的排序算法：归并排序和快速排序。这两种排序算法都用到分治思想，适合大规模数据排序，比上一节讲的那三种排序算法要更常用。

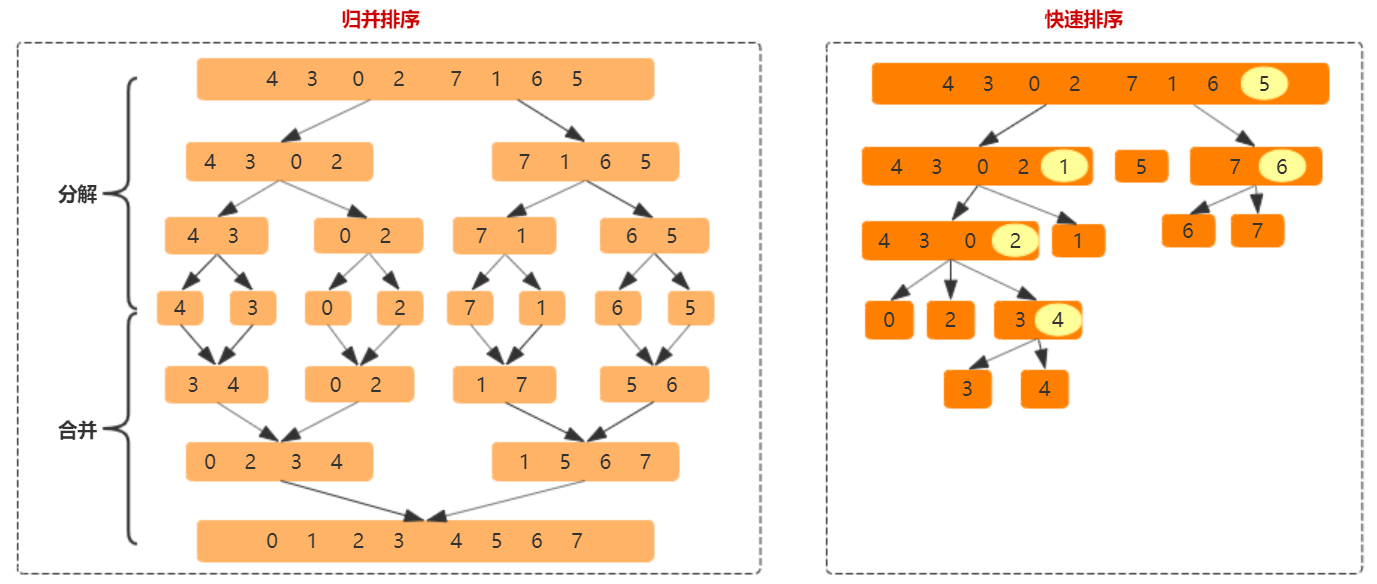
• 归并排序：将数列递归分解成只有一个元素。核心的算法是合并函数 merge：将两个有序数组合并后仍然有序。merge 函数决定了归并排序的空间复杂度和稳定性。
• 快速排序：任意选择一个元素作为分区占，分为小于，等于，大于三部分，然后依次对小于和大于部分递归排序。核心的算法是分区函数 partition：将数列分为左中右三部分。partition 函数同样决定了快速排序的空间复杂度和稳定性。

1. 归并排序

归并排序使用的就是分治思想，分治是一种解决问题的处理思想，递归是一种编程技巧。我们现在就来看看如何用递归代码来实现归并排序。

1.1 工作原理

把整个数列等分成两半：first, mid, last

1. 给 first 到 mid 部分排序（递归调用归并排序）
2. 给 mid + 1 到 last 部分排序（递归调用归并排序）
3. 归并这两个序列
4. 递归到足够小时，需要排列的数列只包含一个数，直接返回即可。倒数第二小的递归，是归并两个序列，每个序列各一个数。

递归公式：

# 对下标 p~r 之间的数组进行排序：arr[p] ~ arr[r]，其中 q=(p+r)/2 表示中间下标位置 
递推公式：mergeSort(p…r) = merge(merge_sort(p…q), mergeSort(q+1…r))
        
终止条件：p >= r 不用再继续分解

归并排序实现代码如下：

// 归并排序
public class MergeSort implements Sortable {
    @Override
    public void sort(Integer[] arr) {
        mergeSort(arr, 0, arr.length - 1);
    }

    /**
     * @param arr   要排序的数组
     * @param left  要排序数组的最小位置（包含）
     * @param right 要排序数组的最大位置（包含）
     */
    private void mergeSort(Integer[] arr, int left, int right) {
        if (left >= right) {
            return;
        }

        int middle = (left + right) / 2;
        mergeSort(arr, left, middle);
        mergeSort(arr, middle + 1, right);

        merge(arr, left, middle, right);
    }

    /**
     * 归并排序核心算法：合并两个有序数组，结果仍是有序。需要使用额外的数组空间，因此空间复杂度是 O(n)
     */
    private void merge(Integer[] arr, int left, int middle, int right) {
        // 为了避免频繁分配临时数组空间，可以将临时数组空间的开辟提前到sort方法中
        int[] tmpArray = new int[arr.length];

        int index = left;
        int leftIndex = left;
        int rightIndex = middle + 1;
        while (leftIndex <= middle && rightIndex <= right) {
            // 保证值相同时顺序不变
            if (arr[leftIndex] <= arr[rightIndex]) {
                tmpArray[index++] = arr[leftIndex++];
            } else {
                tmpArray[index++] = arr[rightIndex++];
            }
        }

        while (leftIndex <= middle) {
            tmpArray[index++] = arr[leftIndex++];
        }
        while (rightIndex <= right) {
            tmpArray[index++] = arr[rightIndex++];
        }

        index = left;
        while (index <= right) {
            arr[index] = tmpArray[index];
            index++;
        }
    }
}

1.2 三大指标

（1）时间复杂度

我们先感性认识分析一下归并排序的时间复杂度。归并排序分两层递归，外层递归使用二分法，时间复杂度为 logn，内层递归为合并两个有序数组，时间复杂度为 n，总的时间复杂度为 O(nlogn)。

下面理性分析归并排序的时间复杂度。归并排序递归的时间复杂度如下：

f(n) = 2*f(n/2)+n
     = 2*[2*f(n/4)+n/2]+n=4*f(n/4)+2*n
     = 4*[2*f(n/8)+n/4]+2*n=8*f(n/8)+3*n
     = 16*f(n/16)+4*n
     = ...
     = (2^logn)*f(n/(2^logn))+n*logn
     = n*f(1)+n*logn
所以时间复杂度为 O(n*logn)

（2）空间复杂度

merge 合并函数需要额外的空间进行临时合并数组的存储，即空间复杂度为 O(n)。

（3）稳定性

merge 合并函数通过比较相邻元素进行合并，相等元素的顺序没有发生改变，因此是稳定算法。

2. 快速排序

快速排序是 Hoare 在 1962 年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

2.1 工作原理

1. 每次选择任意分区点 key，通常选最前、最后、中间的元素值。如果元素是刚好全部逆序，最前或最后则会导致分区算法效率非常底下，一个好的办法是选择中间元素值作为分区点。
2. 每轮排序把比该数小的排在前边，大的排在后边。key 的位置就排好了。
3. 再对前半段和后半段递归使用快速排序。当排序的内容只有1到 2 个数时，一轮排序即可有序。

递归公式：

# 对下标 p~r 之间的数组进行排序：arr[p] ~ arr[r]，其中 q 表示分区点
递推公式：quickSort(p…r) = quickSort(p…q-1) + quickSort(q+1… r)
        
终止条件：p >= r 不用再继续分解

快速排序实现代码如下：

public class QuickSort implements Sortable {
    @Override
    public void sort(Integer[] arr) {
        quickSort(arr, 0, arr.length - 1);
    }

    private void quickSort(Integer[] arr, int left, int right) {
        if (left >= right) return;

        // 注意，middle 已经排序，不需要重新排序
        int middle = paritition(arr, left, right);
        quickSort(arr, left, middle - 1);
        quickSort(arr, middle + 1, right);
    }

    /**
     * 快速排序核心算法：分区算法，以任意元素为分区点 pivot，将小于等于 pivot 放到右边，大于 pivot 放到左边
     * 分区算法：1. 如果使用多个数组进行分区计算，虽然非常简单，但空间复杂度为 O(n)，和归并算法没有本质的提升
     *          2. 如果使用原地算法，空间复杂度为 O(1)，但也会导致相等元素乱序，是不稳定算法
     *
     * @param arr   要分区的数组
     * @param left  数组最小位置
     * @param right 数组最在位置
     * @return 中间值所有位置
     */
    private int paritition(Integer[] arr, int left, int right) {
        int pivot = arr[right];
        int i = left;
        for (int j = left; j < right; j++) {
            if (arr[j] <= pivot) {
                swap(arr, i, j);
                i++;
            }
        }
        swap(arr, i, right);
        return i;
    }

    private void swap(Integer[] arr, int i, int j) {
        if (i == j) return;
        int tmp = arr[j];
        arr[j] = arr[i];
        arr[i] = tmp;
    }
}

说明： 快速排序的核心是分区算法，本例中分区算法采用的是原地算法，也是空间复杂度为 O(1)。但这是牺牲稳定性换来的，由于存在非相邻元素的比较交换，相等元素的顺序会发生乱序。

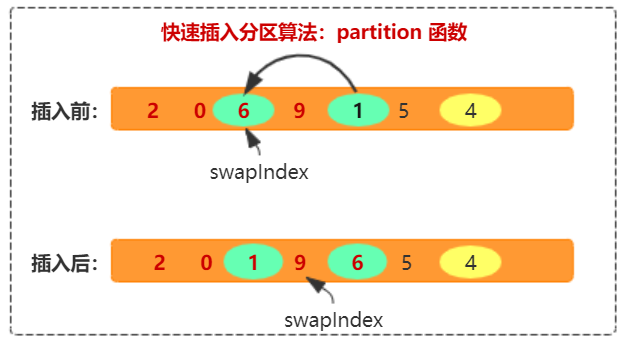
paritition 分区函数原理：和插入算法的思想类似，将数组分为两部分，已经处理部分和未处理部分。已处理部分，指小于和大于分区点的元素已经排序完成。然后循环将非处理部分的元素插入已经处理的部分，此时和插入算法不同，分区函数直接交换位置即可，不需要递归搬移元素。

如下图所示，有 "2 0 6 9 1 5 4" 数组有 7 个元素，分区点的值为 4，其中 "2 0 6 9" 为已经处理的部分（前两个元素都小于 4，后两个元素都大于 4），"1 5" 则是未处理部分。当处理 1 时，将 1 和 4 进行比较，由于小于 4，则会将 swapIndex 的元素和 元素1 直接交换位置，并且 swapIndex++。如果大于 4 ，比如 5 则不作任务处理。处理完成后数组会分为小于，大于分区点值的两部分。

这种分区算法属于原地算法，效率很高。同时也要思考一下，如果元素值也为 4 会怎么处理呢？我们也可以看出这各分区算法并不能保证值相等的元素有序性，属于不稳定算法。

2.2 三大指标

（1）时间复杂度

1. 最好情况：每次选的 key 值正好等分当前数列，递归 O(logn) 次，每次 i 移动的总长度是 O(n)，时间复杂度是 O(nlogn)。
2. 最坏情况：每次 key 值只分出 1 个元素在小端（或每次在大端），递归 n 次，每次 i 移动的总长度是 O(n)，时间复杂度 O(n²)。
3. 平均复杂度：O(nlogn)。

（2）空间复杂度

使用原来的数组进行排序，是原地排序算法，即 O(1)。

（3）稳定性

由于分区函数属于不稳定算法，所以快速排序也属性不稳定排序。

参考：

1. 排序动画演示：http://www.jsons.cn/sort/

---

每天用心记录一点点。内容也许不重要，但习惯很重要！