栈
栈的定义
栈(stack)是限定仅在表尾进行插入和删除操作的线性表。我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),没有任何数据元素的栈称为空栈。栈又称为后进先出(Last In First Out)的线性表,简称LIFO结构。
栈元素具有线性关系,及前驱和后继的关系。关于定义中仅在表尾插入和删除的操作,这里的表尾指的是栈顶。栈元素的特殊之处在于限制了插入和删除的位置,只能在栈顶进行,所以栈底是固定的,最先进栈的只能在栈底。

栈的抽象数据类型
Data:和线性表一样,元素具有相同类型,相邻的元素具有前驱和后继
Operation:
InitStack(*S):初始化操作,建立一个空栈S
DestroyStack(*S)若栈存在,则销毁它
ClearStack(*S)将栈清空
StackEmpty(S)若栈为空返回True.否则返回False
GetTop(S,*e)若栈存在并且非空,用e返回S的栈顶元素
Push(*S,e)若栈S存在,插入新元素e到栈S并称为栈顶元素
Pop(*S,*e)删除栈顶元素,并用e返回其值
StackLength(S)返回栈S的元素个数
栈的顺序存储结构实现
使用顺序结构存储的栈我们称为顺序栈,和线性表顺序存储结构的实现一样,我们采用数组的方式来实现顺序栈,使用数组中下标为0的一端作为栈底,我们定义一个Top变量来指示栈顶元素在数组中的位置,定义栈的长度为 Stacksize,则top<StackSize,当栈存在一个元素时,top为0,空栈的判断为top-1。
现有一个栈,Stacksize=5,则栈的示意图如下:

顺序栈的实现:
/**
* 基于数组实现的顺序栈
* @param <E>
*/
public class Stack<E> {
private Object[] data = null;
private int maxSize=0; //栈容量
private int top =-1; //栈顶指针
/**
* 构造函数:根据给定的size初始化栈
*/
Stack(){
this(10); //默认栈大小为10
}
Stack(int initialSize){
if(initialSize >=0){
this.maxSize = initialSize;
data = new Object[initialSize];
top = -1;
}else{
throw new RuntimeException("初始化大小不能小于0:" + initialSize);
}
}
//判空
public boolean empty(){
return top==-1 ? true : false;
}
//进栈,第一个元素top=0;
public boolean push(E e){
if(top == maxSize -1){
throw new RuntimeException("栈已满,无法将元素入栈!");
}else{
data[++top]=e;
return true;
}
}
//查看栈顶元素但不移除
public E peek(){
if(top == -1){
throw new RuntimeException("栈为空!");
}else{
return (E)data[top];
}
}
//弹出栈顶元素
public E pop(){
if(top == -1){
throw new RuntimeException("栈为空!");
}else{
return (E)data[top--];
}
}
//返回对象在堆栈中的位置,以 1 为基数
public int search(E e){
int i=top;
while(top != -1){
if(peek() != e){
top --;
}else{
break;
}
}
int result = top+1;
top = i;
return result;
}
}栈的链式存储结构实现
栈的链式存储结构,称为链栈。我们把栈顶放到单链表的头部,通常对链栈来说是不需要头结点。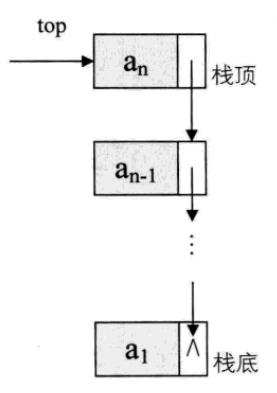
对于链栈来说一般不存在栈满的情况,除非内存没有可用空间了,对于空栈来说,链表原定义的是头指针指向空,那么链栈的空就是top=NULL
链栈的实现
public class LinkStack<E> {
//链栈的节点
private class Node<E>{
E e;
Node<E> next;
public Node(){}
public Node(E e, Node next){
this.e = e;
this.next = next;
}
}
private Node<E> top; //栈顶元素
private int size; //当前栈大小
public LinkStack(){
top = null;
}
//当前栈大小
public int length(){
return size;
}
//判空
public boolean empty(){
return size==0;
}
//入栈:让top指向新创建的元素,新元素的next引用指向原来的栈顶元素
public boolean push(E e){
top = new Node(e,top);
size ++;
return true;
}
//查看栈顶元素但不删除
public Node<E> peek(){
if(empty()){
throw new RuntimeException("空栈异常!");
}else{
return top;
}
}
//出栈
public Node<E> pop(){
if(empty()){
throw new RuntimeException("空栈异常!");
}else{
Node<E> value = top; //得到栈顶元素
top = top.next; //让top引用指向原栈顶元素的下一个元素
value.next = null; //释放原栈顶元素的next引用
size --;
return value;
}
}
}如果在栈的使用过程中元素变化不可预料,有时大有时小,那么最好采用链栈,反之变化在可控范围内使用顺序栈。
两栈共享空间
如果有两个类型相同的栈,我们为它们分别开辟了数组空间。极有可能是一个栈已经满了,再入栈就溢出了,而另一个栈却还有很多存储空间。这又何必呢?我们完全可以用一个数组来存储两个栈,只不过需要一些小的技巧。
我们的做法如下,数组有两个端点,两个栈有两个栈底。让一个栈的栈底为数组的始端,即数组下标为0的位置。让另一个栈的栈底为数组的末端,即数组下标为n-1的位置。这样如果两个栈增加元素,就是两端点向中间延伸。
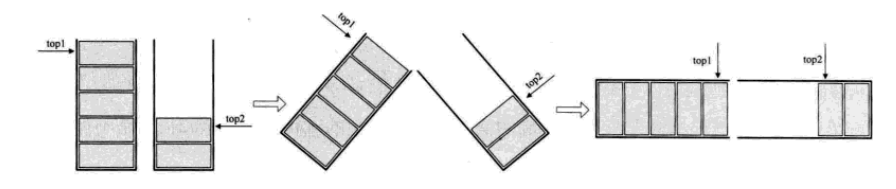
其实关键思路是:它们是在数组的两端,向中间靠拢。top1和top2是两个栈的栈顶指针。只要它们两个不见面,两个栈就可以一直使用。
代码实现:
/**
* 两栈共享空间
* @author Administrator
*
*/
public class BothStack <T>{
private Object[] element; //存放元素的数组
private int stackSize; // 栈大小
private int top1; //栈1的栈顶指针
private int top2; //栈2的栈顶指针
/**
* 初始化栈
* @param size
*/
public BothStack(int size){
element = new Object[size];
stackSize = size;
top1 = -1;
top2 = stackSize;
}
/**
* 压栈
* @param i 第几个栈
* @param o 入栈元素
* @return
*/
public boolean push(int i , Object o){
if(top1 == top2 - 1)
throw new RuntimeException("栈满!");
else if(i == 1){
top1++;
element[top1] = o;
}else if(i == 2){
top2--;
element[top2] = o;
}else
throw new RuntimeException("输入错误!");
return true;
}
/**
* 出栈
* @param i
* @return
*/
@SuppressWarnings("unchecked")
public T pop(int i){
if(i == 1){
if(top1 == -1)
throw new RuntimeException("栈1为空");
return (T)element[top1--];
} else if(i == 2){
if(top2 == stackSize)
throw new RuntimeException("栈2为空");
return (T)element[top2++];
} else
throw new RuntimeException("输入错误!");
}
/**
* 获取栈顶元素
* @param i
* @return
*/
@SuppressWarnings("unchecked")
public T get(int i){
if(i == 1){
if(top1 == -1)
throw new RuntimeException("栈1为空");
return (T)element[top1];
} else if(i == 2){
if(top2 == stackSize)
throw new RuntimeException("栈2为空");
return (T)element[top2];
} else
throw new RuntimeException("输入错误!");
}
/**
* 判断栈是否为空
* @param i
* @return
*/
public boolean isEmpty(int i){
if(i == 1){
if(top1 == -1)
return true;
else
return false;
} else if(i == 2){
if(top2 == stackSize)
return true;
else
return false;
} else
throw new RuntimeException("输入错误!");
}
/**
* 遍历
*/
@SuppressWarnings("unchecked")
@Override
public String toString(){
String str1 = "栈1:[";
String str2 = "栈2:[";
for(int i=top1;i>=0;i--){
if(i == 0)
str1 = str1 + (T)element[i];
else
str1 = str1 + (T)element[i] + ",";
}
str1 += "]";
for(int i=top2;i<stackSize;i++){
if(i == stackSize-1)
str2 = str2 + (T)element[i];
else
str2 = str2 + (T)element[i] + ",";
}
str2 += "]";
return str1 + "
" + str2;
}
}
栈的应用一:递归
我们通常使用的递归就是栈来实现的,简单说我们递归前行阶段,我们将每一次的递归,函数的局部变量,参数值及返回地址压入栈中,在退回阶段再把压入的值给弹出,用于返回调用层次中执行代码的其余部分,也就是恢复了之前调用的状态。
栈的应用二:四则运算表达式(后缀表达式)
计算机中计算带括号的四则运算采用的是后缀表达式,后缀表达式就是所有的运算符都出现在要运算数字的后面出现。
对于9+(3-1)*3+10/2,后缀表达式的方法为“9 3 1 - 3 * + 10 2 / +” ,后缀表达式的计算方法,从左到右遍历表达式的每个符号和数字,遇到数字就进栈,遇到符号就将栈顶的两个数字出栈,进行计算,将运算结果进栈,一直到获得最终结果。
1.初始化一个空栈,因为前三个都是数字,就将 9 3 1入栈,如图:
 :
:
2.下面是“-” ,所以将1出栈作为减数,3出栈作为被减数,运算得到结果2,将2入栈,然后后面是数字3.入栈,如图:

3.后面是*号,将3 2 出栈相乘,得到结果6入栈,下面是+号将6和9出栈相加,得到15入栈,如图:

4.接下来数字10和2入栈,继续遇见符号号,栈顶10 与2出栈相除得到5.将5入栈,如图:

5.最后符号为+,将15和5出栈 相加得到20并入栈,最后20出栈得到最终结果,如图:

下面我们推导如何将标准四则运算(中缀表达式,因为符号都在中间)转化成后缀表达式:
从左到右遍历所有的字符和数字,若是数字就输出,成为后缀表达式的一部分,若是符号,则判断其与栈顶符号的优先级,是右括号或者优先级低于栈顶符号(先乘除后加减)则 将栈顶元素依次出栈并输出,并将当前符号进栈,一直到最后输出后缀表达式。
1.初始化空栈,用来对符号进行出入栈,如图:

2.第一个字符为9,输出,后面符号为“+”,则入栈。第三个符号是“(”,因为只是左括号还未配对,依旧进栈,下面符号是数字3,输出,这是表达式为 9 3 ,接着是“-”,则进栈。如图:

3.接下来数字1,表达式当前为 9 3 1,后面符号为“)”,此时需要匹配前面的左括号,所以栈顶依次出栈并输出,直至左括号出栈,此时左括号上只有“-”号,因此此时表达式为9 3 1 - ,接着是数字3 输出,表达式为 9 3 1 - 3 ,下面是*号,此时栈顶符号为+号,优先级低于*号,所以不输出并将*号入栈,如图:

4.之后是符号 +,当前栈顶符号为*号,优先级比+号高,因此栈中元素出栈并输出(因为没有比+号更低的优先级,所以全部出栈),表达式为9 3 1 - 3 * + ,然后将下面的符号+入栈,下面是数字10输出,表达式为9 3 1 - 3 * + 10 ,下一个符号是/入栈,如图:

5.最后一个数字2,输出表达式为9 3 1 - 3 * + 10 2,因为已经到最后将所以符号出栈并输出,表达式为9 3 1 - 3 * + 10 2 / + ,如图:

将中缀表达式转为后缀表达式(栈用来进出运算的符号),将后缀表达式运算出结果(栈用来进出运算的数字)