信息熵
信息熵也被称为熵,用来表示所有信息量的期望。
公式如下:

例如在一个三分类问题中,猫狗马的概率如下:
| label | 猫 | 狗 | 马 |
|---|---|---|---|
| predict | 0.7 | 0.2 | 0.1 |
| 信息量 | -log(0.7) | -log(0.2) | -log(0.1) |
信息熵为:H = −(0.5∗log(0.5)+0.2∗log(0.2)+0.3∗log(0.3))
针对二分类问题可以简写如下:
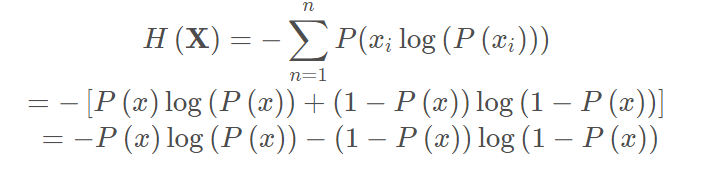
相对熵(KL散度)
如果对于同一个随机变量X,有两个单独的概率分布P(x)和Q(x),则我们可以使用KL散度来衡量这两个概率分布之间的差异。
用来表示两个概率分布的差异
公式如下:
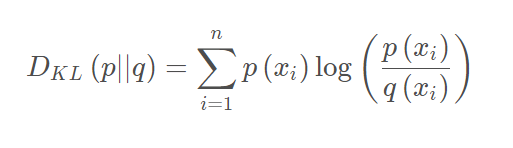
# pytorch代码
kl_loss = torch.nn.KLDivLoss()
kl_loss_output = klloss(logit1, logit2)
例如在一个三分类问题中,概率如下:
| 猫 | 狗 | 马 | |
|---|---|---|---|
| label | 1 | 0 | 0 |
| predict | 0.7 | 0.2 | 0.1 |
则KL散度如下:

交叉熵(CE, Cross Entropy)
交叉熵 = KL散度 + 信息熵,常作为损失函数来最小化KL散度,且计算比KL散度简单。
常用于计算label和概率之间的差异,计算量比KL散度小
公式如下(可以通过上文信息熵和KL散度推导):
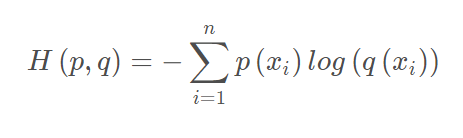
# pytorch代码
crossentropy_loss = torch.nn.CrossEntropyLoss()
crossentropy_loss_output = crossentropyloss(label, predict)
举例如下:
| 猫 | 狗 | 马 | |
|---|---|---|---|
| label | 1 | 0 | 0 |
| predict | 0.7 | 0.2 | 0.1 |
那么loss计算公式如下:
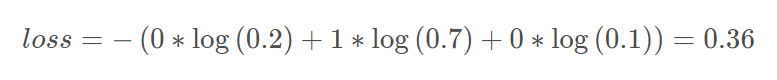
和MSE对比:当使用sigmoid作为激活函数的时候,常用交叉熵损失函数而不用均方误差损失函数,因为它可以完美解决平方损失函数权重更新过慢的问题,具有“误差大的时候,权重更新快;误差小的时候,权重更新慢”的良好性质。
和方差(SSE)
和方差用来计算两个概率分布之间的差异,计算公式如下:
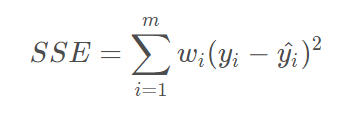
均方差(MSE)
均方差也用来计算两个概率分布之间的差异,计算公式如下:
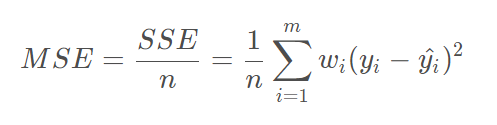
# pytorch代码
mse_loss = torch.nn.MSELoss(reduce=True, size_average=True)
mse_loss_output = mse_loss(logit1, logit2)
还是拿三分类问题举例:
| 猫 | 狗 | 马 | |
|---|---|---|---|
| label | 1 | 0 | 0 |
| teacher_pre | 0.7 | 0.2 | 0.1 |
| student_pre | 0.6 | 0.2 | 0.2 |
那么mse loss = [(0.7-0.6)^2 + (0.2-0.2)^2 + (0.1-0.2)^2] / 3
均方根误差(RMSE)
也叫回归系统的拟合标准差,是MSE的平方根,计算公式如下:
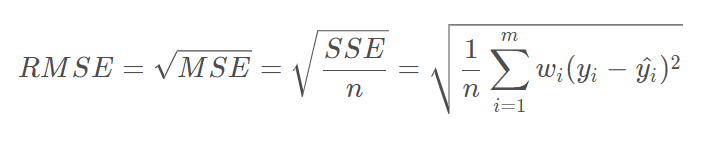
SSE、MSE、RMSE三者比较相似,其中MSE常用于模型蒸馏中,用于计算student和teacher的logit之间的概率分布差异
Hinge损失函数
专用于二分类的损失函数,公式如下:
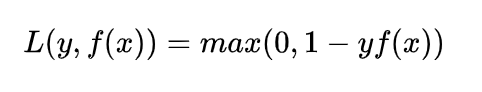
SVM使用的损失函数,如果分类正确,则loss为0,否则损失为1-yf(x),其中1可以作为一个超参数设置为其他值
其中|f(x)|<=1,y是目标值1或者-1