[ZJOI2007]矩阵游戏

题目描述

小Q是一个非常聪明的孩子，除了国际象棋，他还很喜欢玩一个电脑益智游戏――矩阵游戏。矩阵游戏在一个N*N黑白方阵进行（如同国际象棋一般，只是颜色是随意的）。每次可以对该矩阵进行两种操作：

行交换操作：选择矩阵的任意两行，交换这两行（即交换对应格子的颜色）

列交换操作：选择矩阵的任意两列，交换这两列（即交换对应格子的颜色）

游戏的目标，即通过若干次操作，使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。

对于某些关卡，小Q百思不得其解，以致他开始怀疑这些关卡是不是根本就是无解的！！于是小Q决定写一个程序来判断这些关卡是否有解。

输入输出格式

输入格式：

第一行包含一个整数T，表示数据的组数。

接下来包含T组数据，每组数据第一行为一个整数N，表示方阵的大小；接下来N行为一个N*N的01矩阵（0表示白色，1表示黑色）。

输出格式：

包含T行。对于每一组数据，如果该关卡有解，输出一行Yes；否则输出一行No。

输入输出样例

输入样例#1：

2
2
0 0
0 1
3
0 0 1
0 1 0
1 0 0

输出样例#1：

No
Yes

说明

对于20%的数据，N ≤ 7

对于50%的数据，N ≤ 50

对于100%的数据，N ≤ 200

也许有人一开始看到题目就想到搜索？？    

但一想到搜索就有点.............不爽........

说一下正解。

其实这是一道二分图匹配的问题。

关键在于建模，如果（i,j）点所给出的点值为1的话，那我们就建一条从i到j的边，建完边后就进行二分图匹配，如果可以完全匹配（即全部匹配数为n），则方阵的主对角线是可以全为黑色的，否则不能。

为什么呢？

我们可以手工模拟一下，比如说样例的第二个测试数据。

根据我上面说的，我们会建这几条边：

       

然后，我们将矩阵的第一行和第二行交换下试试？？

得到下面的图片：

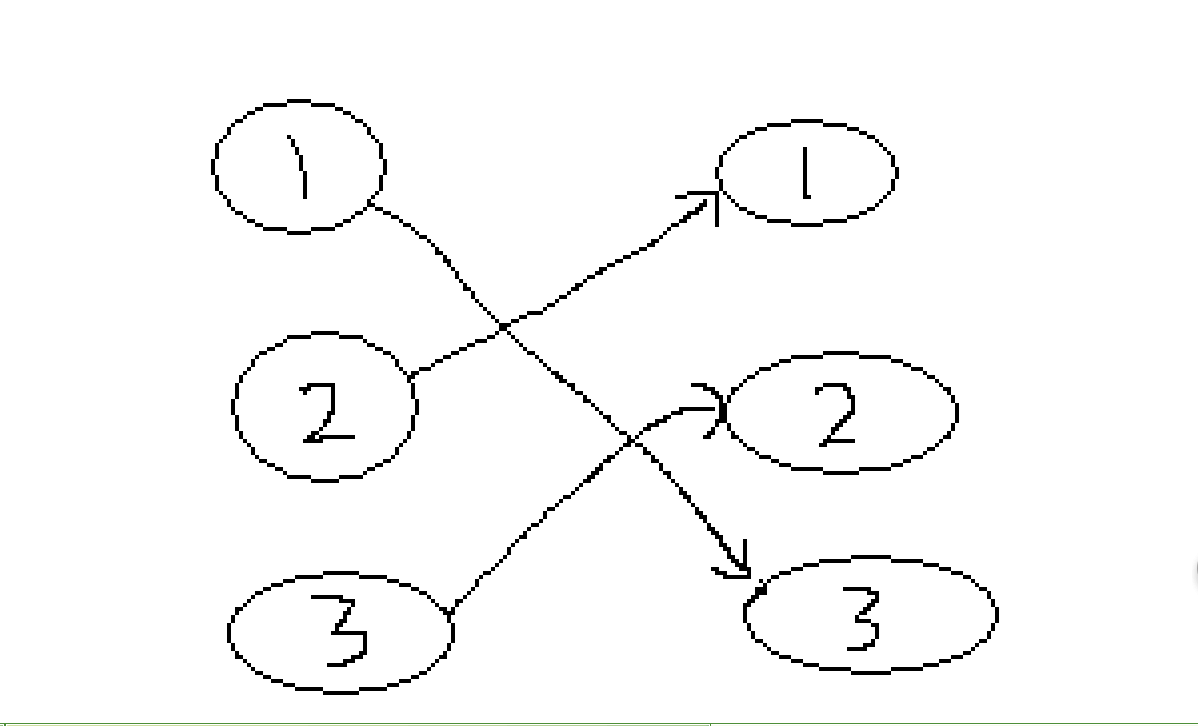
发现交换后的图片有什么差别？？

其实只是将第一张图片右边的一二两点交换，然后重新编号而已，其他还是不变的！！

我们再看一看这个测试点的最终状态：

1 0 0

0 1 0

0 0 1

对应的图为：

最后状态是图是一对一的，所以从上面我们就可以知道，其实只要建的图能完全匹配就行，因为无论是交换行还是列，都是不会改变匹配数的。

恩，下面贴代码，有问题下面留言。

#include<cstdio>
#include<cstring>
#define N 210
using namespace std;

int match[N][N];
int result[N];
bool use[N];
int n;

bool dfs(int now){
    for(int b = 1; b <= n; b++)
      if(!use[b] && match[now][b]){
          use[b] = true;
          if(!result[b] || dfs(result[b])){
              result[b] = now;
              return true;
          }
      }
    return false;
}

bool xiongyali(){
    memset(result,0,sizeof(result));
    int ans = 0;
    for(int a = 1; a <= n; a++){
        memset(use,0,sizeof(use));
        if(dfs(a))ans++;
    }
    if(ans == n)return true;
    else return false;
}

int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        memset(match,0,sizeof(match));
        scanf("%d",&n);
        for(int i = 1; i <= n; i++)
           for(int j = 1; j <= n; j++)
                 scanf("%d",&match[i][j]);
        if(xiongyali())printf("Yes
");
        else printf("No
");
    }
    return 0;
}