（基础）--- 动态规划 --- 线性、背包、区间

一、斐波那契

递归

1. 代码虽然简洁、但是低效。时间复杂度为O（2^n）
2. 递归算法时间复杂度计算：子问题个数乘以解决一个子问题需要的时间

int fib(int N) {
      if (N == 1 || N == 2) return 1;
      return fib(N - 1) + fib(N - 2);
}

观察递归树，存在大量的重复计算，导致低效

记忆化搜索

用数组等将已经算过的东西记录下来，在下一次要使用的时候，直接用已经计算过的值，避免重复计算，去掉重复的搜索树

递推

f[0] = f[1] = 1;
for(int i = 2; i <= n; i ++ ){
    f[i] = f[i - 1] + f[i - 2];
}
return f[n];

相关例题

三步问题

类似于斐波那契数列，采用递推的方式，记得加上long long，防止爆int.
假设我们在第i阶阶梯上，上一步在i-1阶或者i-2阶或者i-3阶，根据分类加法原理
f[i] = (f[i - 3] + f[i - 2] + f[i - 1])
求到第1、2、3阶梯的时候，显然f[1] = 1,f[2] = 2,f[3] = 4

class Solution {
public:
    const int mod = 1000000007;
    long long f[1000010];
    int waysToStep(int n) {
       f[1] = 1,f[2] = 2,f[3] = 4;
       for(int i = 4; i <= n; i ++ ){
           f[i] = (f[i - 3] + f[i - 2] + f[i - 1]) % mod;
       }
       return f[n];
    }
};

动态规划原理——加法原理

分类加法原理

做一件事，完成它可以有n类方法，在第一类方法中有m1种不同的方法，在第二类方法中有m2种不同的方法，……，在第n类方法中有mn种不同的方法，那么完成这件事共有N = m1 + m2 + m3 + ... + mn种不同方法。

分步乘法原理

做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法，那么完成这件事共有N = m1 * m2 * m3 * ... * mn种不同的方法。

动态规划的若干个定义：

• 动态规划是解决多阶段决策过程最优化问题的一种方法
• 阶段：把问题分成几个相互联系的有顺序的几个环节，这些环节即称为阶段
• 状态：某一阶段的出发位置称为状态，通常一个阶段包含若干状态
• 决策：从某阶段的一个状态演变到下一个阶段某状态的选择
• 策略：从开始到终点的全过程，由每段决策组成的决策序列称为全过程策略，简称策略
• 状态转移方程：由前一阶段到后一阶段演变规律，i阶段到i + 1阶段状态

动态规划适用的基本条件

具有相同子问题

1. 首先，我们必须保证这个问题能够分解出几个子问题，并且能够通过这些子问题解决
2. 其次，将这些子问题作为一个新问题，它也能分解成为相同的子问题进行描述

满足最优子结构

1. 问题的最优解包含着它的子问题的最优解。不管前面的策略如何，此后的决策必须是基于当前状态（由上一次决策产生）的最优决策

满足无后效性

1. 明动态规划只适用于解决当前决策与过去状态无关的问题。状态，出现在策略任何一个位置，它的地位相同，都可实施同样策略，这就是无后效性的内涵.
2. 如果当前问题的具体决策，会对解决其它未来的问题产生影响，如果产生影响，就无法保证决策的最优性。

动态规划分析步骤

1. 结合原问题和子问题确定状态
   • 题目在求什么？要求出这个值我们需要知道什么？什么是影响答案的因素？
   • （一维描述不完就二维，二维不行就三维四维。）
   • 状态的参数一般有
   • 1）描述位置的：前(后)i单位，第i到第j单位，坐标为(i,j)，第i个之前（后）且必须
   取第i个等
   • 2）描述数量的：取i个，不超过i个，至少i个等
   • 3）描述对后有影响的：状态压缩的，一些特殊的性质

2. 确定转移方程
   • 1）检查参数是否足够；
   • 2）分情况：最后一次操作的方式，取不取，怎么样取——前一项是什么
   • 3）初始边界是什么。
   • 4）注意无后效性。比如说，求A就要求Ｂ，求Ｂ就要求Ｃ，而求Ｃ就要求Ａ，这就
   不符合无后效性了。
   根据状态枚举最后一次决策（即当前状态怎么来的）就可确定出状态转移方程！

3.考虑是否需要优化

4.确定编程实现方式
• 1）递推
• 2）记忆化搜索

例题：

练习一：传球游戏

代码如下：

#include<iostream>

using namespace std;

const int N = 100;

/*
有多少种不同的传球方法
可以使得从小蛮手里开始传的球，
传了m次以后，又回到小蛮手里。

原问题：第1号传m次到第1号 
子问题：第1号传i次到第j号手里面 

状态转移方程：f[i][j] = f[i - 1][j + 1] + f[i - 1][j - 1];
初始化：f[0][1] = 1 
环：j = 1 , j - 1 = n
	j = n,  j + 1 = 1 

*/

int n,m;
int f[N][N];

int main() {
	cin >> n >> m;
	f[0][1] = 1;
	for(int i = 1; i <= m; i ++ ){
		for(int j = 1; j <= n; j ++ ){
			if(j == 1) f[i][j] = f[i - 1][j + 1] + f[i - 1][n];
			else if(j == n) f[i][j] = f[i - 1][1] + f[i - 1][j - 1];
			else f[i][j] = f[i - 1][j + 1] + f[i - 1][j - 1];
		}
	}
	cout<<f[m][1];
	return 0;
}

[练习二：最长上升子序列(LIS)]（https://leetcode-cn.com/problems/longest-increasing-subsequence/submissions/）

代码如下：

#include<iostream>

using namespace std;

const int N = 1010;

/*
原问题：整个数列（1-N）的单调递增的子序列（不连续）最长的长度
子问题：以i结尾的单调递增的最长长度 

转移方程：f[i] = max(f[j] + 1,f[i])(a[j] < a[i], j < i)

初始化：f[1 ~ n] = 1 (每个a[i]自身长度为1) 
 
样例:
5
4 2 3 1 5
输出：3 

*/
int n;
int a[N];
int f[N];

int main() {
	cin >> n;
	for(int i = 1; i <= n; i ++ ){
		cin >> a[i]; 
	}
	int res = 0;
	for(int i = 1; i <= n; i ++ ){
		f[i] = 1; 
		for(int j = 1; j < i; j ++ ){
			if(a[j] < a[i]){
				f[i] = max(f[j] + 1,f[i]);
			}
		}
		res = max(f[i],res);
	}
	cout<<res;
	return 0;
}

[练习三：滑雪]（https://ac.nowcoder.com/acm/problem/105685）

代码如下：

1. 动态规划做法，记忆化搜索

#include<iostream>

using namespace std;

const int N = 110;

/*

原问题：从(1,1)~(n,m)的任意一点下滑最长的长度
子问题：从(i,j)下滑最长的长度

状态转移：从某个点滑向上下左右相邻四个点之一

转移方程: f[i][j] = f[i - 1][j] + 1 (a[i - 1][j] < a[i][j])
		  f[i][j] = f[i + 1][j] + 1 (a[i + 1][j] < a[i][j])
		  f[i][j] = f[i][j - 1] + 1 (a[i][j - 1] < a[i][j])
		  f[i][j] = f[i][j + 1] + 1 (a[i][j + 1] < a[i][j])

初始化：f[i][j] = 1;

*/

int n,m;
int a[N][N],f[N][N];

int find(int i,int j) {
	if(f[i][j]) return f[i][j];
	f[i][j] = 1;
	if(i > 1 && a[i - 1][j] < a[i][j])
		f[i][j] = max(find(i - 1,j) + 1,f[i][j]);
	if(i < n && a[i + 1][j] < a[i][j])
		f[i][j] = max(find(i + 1,j) + 1,f[i][j]);
	if(j > 1 && a[i][j - 1] < a[i][j])
		f[i][j] = max(find(i,j - 1) + 1,f[i][j]);
	if(j < m && a[i][j + 1] < a[i][j])
		f[i][j] = max(find(i,j + 1) + 1,f[i][j]);
	return f[i][j];
}
int main() {
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) {
		for(int j = 1; j <= m; j ++ ) {
			cin >> a[i][j];
		}
	}
	int res = 0;
	for(int i = 1; i <= n; i ++ ) {
		for(int j = 1; j <= m; j ++ ) {
			res = max(res,find(i,j));
		}
	}
	cout<<res;
	return 0;
}

2. DFS搜索，用st数组标记并且记录最长路径

#include<iostream>

using namespace std;

const int N = 110;

/*

*/

int n,m;
int g[N][N];
int st[N][N]; //用st数组记录从此点出发的最长路径长度 
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};

int ans;

int dfs(int x,int y){
	if(st[x][y]) return st[x][y];
	//初始路径长度为1 
	int u = 1;
	//上下左右 
	for(int i = 0; i < 4; i ++ ){
		int a = x + dx[i];
		int b = y + dy[i];
		if(a < 1 || a > n || b < 1 || b > m || g[a][b] >= g[x][y]) continue;
		u = max(u,dfs(a,b) + 1);
	}
	//记录从(x,y)出发的最长路径长度 
	st[x][y] = u;
	//更新路径长度 
	ans = max(ans,u);
	return u;
}
int main() {
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ){
		for(int j = 1; j <= m; j ++ ){
			cin >> g[i][j];
		}
	}	
	for(int i = 1; i <= n; i ++ ){
		for(int j = 1; j <= m; j ++ ){
			dfs(i,j);
		}
	}
	cout<<ans;
	return 0;
}

练习四：最大子串和

给你一个有正有负的序列，求一个子串（连续的一段），使其和最大！

代码如下：

#include<iostream>

using namespace std;

const int N = 110;

/*
原问题：求(1 ~ n)中最大字串和 
子问题：前i个数的最大子串和 

转移方程:f[i] = f[i - 1] + a[i];

初始化为:f[i] = a[i];
 
输入： 
6 
-5 6 -1 5 4 -7
输出：
14
 
*/
int n,a[N],f[N];

int main() {
	cin >> n;
	for(int i = 1; i <= n; i ++ ) cin >> a[i];
	int res = -1e9;
	for(int i = 1; i <= n; i ++ ){
		f[i] = a[i];
		f[i] = max(f[i],f[i - 1] + a[i]);
		res = max(res,f[i]);
	}
	cout<<res;		
	return 0;
}

练习五：最长公共子序列(LCS)

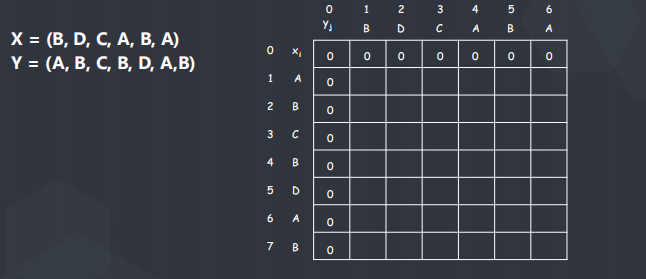
代码如下:
1.非接口

#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;

const int N = 1010;

/*
原问题：两个字符串中最长公共子序列 

状态表示：f[i][j]表示前一个字符串的第i位与后一个字符串的前j位的最长公共子序列长度 

转移方程：
如果s1[i] == s2[j] ：f[i][j] = f[i - 1][j - 1] + 1; 
	s1[i] != s2[j] : f[i][j] = max(f[i - 1][j],f[i][j - 1]);

输入： 
4 4
abcd becd

输出：
3("bcd") 
*/
int n,m;
char s1[N],s2[N];
int f[N][N];

int main() {
	cin >> n >> m;
	scanf("%s %s",s1 + 1,s2 + 1);		
	for(int i = 1; i <= n; i ++ ){
		for(int j = 1; j <= m; j ++ ){
			if(s1[i] == s2[j]){
				f[i][j] = f[i - 1][j - 1] + 1;
			}else{
				f[i][j] = max(f[i - 1][j],f[i][j - 1]);
			}
		}
	}
	cout<<f[n][m];
	return 0;
}

2.接口

class Solution {
public:
    int f[1010][1010];
    int longestCommonSubsequence(string s1, string s2) {
        int n = s1.size(),m = s2.size();
        for(int i = 1; i <= n; i ++ ){
            for(int j = 1; j <= m; j ++ ){
                if(s1[i - 1] == s2[j - 1]){
                    f[i][j] = f[i - 1][j - 1] + 1;
                }else{
                    f[i][j] = max(f[i - 1][j],f[i][j - 1]);
                }
            }
        }
        return f[n][m];
    }
};