BZOJ 2122 [分块+单调栈+二分]（有详解）

题面

传送门

给定序列d和lim。假设有一个初始价值(x_0)，则经历第i天后价值变为(min(x_0+d[i],lim[i]))，记(f(i,j,x_0))表示以初始代价x0依次经过第i天到第j天后的价值。每次询问给出(l,r,x0)，求(max(f(i,j,x_0)))，其中[i,j]是子串[l,r]的子串（连续）。

分析

暴力

首先有个暴力的做法

每次询问DP一次，设dp[i]表示从询问左端点l到第i天结束的答案

则(dp[i]=min(max(dp[i-1],x_0)+d[i],lim[i])),正确性显然，max表示两种情况，一种是从前一天继续转移，一种是从第i天重新开始

该算法的时间复杂度为(O(nm))

---

特殊性质

那么如何优化呢？我们发现f函数满足很特殊的性质

1.若(ageq b)则$f(l,r,a) geq f(l,r,b) $

证明：如果会被取min导致最终结果小于x0,则无论初始值是a或者是b都是一样的。如果不会被取min，则从a开始累加显然会更大一些

我们可以把被取min形象的想象成通过一个空隙被卡住，无论多大都会被卡成lim[i]

2.设(g(l,r)=f(l,r,+∞), s(l,r)=sum_{i=l}^{r}d_i)则(f(l,r,x_0)=min(g(l,r),s(l,r)+x_0))

证明:

如果被取min,则无论(x_0)多大都会被卡住，所以最后得到的值跟(x_0)无关，答案为(g(l,r))

如果没被取min，则答案就是所有的d[i]累加，再加上初始值，显然是(s(l,r)+x_0)),根据性质1,(f(l,r,+∞) geq f(l,r,x_0))，即(g(l,r) geq (s(l,r)+x_0))，两个值中的最小值即为答案

举个栗子：

d	-5	8	6	7	9
lim	5	4	2	4	10

如果查询l=2,r=3,x0=1，显然答案会和4取min,只会<=4,被卡住了

最优方案为第二天工作一天，得到的最大值为4

此时g(l,r)=4，s(l,r)=7,两者取min即为答案

---

分块预处理

那么如何分块？

考虑在每个块内暴力dp,求出每个区间的g值，第i个块中g(l,r)记为(g[i][l][r])，为了避免数组越界，l,r存储时的下标需要减去块的左端点

s值用一个前缀和处理就可以了

然后将每个块(编号id)中的g,s值存入三个vector(每个块都有3个),vblock,vleft,vright

vblock[id]存当前块内值，即(g(i,j),s(i,j) (i leq j 且i,j in [l,r]))

vright[id]存以当前块中位置为终点的值，相当于查询时最右边的一小块，即(g(l,i),s(l,i) (i in [l,r]))
vleft[id]存以当前块中位置为起点的值，相当于查询时最左边的一小块,即(g(i,r),s(i,r) (i in [l,r]))

为什么要这样存储呢，因为我们查询时要分别求vblock,vright,vleft里的最大值，即(max( min(g(i,j),s(i,j)+x_0)),(g(i,j),s(i,j)) in vblock[id])

显然我们需要快速求一个vector中的(max( min(g(i,j),s(i,j)+x_0)))。如果g,s有单调性，我们就可以二分求出最大值点了，所以我们要想办法把序列变单调,并且排除多余情况

首先我们对于vector中的每一个数对(g,s)，我们先按照g从小到大排序，g相同时按照s从小到大排序

发现若存在((g_1,s_1),(g_2,s_2))使得(g_1>s_1,g_2>s_2),则选((g_1,s_1))显然更优

因此我们维护一个单调栈，依次将vector中的元素入栈，保证栈中元素的s值从大到小递减，栈顶s最小。此时由于排序保证了g单调递增，所以每次入栈时弹出的数一定不优。

然后从栈顶到栈底依次弹出元素，插回原vector，由于现在把序列逆序，此时g单调递减，s单调递增

然后就可以二分了，如下图所示：

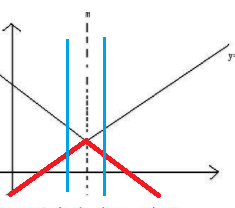
递减的直线是g,递增的直线是s+x0,红线为min(g,s+x0)，显然交点处有最大值。但由于交点可能不是整点，所以我们二分找出最后一个g>s+x0的位置（蓝线）ans,把ans和ans+1处的最大值取min即可

查询

不完整块直接暴力，对于一个完整块，有几种选择

1.从本块开始，从本块结束 （用vblock[id]中的最大值)
2.从本块开始，走到块尾 （用vleft[id]中的最大值）
3.从前面的块走过来，从本块结束 （用vright[id]中的最大值）
4.从这一块前面开始走到这一块后面，不在本块结束
5.不走这一块（和x0取min)

具体不太好描述，还是看代码实现

long long query(int l,int r,long long x0){//查询l,r,x0
	long long ans=x0,tmp;//tmp为从l到当前位置的答案 ,ans表示目前最优答案
	tmp=x0;
	for(int i=l;i<=min(rb(id[l]),r);i++){//不完整块的暴力
		tmp=min(max(tmp,x0)+d[i],lim[i]);
		ans=max(ans,tmp);
	}
	for(int i=id[l]+1;i<id[r];i++){
		ans=max(ans,find_mpos(vright[i],tmp));
        //find_mpos(v,x0)是按上述方法求v中最大值，且加上x0
        //从前面的块走过来，从本块结束，把tmp当成x0传进去，相当于把这块之前的答案也累计进去，再加上v里面的部分即是从前面到本块的答案
		ans=max(ans,find_mpos(vblock[i],x0));
        //从本块开始，从本块结束
		tmp=min(get_g(lb(i),rb(i)),get_s(lb(i),rb(i))+tmp);
        //从这一块前面开始走到这一块后面，不在本块结束，所以不更新ans,把本块的g值和s值累计入tmp
		tmp=max(tmp,find_mpos(vleft[i],x0));
        //从本块开始，走到块尾
        
        //从这一块前面开始走到这一块后面，不在本块结束这种情况的值已经存在tmp里了，等到了结束的地方再更新ans,这里不用写
	}
	if(id[l]!=id[r]){
		for(int i=lb(id[r]);i<=r;i++){//不完整块的暴力
			tmp=min(max(tmp,x0)+d[i],lim[i]);
			ans=max(ans,tmp);
		}
	}
	return ans;
}

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<stack>
#include<queue>
#include<vector>
#include<cmath>
#define INF 0x3f3f3f3f
#define maxn 50005
#define maxs 225
#define maxb 305
using namespace std;
struct val{
	long long g;
	long long s;
	val(){
		
	}
	val(long long _g,long long _s){
		g=_g;
		s=_s;
	}
	friend bool operator < (val p,val q){
		if(p.g==q.g) return p.s<q.s;
		else return p.g<q.g;
	}
};
int n,m;
int sz;
int cnt;
long long d[maxn],lim[maxn]; 
long long g[maxs][maxs][maxs];
//g[i][l][r]表示第i块中[l,r]区间的g值，其中l,r是块内坐标，实际下标要加上lb(i) 
long long sum[maxn];//前缀和
int id[maxn];//id[i]表示第i个位置属于第几个块
inline int lb(int id){//lb(id),rb(id)为第i个块的左右边界
	return (id-1)*sz+1;
}
inline int rb(int id){
	return id*sz>=n?n:id*sz;
}
inline long long get_s(int l,int r){
	return sum[r]-sum[l-1];	
}
inline long long get_g(int l,int r){
	int k=id[l];
	return g[k][l-lb(k)][r-lb(k)];
}

vector<val>vblock[maxb],vright[maxb],vleft[maxb];
//vblock存当前块内g值
//vright存以当前块中位置为终点的值，查询时右边多出部分 
//vleft存以当前块中位置为起点的值，查询时左边多出部分 
void del_small(vector<val> &in){
	sort(in.begin(),in.end());
	stack<val>s; //单调栈
	for(int i=0;i<in.size();i++){
		while(!s.empty()&&s.top().s<in[i].s) s.pop();
		s.push(in[i]);
	}
	in.clear();
	while(!s.empty()){
		in.push_back(s.top());
		s.pop();
	}
}

void init(int id,int l,int r){//对每个块预处理，id为块编号
	for(int i=l;i<=r;i++){//暴力dp
		long long v=INF;
		for(int j=i;j<=r;j++){
			v=min(v+d[j],lim[j]);
			g[id][i-l][j-l]=v;
		}
	}
	vright[id].clear();
	for(int i=l;i<=r;i++){
		vright[id].push_back(val(get_g(l,i),get_s(l,i)));
	}
	del_small(vright[id]);
	vblock[id].clear();
	for(int i=l;i<=r;i++){
		for(int j=i;j<=r;j++){
			vblock[id].push_back(val(get_g(i,j),get_s(i,j)));
		}
	}
	del_small(vblock[id]);
	vleft[id].clear();
	for(int i=l;i<=r;i++){
		vleft[id].push_back(val(get_g(i,r),get_s(i,r)));
	}
	del_small(vleft[id]);

}

long long find_mpos(vector<val> &v,long long x0){
	//求之前的值x0，再加上v数组中的最大值之后的答案 
	//s单调递增，g单调递减,二分找到交点 
	int l=0,r=v.size()-1,mid,ans=0;
	while(l<=r){
		mid=(l+r)>>1;
		if(v[mid].g>=v[mid].s+x0){
			ans=mid;
			l=mid+1;
		}else r=mid-1;
	}
	long long res=0;
	//可能ans,ans+1在交点两侧，取max 
	if(ans+1<v.size()) //注意边界
       res=max(min(v[ans].g,v[ans].s+x0),min(v[ans+1].g,v[ans+1].s+x0));
	else res=min(v[ans].g,v[ans].s+x0);
	return res;
}

long long query(int l,int r,long long x0){//查询l,r,x0
	long long ans=x0,tmp;//tmp为从l到当前位置的答案 ,ans表示目前最优答案
	tmp=x0;
	for(int i=l;i<=min(rb(id[l]),r);i++){//不完整块的暴力
		tmp=min(max(tmp,x0)+d[i],lim[i]);
		ans=max(ans,tmp);
	}
	for(int i=id[l]+1;i<id[r];i++){
		ans=max(ans,find_mpos(vright[i],tmp));
        //find_mpos(v,x0)是按上述方法求v中最大值，且加上x0
        //从前面的块走过来，从本块结束，把tmp当成x0传进去，相当于把这块之前的答案也累计进去，再加上v里面的部分即是从前面到本块的答案
		ans=max(ans,find_mpos(vblock[i],x0));
        //从本块开始，从本块结束
		tmp=min(get_g(lb(i),rb(i)),get_s(lb(i),rb(i))+tmp);
        //从这一块前面开始走到这一块后面，不在本块结束，所以不更新ans,把本块的g值和s值累计入tmp
		tmp=max(tmp,find_mpos(vleft[i],x0));
        //从本块开始，走到块尾
        
        //从这一块前面开始走到这一块后面，不在本块结束这种情况的值已经存在tmp里了，等到了结束的地方再更新ans,这里不用写
	}
	if(id[l]!=id[r]){
		for(int i=lb(id[r]);i<=r;i++){//不完整块的暴力
			tmp=min(max(tmp,x0)+d[i],lim[i]);
			ans=max(ans,tmp);
		}
	}
	return ans;
}

int main(){
	int l,r;
	long long x0;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%lld",&d[i]); 
		sum[i]=sum[i-1]+d[i];
	}
	for(int i=1;i<=n;i++){
		scanf("%lld",&lim[i]); 
	}
	sz=sqrt(n);
	cnt=1;
	for(int i=1;i<=n;i++){
		id[i]=cnt;
		if(i%sz==0) cnt++;
	}
	for(int i=1;i<=cnt;i++){
		init(i,lb(i),rb(i));
	}
	for(int i=1;i<=m;i++){
		scanf("%d %d %lld",&l,&r,&x0);
		printf("%lld
",query(l,r,x0));
	}
}