[HNOI2016]树(可持久化线段树+树上倍增)
题面
给出一棵n个点的模板树和大树,根为1,初始的时候大树和模板树相同。接下来操作m次,每次从模板树里取出一棵子树,把它作为新树里节点y的儿子。操作完之后有q个询问,询问新树上两点之间的距离
(n,m,q leq 1 imes 10^5)
分析
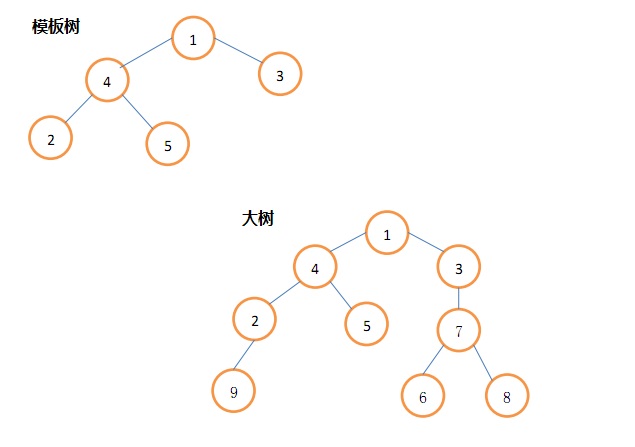
显然直接把所有节点存下来是不行的,因为节点的个数最多可以到(10^{10})。发现本质不同的子树只有n个,我们考虑把子树缩成一个点,构造一棵新树。
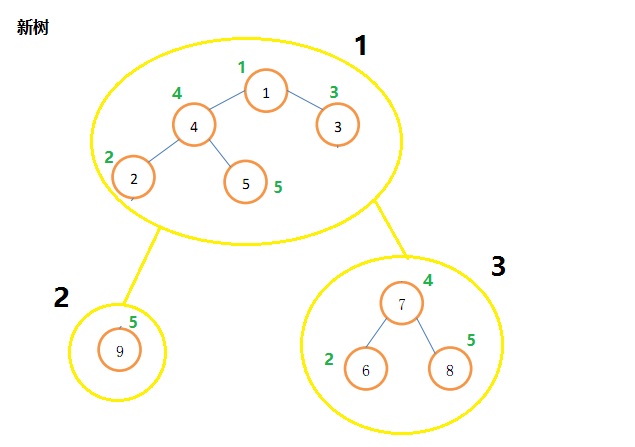
新树上的点有3种编号,注意区分:
1.小节点的询问编号,即图中淡黑色数字(1~9),询问和加点的时候被输入,可能会爆int
2.所在大节点编号,即图中加粗的黑色数字
3.在模板树上对应的点的编号,即图中绿色数字
定义两个大节点之间的边权为大节点对应子树的树根和被挂上的节点在模板树上的距离+1。每一个大节点需要存储:
1.子树内小节点询问编号的范围idl[x],idr[x]
2.根节点在模板树上对应的点的编号from[x]
3.这棵子树接到的节点的询问编号link[x]
然后写两个函数
1.get_root(x) 找到询问编号为x的节点所在大节点的编号。只需要二分答案,找到满足idl[k]<=x的最小k即可
2.get_tpid(x) 找到询问编号为x的节点在模板树上的编号。由于新加入大树的结点是按照在模板树中编号的顺序重新编号,那么他们的大小顺序不变。我们先找到x所在大节点rt,再找到rt在模板树上对应的点的编号from[rt],显然答案是from[rt]的子树中第x-idl[rt]+1小的节点编号。只需要在模板树上按照dfs序建出主席树,维护编号的出现情况即可。
然后在大节点构成的树上进行树上倍增,维护lca和x往上走2^i步的边权和。
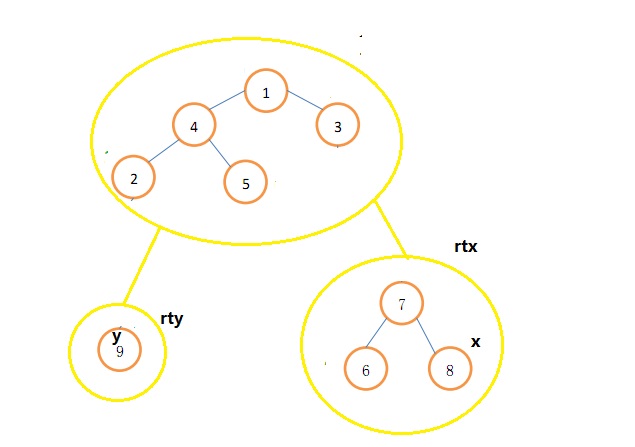
准备工作已经做完,我们来考虑如何求(x,y)距离
如图,我们先加上模板树上x到rtx的距离,然后在新树上像求lca一样往上跳,同时累计距离。直到x,y的父亲相同。
但是这里跳到最后一步的时候会出问题。如图,我们求9到5的距离,从rty直接跳到rty的父亲1会出问题,因为这样并不是最短路径,应该从rty跳到link[rty]才对,所以最后一步特判一下即可,x,y最后一步的距离为1+1+模板树上link[x]到link[y]的距离,其中1表示从a跳到link[a]的距离为1
本题细节很多,建议写完后先静态查错一遍,再对拍。本篇最末尾有数据生成器代码,欢迎使用。
代码
AC代码
//大毒瘤!!!!!!!
//
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define maxn 100000
#define maxlogn 20
using namespace std;
typedef long long ll;
int n,m,q;
struct persist_segment_tree{
#define lson(x) tree[x].ls
#define rson(x) tree[x].rs
struct node{
int ls;
int rs;
int cnt;
}tree[maxn*maxlogn+5];
int root[maxn+5];
int ptr;
void push_up(int x){
tree[x].cnt=tree[lson(x)].cnt+tree[rson(x)].cnt;
}
void update(int &x,int last,int upos,int l,int r){
x=++ptr;
tree[x]=tree[last];
if(l==r){
tree[x].cnt++;
return;
}
int mid=(l+r)>>1;
if(upos<=mid) update(tree[x].ls,tree[last].ls,upos,l,mid);
else update(tree[x].rs,tree[last].rs,upos,mid+1,r);
push_up(x);
}
int query(int xl,int xr,int k,int l,int r){
if(l==r) return l;
int mid=(l+r)>>1;
int cnt=tree[lson(xr)].cnt-tree[lson(xl)].cnt;
if(k<=cnt) return query(tree[xl].ls,tree[xr].ls,k,l,mid);
else return query(tree[xl].rs,tree[xr].rs,k-cnt,mid+1,r);
}
#undef lson
#undef rson
}CT;
namespace template_tree{
struct edge{
int from;
int to;
int next;
}E[maxn*2+5];
int esz=1;
int head[maxn+5];
void add_edge(int u,int v){
esz++;
E[esz].from=u;
E[esz].to=v;
E[esz].next=head[u];
head[u]=esz;
esz++;
E[esz].from=v;
E[esz].to=u;
E[esz].next=head[v];
head[v]=esz;
}
int log2n;
int anc[maxn+5][maxlogn+5];
int deep[maxn+5];
int tim;
int dfnl[maxn+5],dfnr[maxn+5];
int hash_dfn[maxn+5];
void dfs(int x,int fa){
deep[x]=deep[fa]+1;
dfnl[x]=++tim;
hash_dfn[tim]=x;
anc[x][0]=fa;
for(int i=1;i<=log2n;i++) anc[x][i]=anc[anc[x][i-1]][i-1];
for(int i=head[x];i;i=E[i].next){
int y=E[i].to;
if(y!=fa){
dfs(y,x);
}
}
dfnr[x]=tim;
}
int lca(int x,int y){
if(deep[x]<deep[y]) swap(x,y);
for(int i=log2n;i>=0;i--){
if(deep[anc[x][i]]>=deep[y]){
x=anc[x][i];
}
}
if(x==y) return x;
for(int i=log2n;i>=0;i--){
if(anc[x][i]!=anc[y][i]){
x=anc[x][i];
y=anc[y][i];
}
}
return anc[x][0];
}
int get_dist(int u,int v){
return deep[u]+deep[v]-2*deep[lca(u,v)];
}
int get_son_kth(int x,int k){//查询子树中第k大
return CT.query(CT.root[dfnl[x]-1],CT.root[dfnr[x]],k,1,n);
}
void build(){
log2n=log2(n)+1;
dfs(1,0);
for(int i=1;i<=n;i++) CT.update(CT.root[i],CT.root[i-1],hash_dfn[i],1,n);
}
}
namespace real_tree{
struct edge{
int from;
int to;
int len;
int next;
}E[maxn*2+5];
int esz=1;
int head[maxn+5];
void add_edge(int u,int v,int w){
esz++;
E[esz].from=u;
E[esz].to=v;
E[esz].next=head[u];
E[esz].len=w;
head[u]=esz;
esz++;
E[esz].from=v;
E[esz].to=u;
E[esz].next=head[v];
E[esz].len=w;
head[v]=esz;
}
int log2n;
int deep[maxn+5];
ll dist[maxn+5];
int anc[maxn+5][maxlogn+5];
ll dsum[maxn+5][maxlogn+5];//x向上走2^i辈祖先的距离
void dfs(int x,int fa){
deep[x]=deep[fa]+1;
anc[x][0]=fa;
for(int i=1;i<=log2n;i++){
anc[x][i]=anc[anc[x][i-1]][i-1];
dsum[x][i]=dsum[x][i-1]+dsum[anc[x][i-1]][i-1];
}
for(int i=head[x];i;i=E[i].next){
int y=E[i].to;
if(y!=fa){
dist[y]=dist[x]+E[i].len;
dsum[y][0]=E[i].len;
dfs(y,x);
}
}
}
struct oper{
int x;
ll to;
}op[maxn+5];
ll idl[maxn+5],idr[maxn+5];//这个大节点包含小节点的编号范围
int from[maxn+5];//大节点来自模板树上的节点编号
ll link[maxn+5];//记录一下大节点x接到了哪里
int sz;
int get_root(ll x){//找到包含小节点的大节点
//二分出包含小节点的区间
int l=1,r=sz;
int mid;
int ans=0;
while(l<=r){
mid=(l+r)>>1;
if(idr[mid]>=x){
ans=mid;
r=mid-1;
}else l=mid+1;
}
return ans;
}
int get_tpid(ll x){//找到小节点x在模板树里对应的节点
//实际上就是找模板树子树from[rt]里第x-idl[rt]+1小的节点,用主席树做
int rt=get_root(x);
return template_tree::get_son_kth(from[rt],x-idl[rt]+1);
}
void build(){
sz=1;
ll cnt=n;
from[1]=1;
idl[1]=1;
idr[1]=n;
for(int i=1;i<=m;i++){
sz++;
int rt=get_root(op[i].to);
int len=template_tree::get_dist(from[rt],get_tpid(op[i].to))+1;
add_edge(sz,rt,len);
link[sz]=op[i].to;
from[sz]=op[i].x;
idl[sz]=cnt+1;
idr[sz]=cnt+template_tree::dfnr[op[i].x]-template_tree::dfnl[op[i].x]+1;
cnt=idr[sz];
}
log2n=log2(sz)+1;
dfs(1,0);
}
ll get_dist(ll x,ll y){
int rtx=get_root(x);
int rty=get_root(y);
ll ans=0;
if(rtx==rty){
return template_tree::get_dist(get_tpid(x),get_tpid(y));
}else{
if(deep[rtx]<deep[rty]){
swap(x,y);
swap(rtx,rty);
}
ans+=template_tree::get_dist(get_tpid(x),from[rtx]);//x到rtx的距离
x=rtx;
for(int i=log2n;i>=0;i--){
if(deep[anc[x][i]]>deep[rty]){//差一步不要跳
ans+=dsum[x][i];
x=anc[x][i];
}
}
if(anc[x][0]==rty) return ans+1+template_tree::get_dist(get_tpid(link[x]),get_tpid(y));
//如果是一条链,需要特判,这里不能在大树上跳一步到rty,因为经过rty不是最短路径,
//如果x到rty有一条边,即x对应的子树的根是接在rty中的某个小节点的子树上的
//应从x对应子树的根,跳长度为1到link[x],再从link[x]到y
ans+=template_tree::get_dist(get_tpid(y),from[rty]);//y到rty的距离
y=rty;
if(deep[x]>deep[rty]){
ans+=dsum[x][0];
x=anc[x][0];
}//如果不是一条链,且深度不等,才跳到同一深度
for(int i=log2n;i>=0;i--){
if(anc[x][i]!=anc[y][i]){
ans+=dsum[x][i];
ans+=dsum[y][i];
x=anc[x][i];
y=anc[y][i];
}
}
//最后一步
x=link[x];
y=link[y];
ans+=2;
ans+=template_tree::get_dist(get_tpid(x),get_tpid(y));
return ans;
}
}
}
int main(){
int u,v;
ll xx,yy;
scanf("%d %d %d",&n,&m,&q);
for(int i=1;i<n;i++){
scanf("%d %d",&u,&v);
template_tree::add_edge(u,v);
}
template_tree::build();
for(int i=1;i<=m;i++){
scanf("%d %lld",&real_tree::op[i].x,&real_tree::op[i].to);
}
real_tree::build();
for(int i=1;i<=q;i++){
scanf("%lld %lld",&xx,&yy);
printf("%lld
",real_tree::get_dist(xx,yy));
}
}
数据生成器
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
#define maxn 5
#define maxm 3
#define maxq 5
#define maxv 1000
using namespace std;
typedef long long ll;
ll random(ll n){
return (ll)rand()*rand()%n+1;
}
ll random(ll l,ll r){
return (ll)rand()*rand()%(r-l+1)+l;
}
int n,m,q;
struct edge{
int from;
int to;
int next;
}E[maxn*2+5];
int esz=1;
int head[maxn+5];
void add_edge(int u,int v){
esz++;
E[esz].from=u;
E[esz].to=v;
E[esz].next=head[u];
head[u]=esz;
}
int sz[maxn+5];
void dfs(int x,int fa){
sz[x]=1;
for(int i=head[x];i;i=E[i].next){
int y=E[i].to;
if(y!=fa){
dfs(y,x);
sz[x]+=sz[y];
}
}
}
ll newn;
int main(){
srand(time(NULL));
n=random(2,maxn);
m=random(maxm);
q=random(maxq);
printf("%d %d %d
",n,m,q);
for(int i=2;i<=n;i++){
int u=random(i-1);
add_edge(u,i);
add_edge(i,u);
printf("%d %d
",i,u);
}
dfs(1,0);
newn=n;
for(int i=1;i<=m;i++){
int x=random(n);
printf("%d %lld
",x,random(newn));
newn+=sz[x];
}
for(int i=1;i<=q;i++){
printf("%lld %lld
",random(newn),random(newn));
}
}