1. 原始优化问题等价拉格朗日的极小极大问题
原始优化问题
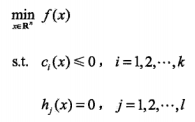
为不等式约束
为等式约束
广义拉格朗日函数
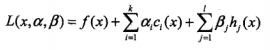
其中称为拉格朗日乘子,
考虑以下关于x的函数:
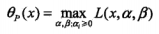
有:

则的极小化问题就等价于原优化问题:
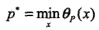
则称为广义拉格朗日函数的极小极大问题
2. 对偶问题
原始问题的对偶问题为广义拉格朗日函数的极大极小问题,即:
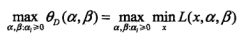
3. 原问题和对偶问题的关系
定理1
原优化问题与对偶问题最优值的关系:
定理2
当原优化问题为凸优化问题,且满足slater条件时则存在使得:
即对原优化问题的求解可以转化为对对偶问题的求解。
凸优化问题满足两个条件:
- 可行域为凸集;(可行域中任意两点之间的连线人在该可行域中)
- 函数为凸函数
slater条件是指,凸集的交集有内点。(凸集的交集仍为凸集,但不一定有内点)
定理3
满足KKT条件,则为原问题和对偶问题的解。(前提是满足定理2成立的条件)