一、开发时间
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 5 | 6 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 420 | 840 |
| · Design Spec | · 生成设计文档 | 120 | 180 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 20 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 20 | 30 |
| · Coding | · 具体编码 | 120 | 360 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 120 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 20 | 20 |
| · Size Measurement | · 计算工作量 | 20 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 20 |
| 合计 | 855 | 1656 |
二、解题思路描述
显然-c与-s要通过不同的方法去实现,毕竟一个是生成数独,另一个是解数独,看起来是两种不同的操作。
1)关于数独的生成(-c)
网上的做法多种多样,其中思路较为简单的是回溯法。但在我看来,回溯的方法总是效率低下的,所以我采用了用一个种子(即9X9宫格的部分)去生成整个数独终局的办法,只要保证种子的随机性与不重复性,即可保证整个数独终局的随机性与不重复性。
对于9X9的数独,取左上角3X3的宫格进行分析。由于我的学号末尾是49,则最左上角的宫格为(4+9)%9+1=5,则剩下的宫格有8!=40320种排列,与要求的1000000个不同数独还差两个0的数量级。这时候把目光转向第二个3X3的宫格,则第一行填法有A(6,3)种,而A(6,3)=120正好为两个0的数量级。这样一来,只要确保第一个3X3宫格与第二个3X3宫格第一行(即图中的ABC)的唯一性,通过如图交换行列的做法,就可以生成1000000个不同的数独。
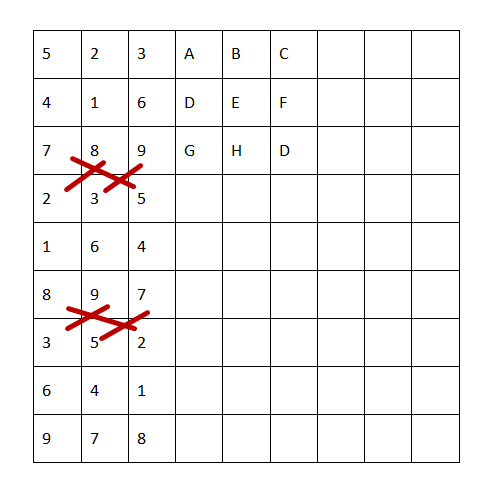
2)关于数独的解决(-s)
在网上以及和宿舍同学学习了一圈,找到一种业内公认最快的方法叫DXL(舞蹈链)的做法。尽管还是用到了我不太喜欢的dfs,但起码这个dfs是有界的,就在一个链表中递归。算法的具体说明在舍友推荐的这篇博客里已经说得清楚明白http://www.cnblogs.com/grenet/p/3163550.html。我本人对于一些细节的实现还一知半解,但会用就行。
把解数独转化为精确覆盖问题关键在于怎么生成双向链表。对于链表的行来说,一共9X9个小格,每个小格有9种填法,则可生成9X9X9=729行;对于列,有(9+9+9)X9+81=324列,前面三个9代表数独宫格中的9行9列9小块,乘九意思是九种可能,81代表9X9共81个格子中每格只能放一个数字。读入数据后,如果为0,则表示可放9种数字,建9行,否则只能放一个已知数字,建一行。
生成了双向链表,就可以用dfs愉快地解题了!
三、设计实现
在主函数main中,包含以下三个类:
1)输入处理类:根据参数调用下列2)、3)函数进行相应处理(包括参数合法性判断)。
合法性判断包括:参数是否合法,是否输入非法字符,输入数字是否越界。
2)终盘生成类:终盘生成函数(generator)、排列组合函数(PailieZuhe)、查重函数(CheckRepete)、输出函数(Display),调用关系如图。
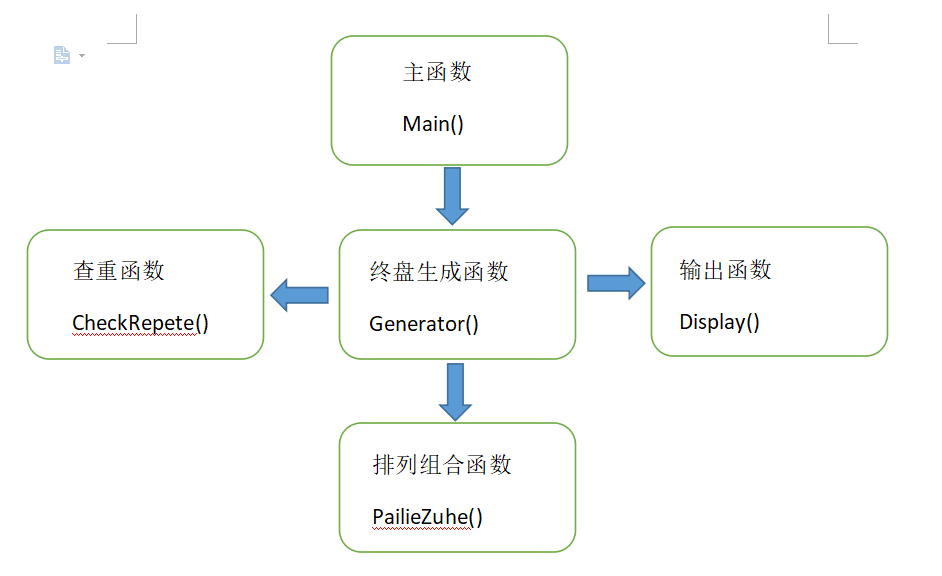
3)数独求解类:链接构建函数(Makecolhead)、结点插入函数(Add)、移除函数(Remove)、恢复函数(Resume)、深度优先遍历函数(Dfs),核心的Dfs函数流程图如下:
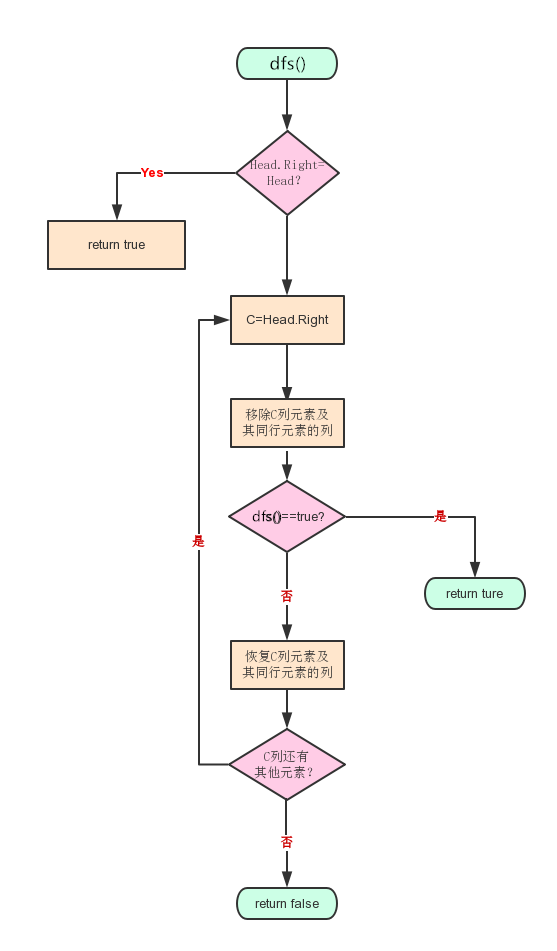
四、优化改进
1、对于“-c”操作,由于生成种子法的先天优势,在Release x64模式下生成1000000数独仅需要22s。根据性能分析器显示,主要的时间开销集中在一个叫[ucrtbase.dll]的块中。点开详细一看,调用[ucrtbase.dll]最多的函数是printf()输出函数。
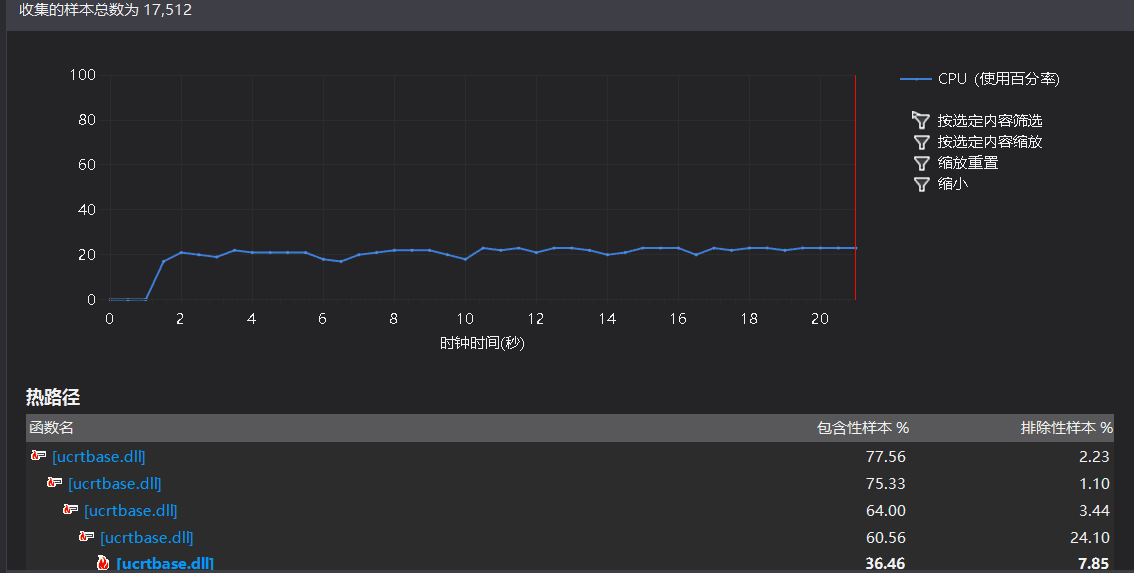
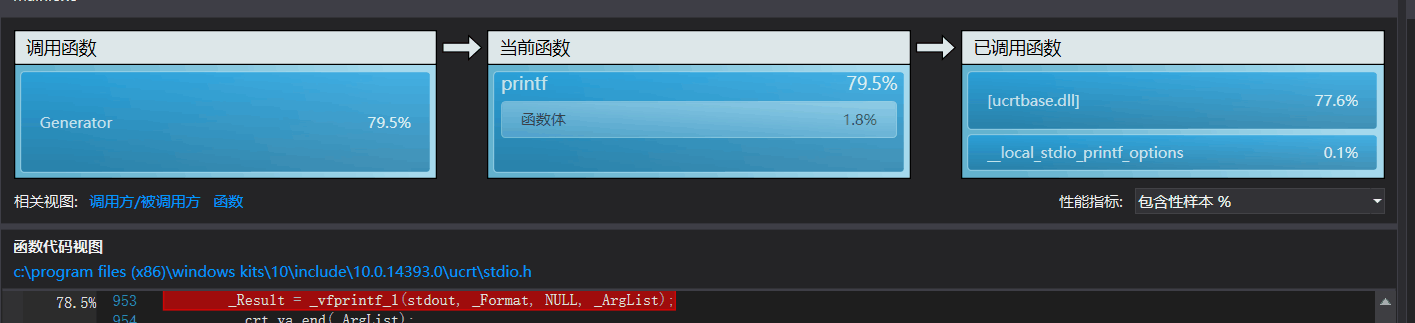
根据网上的资料显示,用put类型字符串输出的效率比printf()效率要高,于是将输出终局改为用puts()以字符串形式输出,效率果然大大提高。整个程序的花销主要变为是main函数与Generator模块这两个整体,而不是某一个局部,我认为继续优化的空间不大了。
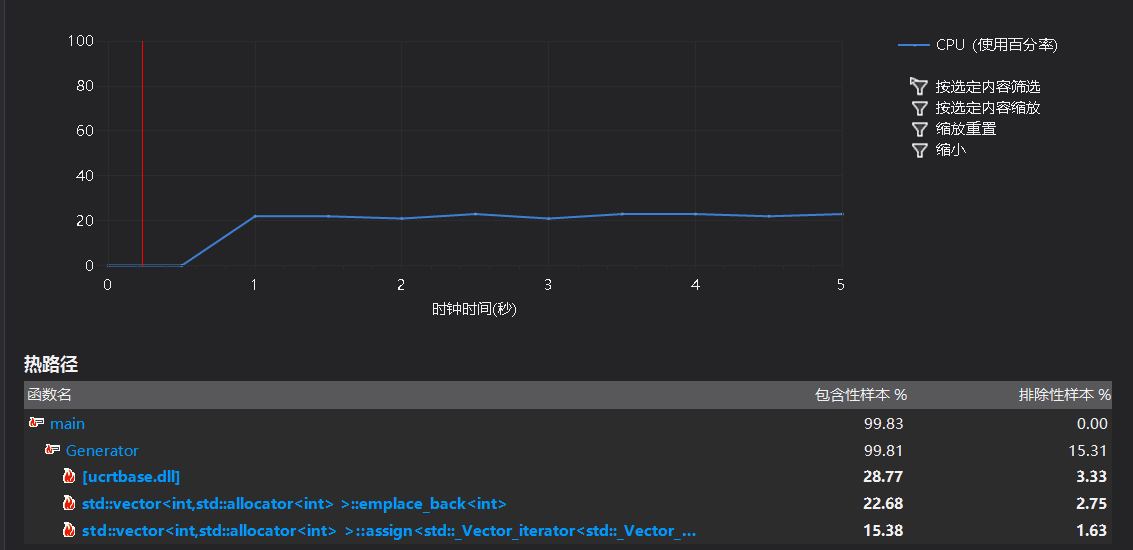
优化前后生成1000000w数独终局的时间对比如下:
| 模式 | 优化前 | 优化后 |
| Release x64 | 22.21s | 5.995s |
同理,对于“-s”操作,输入采用getchar(),输出采用puts(),时间也有了十几秒左右的提高。
2、对于"-s"操作,起初改写了网上的一版我看得懂的所谓大神DLX模板,解1000000个数独竟用了10m29s之久,这效率实在是太低下了。根据程序性能分析器显示,时间开销最大的是在建立双向列表的函数build()内一个双重的729*324的for循环(下图中的黄色框框内)。
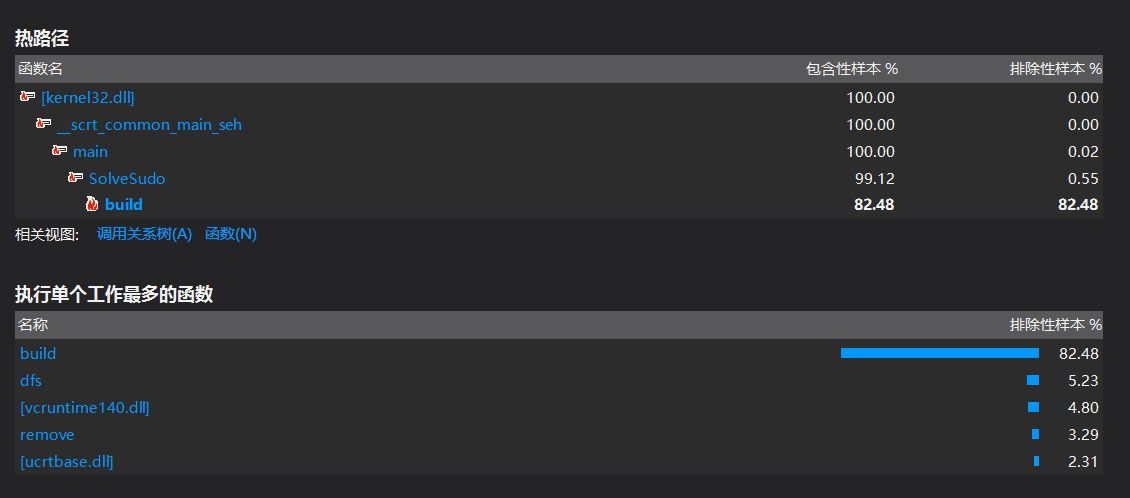
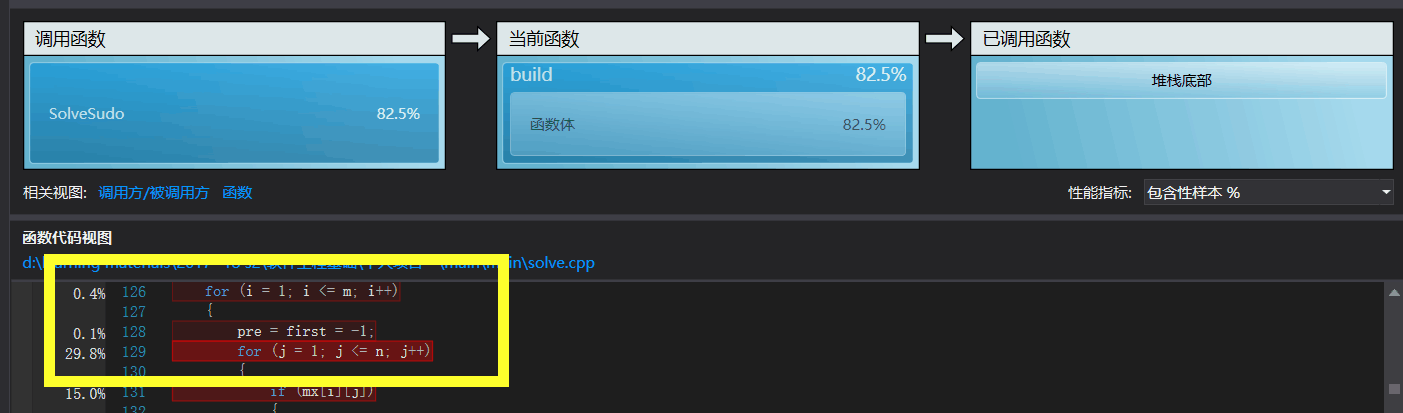
这可使我犯了难,建立双向列表是一个固有操作,应该怎么更改?想了许久没有头绪。好在同宿舍的大神舍友也用DXL法,而他的程序解1000000的数独仅用不到一分钟。他的程序我看不太懂,但是方法思路基本掌握了,在生成行和列的同时就构建双向链表,这样就不用等到生成完了所有行和列,再用双重for循环逐个排查来构建双向列表。但先前的版本毕竟是仿别人的模板,我也不好修改,只能重写一份,当做借鉴的教训吧。如此一来,效率的确大大提高,时间的主要开销转移到了dfs函数。可鉴于目前我的水平,剪枝并不是我的强项,我优化的努力只能到此为止了。
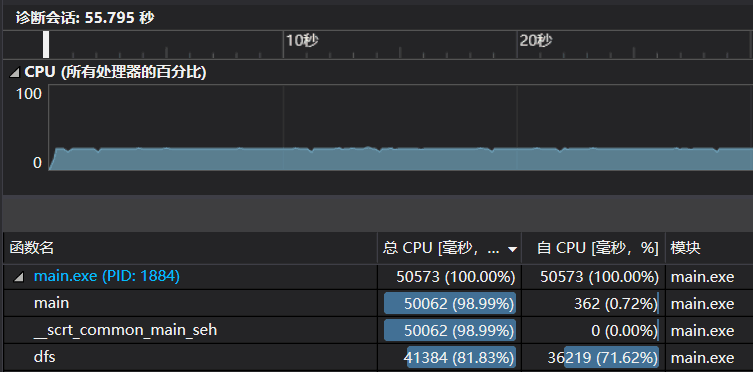
优化前后解1000000数独的时间对比如下:
| 模式 | 优化前 | 优化后 |
| Release x64 | 10m29s | 55.795s |
五、关键代码展示
1)输入参数的判断:分参数异常,出现非法字符,溢出等情况。
/*输入检验*/ if (strcmp(argv[1], "-c") == 0)//生成数独终局 { int N = 0; for (int i = 0; i < strlen(argv[2]); i++) { if (argv[2][i] < 48 || argv[2][i] > 57) { printf("Wrong Input! ");//非法输入(错误字符) return -1; } else { N = N + (argv[2][i] - '0') * pow(10, (strlen(argv[2]) - i - 1)); if (N < 0 || N>1000000) { printf("Overflow! ");//非法输入(越界) return -2; } } } int sudo[9][9]; Generator(N, sudo); } else if (strcmp(argv[1], "-s") == 0)//解数独 { } else if (strcmp(argv[1], "-c") != 0 && strcmp(argv[1], "-s") != 0)//错误参数 { printf("Wrong Input! "); return -3; }
2)"-c"生成随机不重复数独终局的generator部分的主要代码,思路为:
先使用随机的排列组合生成一个3X3的种子宫,使用查重函数判断,如果不重复,则继续。
用全排列生成第二个3X3种子宫A(6,3)=120个不同的排列,逐一与第一个3X3种子宫匹配,交换行列生成数独终局输出,当用完这120个排列时,回到随机生成3X3种子宫一步。
using namespace std; extern vector<vector<int>> arrange; void Get_Seedbox(vector<int> &Seed_Box)//随机生成开头为5的3x3种子宫 { Seed_Box = Pailie_Zuhe_Random(Seed_Box); for (int i = 0; i < 9; i++) { if (Seed_Box[i] == 5) { swap(Seed_Box[i], Seed_Box[0]); break; } } } void Set_Sudo(int(*sudo)[9], const vector<int> &Seed_Box, int count)//初始化函数 { for (int i = 0; i < 9; i++) for (int j = 0; j < 9; j++) sudo[i][j] = 0; for (int i = 0, k = 0; i < 3; i++) for (int j = 0; j < 3; j++) sudo[i][j] = Seed_Box[k++]; sudo[0][3] = arrange[count][0]; sudo[0][4] = arrange[count][1]; sudo[0][5] = arrange[count][2]; } void Generator(int N, int(*sudo)[9]) { vector<int> Seed_Box; vector<int> Tmp_Box; for (int i = 0; i < 9; i++) Seed_Box.push_back(i + 1); while (N != 0) { Get_Seedbox(Seed_Box); if (!Check_Rep(Seed_Box))//检验重复性 continue; Tmp_Box.assign(Seed_Box.begin() + 3, Seed_Box.end());//获取第一宫第一行前三个外的6个数字,生成所有唯一的A(6,3) Pailie_Zuhe_All(Tmp_Box); int count = 0; while (N != 0) { if (count < 120) Set_Sudo(sudo, Seed_Box, count++); else break; for (int i = 1; i < 3; i++)//生成第二宫的第二行和第三行 { Tmp_Box.assign(Seed_Box.begin(), Seed_Box.end());//删除同行在第一宫的三个数 Tmp_Box.erase(Tmp_Box.begin() + i * 3); Tmp_Box.erase(Tmp_Box.begin() + i * 3); Tmp_Box.erase(Tmp_Box.begin() + i * 3); for (int j = 0; j < Tmp_Box.size(); j++)//删除已排序的数 if (Tmp_Box[j] == sudo[0][3] || Tmp_Box[j] == sudo[0][4] || Tmp_Box[j] == sudo[0][5] || Tmp_Box[j] == sudo[1][3] || Tmp_Box[j] == sudo[1][4] || Tmp_Box[j] == sudo[1][5]) Tmp_Box.erase(Tmp_Box.begin() + (j--)); /*第二行时只删了三个,多删三个*/ if (Tmp_Box.size() == 6) Tmp_Box.erase(Tmp_Box.begin()); if (Tmp_Box.size() == 5) Tmp_Box.erase(Tmp_Box.begin()); if (Tmp_Box.size() == 4) Tmp_Box.erase(Tmp_Box.begin()); Tmp_Box = Pailie_Zuhe_Random(Tmp_Box, Tmp_Box.size(), 3);//由于A(6,3)的唯一性,第二宫剩下的行任意生成一种排法即可 sudo[i][3] = Tmp_Box[0]; sudo[i][4] = Tmp_Box[1]; sudo[i][5] = Tmp_Box[2]; } for (int i = 0; i < 3; i++)//生成第三宫 { Tmp_Box.assign(Seed_Box.begin(), Seed_Box.end()); for (int j = 0; j < Tmp_Box.size(); j++)//删除第一二宫同行的数 if (Tmp_Box[j] == sudo[i][0] || Tmp_Box[j] == sudo[i][1] || Tmp_Box[j] == sudo[i][2] || Tmp_Box[j] == sudo[i][3] || Tmp_Box[j] == sudo[i][4] || Tmp_Box[j] == sudo[i][5]) Tmp_Box.erase(Tmp_Box.begin() + (j--)); Tmp_Box = Pailie_Zuhe_Random(Tmp_Box, 3, 3);//由于A(6,3)的唯一性,第二宫剩下的行任意生成一种排法即可 sudo[i][6] = Tmp_Box[0]; sudo[i][7] = Tmp_Box[1]; sudo[i][8] = Tmp_Box[2]; } for (int i = 3; i < 9; i++)//余下所有宫格由种子宫交替生成 { for (int j = 0; j < 9; j++) { if (j == 2 || j == 5 || j == 8) sudo[i][j] = sudo[i - 3][j - 2]; else sudo[i][j] = sudo[i - 3][j + 1]; } } display(sudo);//输出终局 N--; } } }
3)"-s"操作的关键代码,通过dfs对双向链表进行操作求得数独终局的代码如下:
bool dfs(const int& k)//深搜求解 { if (right[head] == head)//已经选够 { char s[100] = { 0 }; char output[20]; for (int i = 0; i<k; i++) s[ans[st[i]].r * 9 + ans[st[i]].c] = ans[st[i]].k + '0';//s[行*9+列] int count = 0; for (int i = 0; i < 9; i++) { int num = 0; output[num++] = s[count++]; for (int j = 1; j < 9; j++) { output[num++] = ' '; output[num++] = s[count++]; } output[num] = '�'; puts(output); } printf(" "); return true; } //遍历列标元素,选一个元素最少的列(回溯率低) int s = oo, c = 0; for (int i = right[head]; i != head; i = right[i]) if (cnt[i]<s) { s = cnt[i]; c = i; } remove(c);//选好就移除 //遍历该列各“1”元素 for (int i = down[c]; i != c; i = down[i]) { st[k] = row[i]; for (int j = right[i]; j != i; j = right[j]) // 移除与该元素同行元素的列 remove(col[j]); if (dfs(k + 1))// 已选行数+1,递归调用 return true; for (int j = left[i]; j != i; j = left[j])// 递归返回false,说明后续无法满足,故恢复与该元素同行元素的列,循坏进入本列下一元素 resume(col[j]); } resume(c);//所有后续都无法满足,恢复 return false; }
六、测试
由于单元测试用软件实现的编程实在是超出我能力范围,我只能采用手动设计测试用例的方法去进行测试。
1)对于“-c”
由于种子宫这一方法的先天优势,如果算法编写正确,不可能存在重复的情况,重复性可以不作检验。
对于输入,设计了1)非法参数 “-a 100” 2)非法字符 "-c abc"3)越界"-c 9999999" 三种测试用例,均输出了输入异常的判断。
2)对于"-s"
将"-c"的部分输出改为0,即可设计出最多1000000个数独题目的用例。
此外还设计了一些无解的数独或格式不对(3X3宫格内有重复数字)的数独进行测试,均输出回车表示无解。
看起来这测试结果令人满意,希望可以通过老师的正确性测试。
心得体会
做完了个人项目,可以说是筋疲力尽。因为要较好的完成这个项目,做出一个高效的程序,自己需要自学的东西是在是太多太多了(最后完成的实际时间比预计翻了一番),对平时只关心课堂教学内容,自学动手能力不高,又想全力完成好这个项目的我,真是一个巨大的挑战。即使我在小学期有充分的时间做这个项目,我都会感觉掉一层皮,更何况在正规的学期内从这么多科目中抽出大量时间去完成这一个项目,掉了简直是N层皮。在开始的要求中,能用的C++,C#我真是一个都没学过,便盼着老师更改题目,可好歹加了C语言吧,经过一番学习调查,发现用C语言较好完成这个项目的难度,不亚于速成C++然后用它来实现这个项目。最后用将近一个月的时间加上汗水和泪水,完成了这个对我来说是巨大挑战的项目。
总而言之,经过这次项目的实践,我精神属性上的提高,要大于技术属性上的提高。一开始面对着别班上着水水的课,自己却要做这么难一个项目的情形,心里是十分十分十分抵触的。但自从老师在课上对自己的教学方法与教学目的做了一场慷慨激昂的演讲,我的脑海里浮现出这个项目时,竟多了老师一张挂着鼓励微笑的脸。面对这个项目,我再怎么感叹自己水平不足,再怎么烦恼毫无头绪,一想起老师的鼓励和笑容,我就又有了坚持下去的动力。如今惨痛的一个月过去了,写下这项目的总结,真有一种说不出来的感慨万千。尽管限于能力和时间有些要求比如单元测试和GUI,我尽最大努力也没法按时交出一个较好的作品;还有些部分因为自学的不系统不深入浅尝辄止酿成大祸,比如以为commit之后还可以改,酿成了commit都是“update+文件名”的惨案。但日后的实际工作中编写项目不也是一样吗?尽善尽美是可遇而不可求的,但为此认真努力付出过,也没什么好后悔了。
最后感谢老师,让还在大二,几乎还是一张白纸的我超前体验了一把自学做项目的快感。