CSharpGL(53)漫反射辐照度
本系列将通过翻译(https://learnopengl.com)这个网站上关于PBR的内容来学习PBR(Physically Based Rendering)。
本系列共4篇。由于前2篇已经有人翻译过了(https://learnopengl-cn.github.io/07%20PBR/01%20Theory/),我暂时就跳过,直接翻译第3篇。
本篇讲了什么,我也不太懂。不过我在CSharpGL中已经实现了一个PBR的demo。代码都有了,早晚会懂的。
下载
CSharpGL已在GitHub开源,欢迎对OpenGL有兴趣的同学加入(https://github.com/bitzhuwei/CSharpGL)
正文
Diffuse irradiance漫反射辐照度
IBL or image based lighting is a collection of techniques to light objects, not by direct analytical lights as in the previous tutorial, but by treating the surrounding environment as one big light source.
IBL(Image Based Lighting)是一些特别的光照技术,它们不像之前的教程那样,用直接光源(点光源、平行光、聚光灯之类)照射物体,而是将物体周围的整个环境当作一个大大的光源。
This is generally accomplished by manipulating a cubemap environment map (taken from the real world or generated from a 3D scene) such that we can directly use it in our lighting equations: treating each cubemap pixel as a light emitter.
这通常是用一个cubemap来实现的,这个cubemap可能来自真实世界,或者是用3D场景生成的。我们就可以直接把它加入光照方程:将cubemap的每个像素都当作一个发光点。
This way we can effectively capture an environment's global lighting and general feel, giving objects a better sense of belonging in their environment.
这样我们就可以有效地捕捉到环境带来的全局光照和大致感觉,让人更能感到这个物体属于它所在的环境。
As image based lighting algorithms capture the lighting of some (global) environment its input is considered a more precise form of ambient lighting, even a crude approximation of global illumination.
由于IBL算法捕捉了某种全局环境的光照,它的输入被认为是一种更加精确的环境光,甚至是一种简陋的全局照明。
This makes IBL interesting for PBR as objects look significantly more physically accurate when we take the environment's lighting into account.
当我们将环境光照考虑进来后,物体会达到物理精确的视觉效果。这是IBL在PBR中最有趣的地方。
To start introducing IBL into our PBR system let's again take a quick look at the reflectance equation:
介绍IBL之前,我们先来回顾一下反射率方程:
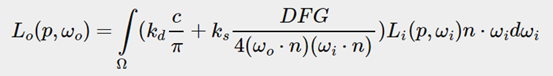
As described before, our main goal is to solve the integral of all incoming light directions wi over the hemisphere Ω.
如前所述,我们的主要目标是求解所有的入射光方向wi在半球Ω上的积分。
Solving the integral in the previous tutorial was easy as we knew beforehand the exact few light directions wiwi that contributed to the integral.
在之前的教程中求解这个积分很容易,因为我们知道有哪个光线wi对积分有贡献。
This time however, every incoming light direction wi from the surrounding environment could potentially have some radiance making it less trivial to solve the integral.
然而这次呢,从周围环境来的每个入射光线都可能照射到物体上。我们无法绕过求解积分的过程了。
This gives us two main requirements for solving the integral:
这对我们求解积分提出了2项要求:
l We need some way to retrieve the scene's radiance given any direction vector wi.
我们需要某种方法能够找到场景在任何方向wi上的辐射率。
l Solving the integral needs to be fast and real-time.
求解积分的过程必须是快速实时的。
Now, the first requirement is relatively easy.
好吧,第一个要求相对简单。
We've already hinted it, but one way of representing an environment or scene's irradiance is in the form of a (processed) environment cubemap.
我们提示过,一种表示环境或场景的辐照度的形式是用环境cubemap。
Given such a cubemap, we can visualize every texel of the cubemap as one single emitting light source.
给定这样一个cubemap,我们可以将它的每个纹素(texel)视为一个独立的光源。
By sampling this cubemap with any direction vector wi we retrieve the scene's radiance from that direction.
从任意一个方向wi上对此cubemap采样,都可以得到此方向上的辐射度。
Getting the scene's radiance given any direction vector wi is then as simple as:
获取场景在某个方向上的辐射度就简单地表示如下了:
vec3 radiance = texture(_cubemapEnvironment, w_i).rgb;
Still, solving the integral requires us to sample the environment map from not just one direction, but all possible directions wi over the hemisphere Ω which is far too expensive for each fragment shader invocation.
可惜,求积分就要求我们不止对一个方向wi进行计算,而是要对所有可能的方向在半球Ω上进行累加。这对Fragment Shader来说承受不起。
To solve the integral in a more efficient fashion we'll want to pre-process or pre-compute most of its computations.
为了更高效地求解积分,我们要做一些预计算。
For this we'll have to delve a bit deeper into the reflectance equation:
为此我们要要更深入地研究一下反射率方程:
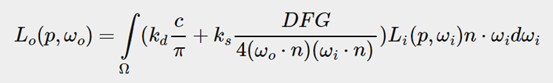
Taking a good look at the reflectance equation we find that the diffuse kd and specular ks term of the BRDF are independent from each other and we can split the integral in two:
仔细观察反射率方程我们发现BRDF的diffuse部分kd和specular部分ks是相互独立的,我们可以将积分拆分为2部分:

By splitting the integral in two parts we can focus on both the diffuse and specular term individually; the focus of this tutorial being on the diffuse integral.
拆分之后我们可以分别关注diffuse和specular部分。本教程关注diffuse部分。
Taking a closer look at the diffuse integral we find that the diffuse lambert term is a constant term (the color c, the refraction ratio kd and π are constant over the integral) and not dependent on any of the integral variables.
仔细观察diffuse部分,我们发现diffuse的lambert部分是个常量(颜色c,折射率kd和π都是常量),不依赖于积分中的变量。
Given this, we can move the constant term out of the diffuse integral:
基于此,我们可以把常量部分移出diffuse积分:
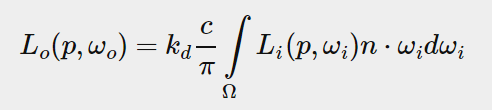
This gives us an integral that only depends on wi (assuming p is at the center of the environment map).
这样,积分部分就只有wi一个变量了(假设p在环境贴图的中心)。
With this knowledge, we can calculate or pre-compute a new cubemap that stores in each sample direction (or texel) wo the diffuse integral's result by convolution.
知道了这点,我们就可以预先计算出一个cubemap,让它保存每个方向上关于wo的diffuse积分值。计算方式是卷积。
Convolution is applying some computation to each entry in a data set considering all other entries in the data set; the data set being the scene's radiance or environment map.
如果说数据集是场景中的辐射率或者环境贴图,那么卷积就是对数据集中任意两部分的某种计算(这句我不会,瞎扯的)
Thus for every sample direction in the cubemap, we take all other sample directions over the hemisphere Ω into account.
因此,对于cubemap上的每个采样的方向,我们取半球Ω上所有其他采样方向参与计算。
To convolute an environment map we solve the integral for each output wo sample direction by discretely sampling a large number of directions wi over the hemisphere Ω and averaging their radiance.
在半球Ω上,离散地在大量方向上采样,求辐射率的均值。对每个方向都执行这样的操作,就可以实现对环境贴图的卷积。(瞎扯的)
The hemisphere we build the sample directions wi from is oriented towards the output wo sample direction we're convoluting.
我们在其上采样的半球,朝向输出wo。
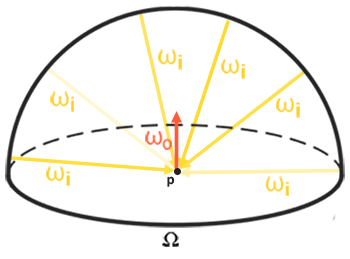
This pre-computed cubemap, that for each sample direction wo stores the integral result, can be thought of as the pre-computed sum of all indirect diffuse light of the scene hitting some surface aligned along direction wo.
这个预计算的cubemap,存储着与每个采样方向wo对映的积分结果。这个结果,就是场景光源照射到一个表面上(并且从wo方向观察)此表面时的diffuse值。
Such a cubemap is known as an irradiance map seeing as the convoluted cubemap effectively allows us to directly sample the scene's (pre-computed) irradiance from any direction wo.
这样的cubemap被称为辐照度贴图,它允许我们直接通过采样获得从任意方向wo观察场景时间接光源带来的辐照度。
The radiance equation also depends on a position p, which we've assumed to be at the center of the irradiance map.
辐射率方程还依赖一个位置变量p,我们已经假设它在辐照度贴图的中心了。
This does mean all diffuse indirect light must come from a single environment map which may break the illusion of reality (especially indoors).
这确实意味着所有的间接光源带来的diffuse部分都只能来自这一个环境贴图。这可能会打破真实感(特别是在室内)。
Render engines solve this by placing reflection probes all over the scene where each reflection probes calculates its own irradiance map of its surroundings.
渲染引擎通过在各个位置放置反射探针来解决这个问题。每个反射探针各自计算它周围的辐照度贴图。
This way, the irradiance (and radiance) at position p is the interpolated irradiance between its closest reflection probes.
如此一来,在位置p处的辐照度(和辐射度)就通过最近的几个反射探针进行插值得到。
For now, we assume we always sample the environment map from its center and discuss reflection probes in a later tutorial.
我们暂时假设我们总是在环境贴图的中心采样,在以后教程中再讨论反射探针。
Below is an example of a cubemap environment map and its resulting irradiance map (courtesy of wave engine), averaging the scene's radiance for every direction wo.
下图是一个cubemap环境贴图及其辐照度贴图(经由wave engine提供),它对场景中的每个方向wo都记录了辐射度。

By storing the convoluted result in each cubemap texel (in the direction of wo) the irradiance map displays somewhat like an average color or lighting display of the environment.
辐照度贴图存储着每个cubemap纹素(在wo方向上)的卷积结果,这使得它看起来像是平均化的颜色值。
Sampling any direction from this environment map will give us the scene's irradiance from that particular direction.
从这个环境贴图中的任何方向上采样都会给我们从那个方向上观察得到的场景的辐照度。
PBR and HDR
PBR:Physically Based Rendering. HDR: High Dynamic Range.
We've briefly touched upon it in the lighting tutorial: taking the high dynamic range of your scene's lighting into account in a PBR pipeline is incredibly important.
我们在光照教程中曾简要地提及:在PBR算法中加入HDR技术是极其重要的。
As PBR bases most of its inputs on real physical properties and measurements it makes sense to closely match the incoming light values to their physical equivalents.
PBR算法的大部分输入都是基于物理属性的,最合理的做法就是让输入光源的数值与它们的物理量相匹配。
Whether we make educative guesses on each light's radiant flux or use their direct physical equivalent, the difference between a simple light bulb or the sun is significant either way.
无论我们对光源的辐射通量值使用合理的猜测还是直接使用它们的物理值,一个普通的灯泡和太阳的区别都是十分明显的。
Without working in an HDR render environment it's impossible to correctly specify each light's relative intensity.
在没有HDR的渲染环境里,区分各个光源的相对亮度是不可能的。
So, PBR and HDR go hand in hand, but how does it all relate to image based lighting?
所以PBR和HDR携手并进,但是这和IBL有什么关系?
We've seen in the previous tutorial that it's relatively easy to get PBR working in HDR.
我们在前面的教程中看到,在HDR中使用PBR是比较简单的。
However, seeing as for image based lighting we base the environment's indirect light intensity on the color values of an environment cubemap we need some way to store the lighting's high dynamic range into an environment map.
但是,鉴于对IBL我们用环境贴图保存了间接光源的强度,我们需要某种方式将光源的HDR信息存储到一个环境贴图中。
The environment maps we've been using so far as cubemaps (used as skyboxes for instance) are in low dynamic range (LDR).
目前为止我们用于制作cubemap(例如用于天空盒)的环境贴图都是低动态范围(LDR)的。
We directly used their color values from the individual face images, ranged between 0.0 and 1.0, and processed them as is.
我们直接从贴图上取出颜色值(范围为0.0到1.0),然后就这么用了。
While this may work fine for visual output, when taking them as physical input parameters it's not going to work.
这可以得到还凑合的视觉效果,但将它们当作物理参数输入时,就不行了。
The radiance HDR file format辐射度HDR文件格式
Enter the radiance file format. The radiance file format (with the .hdr extension) stores a full cubemap with all 6 faces as floating point data allowing anyone to specify color values outside the 0.0 to 1.0 range to give lights their correct color intensities.
认识一下辐射度文件格式。以.hdr为扩展名,它存储着由6个face组成的cubemap,数据类型为float,数据范围不限于0.0到1.0,从而记录光源的正确颜色强度。
The file format also uses a clever trick to store each floating point value not as a 32 bit value per channel, but 8 bits per channel using the color's alpha channel as an exponent (this does come with a loss of precision).
这个格式还使用了一个聪明的技巧,它不用32位存储一个通道,而是用8位。同时使用alpha通道作指数。(这确实会有精度损失)
This works quite well, but requires the parsing program to re-convert each color to their floating point equivalent.
这很好用,但是要求解析程序将每个颜色值恢复为相等的浮点格式。
There are quite a few radiance HDR environment maps freely available from sources like sIBL archive of which you can see an example below:
有一些辐射度HDR环境贴图供免费使用,例如IBL archive(http://www.hdrlabs.com/sibl/archive.html),下图是一个例子:

This might not be exactly what you were expecting as the image appears distorted and doesn't show any of the 6 individual cubemap faces of environment maps we've seen before.
这可能和你期待的不一样。它被扭曲了,它没有显示6个独立的face。
This environment map is projected from a sphere onto a flat plane such that we can more easily store the environment into a single image known as an equirectangular map.
这个环境贴图是从球体映射到平面上的,这使得我们可以更容易地存储环境信息,这样的贴图被称为球形贴图。
This does come with a small caveat as most of the visual resolution is stored in the horizontal view direction, while less is preserved in the bottom and top directions.
这里确实要警告一下,水平方向上的分辨率高(存储的信息多),顶部和底部存储的分辨率低(存储的信息少)。
In most cases this is a decent compromise as with almost any renderer you'll find most of the interesting lighting and surroundings in the horizontal viewing directions.
大多数时候这是个划算的妥协,因为大多数观察者关注的都是水平方向上的光景。
HDR and stb_image.h
Loading radiance HDR images directly requires some knowledge of the file format which isn't too difficult, but cumbersome nonetheless.
加载辐射率HDR文件需要一些文件格式的知识,这并不难,但是太繁琐。
Lucky for us, the popular one header library stb_image.h supports loading radiance HDR images directly as an array of floating point values which perfectly fits our needs.
幸运的是,广受好评的头文件库stb_image.h支持加载辐射率HDR文件,正好满足我们的需要。
With stb_image added to your project, loading an HDR image is now as simple as follows:
将stb_image加入你的项目中,加载HDR文件就简化如下:
1 #include "stb_image.h" 2 [...] 3 4 stbi_set_flip_vertically_on_load(true); 5 int width, height, nrComponents; 6 float *data = stbi_loadf("newport_loft.hdr", &width, &height, &nrComponents, 0); 7 unsigned int hdrTexture; 8 if (data) 9 { 10 glGenTextures(1, &hdrTexture); 11 glBindTexture(GL_TEXTURE_2D, hdrTexture); 12 glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, width, height, 0, GL_RGB, GL_FLOAT, data); 13 14 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE); 15 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE); 16 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR); 17 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR); 18 19 stbi_image_free(data); 20 } 21 else 22 { 23 std::cout << "Failed to load HDR image." << std::endl; 24 }
stb_image.h automatically maps the HDR values to a list of floating point values: 32 bits per channel and 3 channels per color by default.
stb_image.h自动将HDR值映射为一系列浮点值:默认地,每个通道32位,每个颜色3个通道。
This is all we need to store the equirectangular HDR environment map into a 2D floating point texture.
这就是我们要在球形HDR环境贴图中存储的所有数据。
From Equirectangular to Cubemap从球形贴图到cubemap
It is possible to use the equirectangular map directly for environment lookups, but these operations can be relatively expensive in which case a direct cubemap sample is more performant.
直接将球形贴图用于环境查询是可以的,但是其操作相对耗时。此时,直接用cubemap采样更加高效。
Therefore, in this tutorial we'll first convert the equirectangular image to a cubemap for further processing.
因此,本教程中我们首先将球形贴图转换为cubemap。
Note that in the process we also show how to sample an equirectangular map as if it was a 3D environment map in which case you're free to pick whichever solution you prefer.
注意,在此过程中我们也展示了如何将球形贴图当作3D环境贴图一样采样。你可以采用任何你喜欢的方案。
To convert an equirectangular image into a cubemap we need to render a (unit) cube and project the equirectangular map on all of the cube's faces from the inside and take 6 images of each of the cube's sides as a cubemap face.
为了将球形贴图转换为cubemap,我们需要渲染一个单位立方体,将球形贴图映射到立方体的6个面,然后从立方体内部分别观察6个面,将其作为cubemap的6个face。
The vertex shader of this cube simply renders the cube as is and passes its local position to the fragment shader as a 3D sample vector:
立方体的Vertex Shader只需直接渲染立方体,将其位置当作3D采样向量传送给Fragment Shader:
1 #version 330 core 2 layout (location = 0) in vec3 aPos; 3 4 out vec3 localPos; 5 6 uniform mat4 projection; 7 uniform mat4 view; 8 9 void main() 10 { 11 localPos = aPos; 12 gl_Position = projection * view * vec4(localPos, 1.0); 13 }
For the fragment shader we color each part of the cube as if we neatly folded the equirectangular map onto each side of the cube.
在Fragment Shader中,我们以将球形贴图整洁地折叠映射到立方体上的方式为立方体着色。
To accomplish this, we take the fragment's sample direction as interpolated from the cube's local position and then use this direction vector and some trigonometry magic to sample the equirectangular map as if it's a cubemap itself.
具体如何贴呢?我们以传送来的立方体的位置为采样方向向量,用它再配合一些三角函数,对球形贴图进行采样。
We directly store the result onto the cube-face's fragment which should be all we need to do:
我们需要做的唯一工作就是直接把采样结果存储到立方体的面上:
1 #version 330 core 2 out vec4 FragColor; 3 in vec3 localPos; 4 5 uniform sampler2D equirectangularMap; 6 7 const vec2 invAtan = vec2(0.1591, 0.3183); 8 vec2 SampleSphericalMap(vec3 v) 9 { 10 vec2 uv = vec2(atan(v.z, v.x), asin(v.y)); 11 uv *= invAtan; 12 uv += 0.5; 13 return uv; 14 } 15 16 void main() 17 { 18 vec2 uv = SampleSphericalMap(normalize(localPos)); // make sure to normalize localPos 19 vec3 color = texture(equirectangularMap, uv).rgb; 20 21 FragColor = vec4(color, 1.0); 22 }
If you render a cube at the center of the scene given an HDR equirectangular map you'll get something that looks like this:
如果你在场景中心渲染一个立方体,并给它一个HDR球形贴图,你会得到下图所示的东东:

This demonstrates that we effectively mapped an equirectangular image onto a cubic shape, but doesn't yet help us in converting the source HDR image onto a cubemap texture.
此图展示了我们实际上将球形贴图映射到了一个立方体形状上,但是并没有将其转换为cubemap纹理对象。
To accomplish this we have to render the same cube 6 times looking at each individual face of the cube while recording its visual result with a framebuffer object:
为得到cubemap纹理对象,我们必须渲染这个立方体6次,每次都看向不同的方向,同时,将渲染结果记录到一个帧缓存对象上:
1 unsigned int captureFBO, captureRBO; 2 glGenFramebuffers(1, &captureFBO); 3 glGenRenderbuffers(1, &captureRBO); 4 5 glBindFramebuffer(GL_FRAMEBUFFER, captureFBO); 6 glBindRenderbuffer(GL_RENDERBUFFER, captureRBO); 7 glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512); 8 glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, captureRBO);
Of course, we then also generate the corresponding cubemap, pre-allocating memory for each of its 6 faces:
当然,接下来我们创建cubemap对象,为其分配6个face的内存:
1 unsigned int envCubemap; 2 glGenTextures(1, &envCubemap); 3 glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap); 4 for (unsigned int i = 0; i < 6; ++i) 5 { 6 // note that we store each face with 16 bit floating point values 7 glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 8 512, 512, 0, GL_RGB, GL_FLOAT, nullptr); 9 } 10 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE); 11 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE); 12 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE); 13 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR); 14 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
Then what's left to do is capture the equirectangular 2D texture onto the cubemap faces.
剩下的就是将球形贴图捕捉到cubemap的各个面上。
I won't go over the details as the code details topics previously discussed in the framebuffer and point shadows tutorials, but it effectively boils down to setting up 6 different view matrices facing each side of the cube, given a projection matrix with a fov of 90 degrees to capture the entire face, and render a cube 6 times storing the results in a floating point framebuffer:
在之前的帧缓存和阴影教程中我们讨论过这些代码了,所以这里我不再会详细介绍。这些代码总的来说是,设置6个不同的view矩阵,分别朝向立方体的6个面,给定依据fov为90度的projection矩阵,以此(为摄像机)捕捉立方体的6个面,最后通过渲染6次立方体,将结果保存到浮点型的帧缓存中:
1 glm::mat4 captureProjection = glm::perspective(glm::radians(90.0f), 1.0f, 0.1f, 10.0f); 2 glm::mat4 captureViews[] = 3 { 4 glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 1.0f, 0.0f, 0.0f), glm::vec3(0.0f, -1.0f, 0.0f)), 5 glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(-1.0f, 0.0f, 0.0f), glm::vec3(0.0f, -1.0f, 0.0f)), 6 glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, 1.0f, 0.0f), glm::vec3(0.0f, 0.0f, 1.0f)), 7 glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, -1.0f, 0.0f), glm::vec3(0.0f, 0.0f, -1.0f)), 8 glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, 0.0f, 1.0f), glm::vec3(0.0f, -1.0f, 0.0f)), 9 glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, 0.0f, -1.0f), glm::vec3(0.0f, -1.0f, 0.0f)) 10 }; 11 12 // convert HDR equirectangular environment map to cubemap equivalent 13 equirectangularToCubemapShader.use(); 14 equirectangularToCubemapShader.setInt("equirectangularMap", 0); 15 equirectangularToCubemapShader.setMat4("projection", captureProjection); 16 glActiveTexture(GL_TEXTURE0); 17 glBindTexture(GL_TEXTURE_2D, hdrTexture); 18 19 glViewport(0, 0, 512, 512); // don't forget to configure the viewport to the capture dimensions. 20 glBindFramebuffer(GL_FRAMEBUFFER, captureFBO); 21 for (unsigned int i = 0; i < 6; ++i) 22 { 23 equirectangularToCubemapShader.setMat4("view", captureViews[i]); 24 glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, 25 GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, envCubemap, 0); 26 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); 27 28 renderCube(); // renders a 1x1 cube 29 } 30 glBindFramebuffer(GL_FRAMEBUFFER, 0);
We take the color attachment of the framebuffer and switch its texture target around for every face of the cubemap, directly rendering the scene into one of the cubemap's faces.
我们使用帧缓存的颜色附件,调整纹理目标,从而依次指向cubemap各个face,这样就可以直接将场景渲染到cubemap的各个face上。
Once this routine has finished (which we only have to do once) the cubemap envCubemap should be the cubemapped environment version of our original HDR image.
一旦这段程序执行完(只需执行一次),名字为envCubemap的cubemap对象就成为cubemap版本的HDR环境贴图。
Let's test the cubemap by writing a very simple skybox shader to display the cubemap around us:
让我们测试一下这个cubemap:写一个十分简单的天空盒shader显示出cubemap:
1 #version 330 core 2 layout (location = 0) in vec3 aPos; 3 4 uniform mat4 projection; 5 uniform mat4 view; 6 7 out vec3 localPos; 8 9 void main() 10 { 11 localPos = aPos; 12 13 mat4 rotView = mat4(mat3(view)); // remove translation from the view matrix 14 vec4 clipPos = projection * rotView * vec4(localPos, 1.0); 15 16 gl_Position = clipPos.xyww; 17 }
Note the xyww trick here that ensures the depth value of the rendered cube fragments always end up at 1.0, the maximum depth value, as described in the cubemap tutorial.
注意,这里的xyww小技巧,它保证了立方体的深度值始终是1.0,即最大的深度值。在cubemap教程中我们讲过的。
Do note that we need to change the depth comparison function to GL_LEQUAL:
一定记得我们需要将深度比较函数设置为GL_LEQUAL:
glDepthFunc(GL_LEQUAL);
The fragment shader then directly samples the cubemap environment map using the cube's local fragment position:
然后Fragment Shader直接以立方体的顶点位置为参数,对cubemap类型的环境贴图进行采样:
1 #version 330 core 2 out vec4 FragColor; 3 4 in vec3 localPos; 5 6 uniform samplerCube environmentMap; 7 8 void main() 9 { 10 vec3 envColor = texture(environmentMap, localPos).rgb; 11 12 envColor = envColor / (envColor + vec3(1.0)); 13 envColor = pow(envColor, vec3(1.0/2.2)); 14 15 FragColor = vec4(envColor, 1.0); 16 }
We sample the environment map using its interpolated vertex cube positions that directly correspond to the correct direction vector to sample.
被插值的立方体位置是与要采样的方向向量直接对应的,所以我们才能直接用它作为采样参数。
Seeing as the camera's translation components are ignored, rendering this shader over a cube should give you the environment map as a non-moving background.
你看,由于摄像机的平移数据被忽略了,用这个shader渲染立方体会给你一个不移动的环境贴图。
Also, note that as we directly output the environment map's HDR values to the default LDR framebuffer we want to properly tone map the color values.
另外,注意到我们直接将HDR的环境贴图输出到默认的LDR帧缓存中,我们得适当地调整颜色值。
Furthermore, almost all HDR maps are in linear color space by default so we need to apply gamma correction before writing to the default framebuffer.
此外,几乎所有的HDR贴图默认情况下都处在线性颜色空间,所以我们需要在写入帧缓存前应用伽马校正。
Now rendering the sampled environment map over the previously rendered spheres should look something like this:
现在在渲染球体后渲染环境贴图的结果如下图所示:

Well... it took us quite a bit of setup to get here, but we successfully managed to read an HDR environment map, convert it from its equirectangular mapping to a cubemap and render the HDR cubemap into the scene as a skybox.
好吧,确实耗费好多前期工作才走到这一步。但是,我们成功地读取了一个HDR环境贴图,将其从球形映射形式转换为cubemap纹理对象,并将HDR的cubemap当作天空盒渲染到了场景中。
Furthermore, we set up a small system to render onto all 6 faces of a cubemap which we'll need again when convoluting the environment map.
此外,我们建设了一个小系统,使我们可以分别渲染一些内容到cubemap的6个面。这系统在后续对环境贴图进行卷积时还要用到。
You can find the source code of the entire conversion process here.
你可以在这里(https://learnopengl.com/code_viewer_gh.php?code=src/6.pbr/2.1.1.ibl_irradiance_conversion/ibl_irradiance_conversion.cpp)找到整个转换过程的代码。
Cubemap convolution立方体贴图卷积
As described at the start of the tutorial, our main goal is to solve the integral for all diffuse indirect lighting given the scene's irradiance in the form of a cubemap environment map.
如本教程最开始所述,我们的主要目标是,对场景中cubemap环境贴图形式的辐照度设定的间接光照,求解它们的diffuse部分的积分。
We know that we can get the radiance of the scene L(p, wi) in a particular direction by sampling an HDR environment map in direction wi.
我们知道,我们可以通过在方向wi上对HDR环境贴图采样,来得到场景在此方向上的辐射率L(p, wi)。
To solve the integral, we have to sample the scene's radiance from all possible directions within the hemisphere Ω for each fragment.
为求解积分,我们不得不对半球Ω上的所有可能方向采样其辐射率。
It is however computationally impossible to sample the environment's lighting from every possible direction in Ω, the number of possible directions is theoretically infinite.
对半球Ω上每个可能的方向都采样其环境光,这样的计算量是不可能完成的,因为方向的数量是无限的。
We can however, approximate the number of directions by taking a finite number of directions or samples, spaced uniformly or taken randomly from within the hemisphere to get a fairly accurate approximation of the irradiance, effectively solving the integral ∫ discretely
不过我们可以求解一个近似值。在有限的方向上均匀地或随机地采样,就可以得到一个相当精确的辐照度,实际上就用离散的方式求解了积分∫。
It is however still too expensive to do this for every fragment in real-time as the number of samples still needs to be significantly large for decent results, so we want to pre-compute this.
为了得到像样的近似值,采样的数量必须相当大,这使得在每个Fragment Shader中实时计算这个近似值仍旧太耗时。
Since the orientation of the hemisphere decides where we capture the irradiance we can pre-calculate the irradiance for every possible hemisphere orientation oriented around all outgoing directions wo:
半球的朝向决定了我们在哪里捕捉辐照度。所以,我们可以对每个可能的出射光线方向wo预计算出对应半球的辐照度。
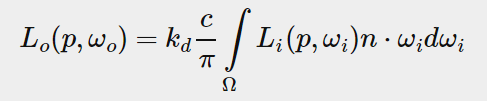
Given any direction vector wi, we can then sample the pre-computed irradiance map to retrieve the total diffuse irradiance from direction wi.
之后,给定任意方向向量wi,我们都可以在预计算的辐照度贴图中检索到此方向上的总的diffuse辐照度。
To determine the amount of indirect diffuse (irradiant) light at a fragment surface, we retrieve the total irradiance from the hemisphere oriented around its surface's normal.
围绕着表面法线的半球上接收到的所有的辐照度,就是一个片段表面上的间接光源的diffuse总量。
Obtaining the scene's irradiance is then as simple as:
获取场景中某处的辐照度就简单地表示如下:
vec3 irradiance = texture(irradianceMap, N);
Now, to generate the irradiance map we need to convolute the environment's lighting as converted to a cubemap.
现在,为生成辐照度贴图,我们需要对环境光进行卷积计算。
Given that for each fragment the surface's hemisphere is oriented along the normal vector N, convoluting a cubemap equals calculating the total averaged radiance of each direction wi in the hemisphere Ω oriented along N.
对每个Fragment,其表面的半球Ω都是朝向法线向量N的。对cubemap卷积等于计算半球Ω的所有方向wi上的辐射度的平均值。

Thankfully, all of the cumbersome setup in this tutorial isn't all for nothing as we can now directly take the converted cubemap, convolute it in a fragment shader and capture its result in a new cubemap using a framebuffer that renders to all 6 face directions.
本教程之前讲述的繁琐的建设又有用了。我们可以直接拿来cubemap,在Fragment Shader中进行卷积,将其结果保存到Framebuffer中的另一个cubemap中。当然了,又要渲染6个face。
As we've already set this up for converting the equirectangular environment map to a cubemap, we can take the exact same approach but use a different fragment shader:
我们已经在将球形环境贴图转换为cubemap时建设过了,现在只需把另一个Fragment Shader用到这个建设过程中即可:
1 #version 330 core 2 out vec4 FragColor; 3 in vec3 localPos; 4 5 uniform samplerCube environmentMap; 6 7 const float PI = 3.14159265359; 8 9 void main() 10 { 11 // the sample direction equals the hemisphere's orientation 12 vec3 normal = normalize(localPos); 13 14 vec3 irradiance = vec3(0.0); 15 16 [...] // convolution code 17 18 FragColor = vec4(irradiance, 1.0); 19 }
With environmentMap being the HDR cubemap as converted from the equirectangular HDR environment map.
变量environmentMap是从球形HDR环境贴图转换来的cubemap对象。
There are many ways to convolute the environment map, but for this tutorial we're going to generate a fixed amount of sample vectors for each cubemap texel along a hemisphere Ω oriented around the sample direction and average the results.
卷积方法有多种,本教程采用其中一种:对每个纹素,生成固定数量的采样向量,然而求平均值。(这句不会翻)
The fixed amount of sample vectors will be uniformly spread inside the hemisphere.
这些数目固定的采样向量会均匀的分布在半球内。
Note that an integral is a continuous function and discretely sampling its function given a fixed amount of sample vectors will be an approximation.
注意,积分是在一个连续函数上定义的,这里离散得采样计算给出的只是一个近似值。
The more sample vectors we use, the better we approximate the integral.
采样向量越多,近似值就越好。
The integral ∫ of the reflectance equation revolves around the solid angle dw which is rather difficult to work with.
反射率方程的积分要对立体角dw进行积分,这是比较困难的。
Instead of integrating over the solid angle dw we'll integrate over its equivalent spherical coordinates θ and ϕ.
我们不对立体角dw积分,而是对它的等价的球坐标θ和ϕ积分。
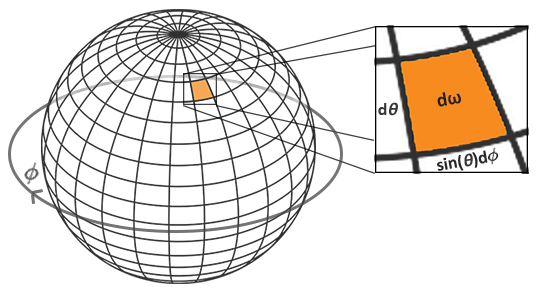
We use the polar azimuth ϕ angle to sample around the ring of the hemisphere between 0 and 2π, and use the inclination zenith θ angle between 0 and π/2 to sample the increasing rings of the hemisphere.
我们用ϕ对半球经线方向采样0到2π度,用θ对半球纬线方向采样0到π/2度。
This will give us the updated reflectance integral:
这就得到了新的反射率方程:
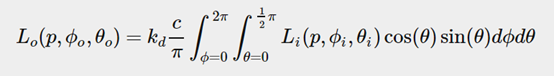
Solving the integral requires us to take a fixed number of discrete samples within the hemisphere Ω and averaging their results.
求积分的过程中,需要将半球Ω上的若干离散采样值相加后求平均值。
This translates the integral to the following discrete version as based on the Riemann sum given n1 and n2 discrete samples on each spherical coordinate respectively:
鉴于在半球坐标上对n1和n2的离散采样是相互独立的,我们可以利用黎曼和公式将上述积分转化为下述形式:
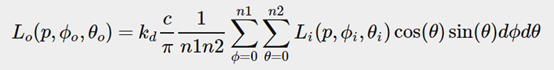
As we sample both spherical values discretely, each sample will approximate or average an area on the hemisphere as the image above shows.
(废话,懒得翻译)
Note that (due to the general properties of a spherical shape) the hemisphere's discrete sample area gets smaller the higher the zenith angle θ as the sample regions converge towards the center top.
注意,(由于球体的形状所致)半球的离散采样面积在比较高的位置上比较小。
To compensate for the smaller areas, we weigh its contribution by scaling the area by sinθ clarifying the added sinsin.
为抵消这个影响,我们用sinθ对采样面积进行加权。
Discretely sampling the hemisphere given the integral's spherical coordinates for each fragment invocation translates to the following code:
对半球的离散采样积分过程,可在Fragment Shader中编码如下:
1 vec3 irradiance = vec3(0.0); 2 3 vec3 up = vec3(0.0, 1.0, 0.0); 4 vec3 right = cross(up, normal); 5 up = cross(normal, right); 6 7 float sampleDelta = 0.025; 8 float nrSamples = 0.0; 9 for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta) 10 { 11 for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta) 12 { 13 // spherical to cartesian (in tangent space) 14 vec3 tangentSample = vec3(sin(theta) * cos(phi), sin(theta) * sin(phi), cos(theta)); 15 // tangent space to world 16 vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N; 17 18 irradiance += texture(environmentMap, sampleVec).rgb * cos(theta) * sin(theta); 19 nrSamples++; 20 } 21 } 22 irradiance = PI * irradiance * (1.0 / float(nrSamples));
We specify a fixed sampleDelta delta value to traverse the hemisphere; decreasing or increasing the sample delta will increase or decrease the accuracy respectively.
我们用sampleDelta变量来调节采样的精确度(稀疏度)。
From within both loops, we take both spherical coordinates to convert them to a 3D Cartesian sample vector, convert the sample from tangent to world space and use this sample vector to directly sample the HDR environment map.
在双循环体内,我们将球坐标转换为3D笛卡尔坐标,再将其从tangent空间转换到世界空间,然后用此坐标为采样向量在HDR环境贴图中采样。
We add each sample result to irradiance which at the end we divide by the total number of samples taken, giving us the average sampled irradiance.
我们将每个采样值都加入辐照度中,最后除以采样数,得到辐照度的平均值。
Note that we scale the sampled color value by cos(theta) due to the light being weaker at larger angles and by sin(theta) to account for the smaller sample areas in the higher hemisphere areas.
注意,光照在角度增加时会减弱,所以我们用cos(theta)对采样值进行缩放,同sin(theta)对球面高处的采样区域进行加权。
Now what's left to do is to set up the OpenGL rendering code such that we can convolute the earlier captured envCubemap.
现在剩下的工作就是建设OpenGL渲染代码,好让那个我们能够对之前捕捉的envCubemap纹理对象进行卷积操作。
First we create the irradiance cubemap (again, we only have to do this once before the render loop):
首先, 我们场景辐照度cubemap对象(只需在渲染循环前执行一次):
1 unsigned int irradianceMap; 2 glGenTextures(1, &irradianceMap); 3 glBindTexture(GL_TEXTURE_CUBE_MAP, irradianceMap); 4 for (unsigned int i = 0; i < 6; ++i) 5 { 6 glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 32, 32, 0, 7 GL_RGB, GL_FLOAT, nullptr); 8 } 9 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE); 10 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE); 11 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE); 12 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR); 13 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
As the irradiance map averages all surrounding radiance uniformly it doesn't have a lot of high frequency details so we can store the map at a low resolution (32x32) and let OpenGL's linear filtering do most of the work.
由于辐照度贴图均匀地记录了周围辐射率的平均值,它并没有多少高频率的细节,所以我们可以用低分辨率(32x32)的贴图来存储,用OpenGL的线性过滤支持细节。
Next, we re-scale the capture framebuffer to the new resolution:
接下来,我们将capture帧缓存缩放为新的分辨率:
1 glBindFramebuffer(GL_FRAMEBUFFER, captureFBO); 2 glBindRenderbuffer(GL_RENDERBUFFER, captureRBO); 3 glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 32, 32);
Using the convolution shader we convolute the environment map in a similar way we captured the environment cubemap:
在卷积shader中,我们对环境贴图的卷积操作类似捕捉cubemap纹理:
1 irradianceShader.use(); 2 irradianceShader.setInt("environmentMap", 0); 3 irradianceShader.setMat4("projection", captureProjection); 4 glActiveTexture(GL_TEXTURE0); 5 glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap); 6 7 glViewport(0, 0, 32, 32); // don't forget to configure the viewport to the capture dimensions. 8 glBindFramebuffer(GL_FRAMEBUFFER, captureFBO); 9 for (unsigned int i = 0; i < 6; ++i) 10 { 11 irradianceShader.setMat4("view", captureViews[i]); 12 glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, 13 GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, irradianceMap, 0); 14 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); 15 16 renderCube(); 17 } 18 glBindFramebuffer(GL_FRAMEBUFFER, 0);
Now after this routine we should have a pre-computed irradiance map that we can directly use for our diffuse image based lighting.
此程序执行后我们就得到了预计算的辐照度贴图,它可以直接用于IBL的diffuse计算。
To see if we successfully convoluted the environment map let's substitute the environment map for the irradiance map as the skybox's environment sampler:
为验证我们是否阵的卷积了环境贴图,我们用它代替天空盒的纹理对象看看:

If it looks like a heavily blurred version of the environment map you've successfully convoluted the environment map.
如果天空盒看起来相当模糊,那就说明你已经成功的卷积了环境贴图。
PBR and indirect irradiance lighting PBR和间接辐照度光照
The irradiance map represents the diffuse part of the reflectance integral as accumulated from all surrounding indirect light.
辐照度贴图描述了反射比积分中的diffuse部分,它将所有周围的间接光照都加了进来。
Seeing as the light doesn't come from any direct light sources, but from the surrounding environment we treat both the diffuse and specular indirect lighting as the ambient lighting, replacing our previously set constant term.
鉴于光并非来自任何直接的光源,而是来自周围的环境,我们将diffuse和specular两种间接光都视为环境光。所以去掉之前的某些常量。
First, be sure to add the pre-calculated irradiance map as a cube sampler:
首先,将cube采样器类型的预计算的辐照度贴图加入进来:
uniform samplerCube irradianceMap;
Given the irradiance map that holds all of the scene's indirect diffuse light, retrieving the irradiance influencing the fragment is as simple as a single texture sample given the surface's normal:
辐照度贴图记录着场景的所有间接diffuse光。检索影响一个Fragment的辐照度,只需用表面的法线对纹理对象采样:
1 // vec3 ambient = vec3(0.03); 2 vec3 ambient = texture(irradianceMap, N).rgb;
However, as the indirect lighting contains both a diffuse and specular part as we've seen from the split version of the reflectance equation we need to weigh the diffuse part accordingly.
然而,我们从反射率方程的拆分版本中也看到了,间接光里包含了diffuse和specular两部分。因此我们需要找到diffuse部分的数量。
Similar to what we did in the previous tutorial we use the Fresnel equation to determine the surface's indirect reflectance ratio from which we derive the refractive or diffuse ratio:
用我们在之前的教程的方法,我们用菲涅耳方程来计算表面的间接反射比,这是从折射率(或者叫反射绿)演化来的:
1 vec3 kS = fresnelSchlick(max(dot(N, V), 0.0), F0); 2 vec3 kD = 1.0 - kS; 3 vec3 irradiance = texture(irradianceMap, N).rgb; 4 vec3 diffuse = irradiance * albedo; 5 vec3 ambient = (kD * diffuse) * ao;
As the ambient light comes from all directions within the hemisphere oriented around the normal N there's no single halfway vector to determine the Fresnel response.
由于环境光来自半球的所有方向,半球围绕着法线,因此找不到单一的半角向量来提供给菲涅耳方程。
To still simulate Fresnel, we calculate the Fresnel from the angle between the normal and view vector.
为了模仿菲涅耳方程,我们将法线和观察者方向的中间向量提供给菲涅耳方程。
However, earlier we used the micro-surface halfway vector, influenced by the roughness of the surface, as input to the Fresnel equation.
然而,之前我们提供给菲涅耳方程的是微平面的半角向量,它受表面的粗糙度影响。
As we currently don't take any roughness into account, the surface's reflective ratio will always end up relatively high.
我们现在不考虑粗糙度,所以表面的反射比总是比较高。
Indirect light follows the same properties of direct light so we expect rougher surfaces to reflect less strongly on the surface edges.
间接光与直接光遵具有同样的属性,所以我们预期更粗糙的表面边缘会反射得比较弱。
As we don't take the surface's roughness into account, the indirect Fresnel reflection strength looks off on rough non-metal surfaces (slightly exaggerated for demonstration purposes):
由于我们不考虑表面的粗糙度,间接非尼尔反射的强度在非金属表面上减弱了不少(为了演示,略微夸张了点效果):

We can alleviate the issue by injecting a roughness term in the Fresnel-Schlick equation as described by Sébastien Lagarde:
拜Sébastien Lagarde大神所赐,我们可以通过想非尼尔方程注入一个粗糙度参数来减轻这个问题:
1 vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness) 2 { 3 return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1.0 - cosTheta, 5.0); 4 }
By taking account of the surface's roughness when calculating the Fresnel response, the ambient code ends up as:
在计算非尼尔方程时考虑了表面的粗糙度,代码就变为了:
1 vec3 kS = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness); 2 vec3 kD = 1.0 - kS; 3 vec3 irradiance = texture(irradianceMap, N).rgb; 4 vec3 diffuse = irradiance * albedo; 5 vec3 ambient = (kD * diffuse) * ao;
As you can see, the actual image based lighting computation is quite simple and only requires a single cubemap texture lookup; most of the work is in pre-computing or convoluting the environment map into an irradiance map.
你看,实际上IBL计算是相当简单的,它只需要一个cubemap纹理查询,大部分工作都在预计算或者卷积环境贴图为辐照度贴图的过程中。
If we take the initial scene from the lighting tutorial where each sphere has a vertically increasing metallic and a horizontally increasing roughness value and add the diffuse image based lighting it'll look a bit like this:
如果我们给之前的光照教程中的场景加入IBL的diffuse,其效果如下图所示:

It still looks a bit weird as the more metallic spheres require some form of reflection to properly start looking like metallic surfaces (as metallic surfaces don't reflect diffuse light) which at the moment are only coming (barely) from the point light sources.
上图框起来仍旧有点诡异。金属度更高的球体需要用反射(specular)来恰当地表现出金属表面(金属表面不反射diffuse光)。而此时的specular光仅仅来源于那4个点光源。
Nevertheless, you can already tell the spheres do feel more in place within the environment (especially if you switch between environment maps) as the surface response reacts accordingly to the environment's ambient lighting.
尽管如此,你可以发掘这些球体感觉起来更像是置身于环境中了(特别是当你替换不同的环境贴图时),因为球体的表面会受到环境光的影响。
You can find the complete source code of the discussed topics here.
你可以在这里(https://learnopengl.com/code_viewer_gh.php?code=src/6.pbr/2.1.2.ibl_irradiance/ibl_irradiance.cpp)找到本教程的完整代码。
In the next tutorial we'll add the indirect specular part of the reflectance integral at which point we're really going to see the power of PBR.
在下一篇教程中,我们将加入反射率方程的间接specular部分。到时候我们就会看到PBR的震撼了。
Further reading参考资料
Coding Labs: Physically based rendering: an introduction to PBR and how and why to generate an irradiance map.
(http://www.codinglabs.net/article_physically_based_rendering.aspx)PBR简介,如何以及为何生成辐照度贴图。
The Mathematics of Shading: a brief introduction by ScratchAPixel on several of the mathematics described in this tutorial, specifically on polar coordinates and integrals.
ScratchAPixel编写,对本教程中使用的数学概念的简介,包括极坐标和积分。
总结
不能有一点点不清楚的地方。