用PCA(主成分分析法)进行信号滤波
此文章从我之前的CSDN上导入,代码什么的可以参考matlab官方帮助文档
现在网上大多是通过PCA对数据进行降维,其实PCA还有一个用处就是可以进行信号滤波。网上对此的介绍比较少,正好最近研究了一下,所以把自己的理解记录下来。
对于PCA原理的介绍网上已经有很多帖子,我比较喜欢的是这个:PCA的数学原理。文章把PCA降维定性和数学理解分析得生动且透彻,这里不再重复。
更新:关于PCA的介绍也可以看我的这个:降维方法PCA与SVD的联系与区别
直接上干货吧,简单一个例子:
给定信号: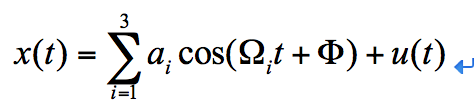
其中有用信号为三个频率不同且幅值相位不相同的余弦函数之和,我把它设为20,30,50HZ,幅值分别为1,2,3。噪声信号u(t)为高斯白噪声,我们现在要用主成分分析将高斯白噪声从x(t)中滤掉。
取100个样本x(t),每个样本的采样点数为1000,也就是1000维(我们可以将维度理解成采样点数,至于为什么维度跟采样点数有关,也许只是正好在数学带入上呈现出相同的形式)。将这100个样本组合成100×1000的矩阵D。这100个样本中间,包含着有用信号与噪声信号两个成分。我们可以把有用信号理解为我们的主要维度A,它的“能量”是比较大的,且可以用方差表示。而噪声信号可以理解成其他维度,与有用信号彼此不是很相关,但是还是有那么一丝的相关性。我们要做的滤波,也就是去噪,就是让他们彼此之间的维度不相关,然后去掉多余的维度,只留下有用信号。
PCA的实现过程是比较规范化的:首先,求矩阵D的协方差矩阵B,协方差矩阵是个很有用的东西,他的对角线上表示的是各样本的方差,也可以理解为各维度的能量,对角线之外的元素表示不同维度之间的内积,也可以理解为相关程度。
然后,我们要讲不同维度的相关程度置0,这里可以用协方差矩阵的对角化得到。这样,我们得到的新维度两两之间就没有相关性了。然后,我们将得到的对角矩阵的特征值从大到小排列,刚才说了,对角线上特征值的大小表示相应维度的能量,表示不同维度对原信号的贡献率。
可以看到,第一主成分,也可以说在这个维度下,它的贡献率(特征值、方差、能量)最高,所以我们可以把它理解为这个主成分包含最多的有用信号。而其他维度分别以很小的,彼此不相关的形式存在着,恰恰跟高斯白噪声的性质很像,所以其他主成分我们可以在滤波中把他们去掉。
这跟降维还是有一定区别的。降维是指累计贡献率达到某个阈值,将阈值之内的主成分(维度)用来还原原始信号(有用信号+噪声信号),他更多的强调一种信号的降维还原。而滤波主要是将原来与有用信号中不相关的部分滤掉,不是一种单纯的无损还原。
所以,我们取第一主成分就够了嘛,是不是!还原出来的信号如下图:
感觉还是不错的,然后我又跟FIR滤波器对比了一下,下面是他们分别的频域图:
还是可以看出明显区别的,因为FIR滤波只能滤除截止频率之外的频率分量,而PCA可以把与主成分没关系的量统统滤除。但是,PCA的局限性也就突显出来:他只能滤出与有用信号不相关的信号,对于相关或略有相关的信号,PCA显得就比较吃力了。



