opencv —— normalize 矩阵归一化

归一化：就是将数据通过某种算法，限制需要的一定范围内。

归一化的目的：简而言之，是使得没有可比性的数据变得具有可比性，同时又保持相比较的两个数据之间的相对关系，如大小关系；或是为了作图，原来很难在一张图上作出来，归一化后就可以很方便的给出图上的相对位置等。

矩阵归一化：normalize 函数

void normalize(InputArry src,InputOutputArray dst,double alpha = 1,double beta = 0,int norm_type = NORM_L2,int dtype = -1,InputArray mark = noArry())

• src，输入图像，Mat 类对象即可。
• dst，函数调用后的结果存在这里，和原图像具有一样的尺寸和类型。
• alpha，①值归一化，表示所乘系数；②范围归一化，表示范围界限，一般当作下界。
• beta，仅范围归一化用到，表示范围另一界限。
• norm_type，归一化选择的数学公式。

NORM_L1:（占比）

 

 

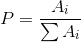
NORM_INF:

 

 

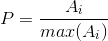
NORM_L2:

 

 

NORM_MINMAX: A_k 不属于{ max(A_i) , min(A_i) },当 A_K 等于 max(A_i) 时 p = 1，等于 min(A_i) 时 p = 0 

 

 

 

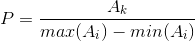
• dtype，为负时，输出图像深度等于输入图像，否则深度为 dtype 类型。一般选择默认值。
• mark，掩码。若有感兴趣区域，则只对该区域进行操作。

 

值归一化：所有 NORM_XXX 公式均可使用

alpha ！= 0，beta = 0，根据数学公式计算出来的所有值均 * alpha。

示例：alpha = 45

 

 

 

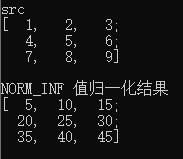
范围归一化：必须且仅可以使用 NORM_MINMAX 公式

alpha ！=0，beta ！= 0，假设 alpha < beta,即归一化范围 [alpha,beta]，简记为 [a,b]。

1. 首先找到样本数据的最小值 Min 及最大值 Max
2. 计算系数为：k =（b - a) / (Max - Min)
3. 得到归一化到 [a,b] 区间的数据：

 示例：alpha = 10，beta = 45

 

（呀呀，网上好多相关文章，但看完还是迷糊，现在终于明白了，(●'◡'●) 开心！）