opencv —— SURF 特征点检测

SURF 算法概述

SURF，英文全称为 SpeededUp Robust Features，直译为“加速版的具有鲁棒性的特征”算法，由 Bay 在 2006 年首次提出。SURF 最大特征在于采用了 harr 特征以及积分图像的概念，这大大加快了程序的运行时间。SURF 可以应用于计算机视觉的物体识别以及 3D 重构中。

SURF 算法原理

SURF 算法主要包含 7 步：

1. 构建 Hessian 矩阵
2. 构建尺度空间
3. 生成 Hessian 行列式图像
4. 利用非极大值抑制初步确定特征点 
5. 精确定位极值点
6. 计算特征点的主方向
7. 生成特征点描述算子

• 构建 Hessian 矩阵

Hessian 矩阵是 Surf 算法的核心。在数学中，Hessian 矩阵是一个二阶偏导数组成的方块矩阵，描述了函数的局部曲率。对于图像 f(x,y) ,其 Hessian 矩阵 为

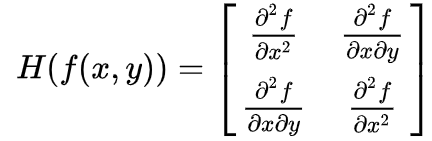
但噪声的存在可能会引起像素突变，所以在构造 Hessian 矩阵前需要对图像进行高斯滤波，经过滤波后的图像为 L(x，σ)，Hessian 矩阵表述为：

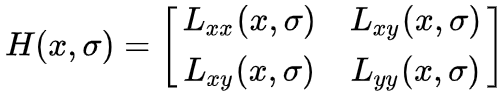
Hessian 矩阵的判别式为：

 

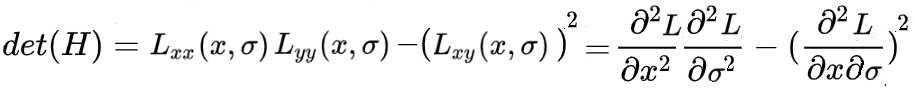
当判别式在（x，y）位置上取得局部极大值或极小值时（当前点比周围邻域内其他点更亮或更暗），（x，y）为关键点位置。

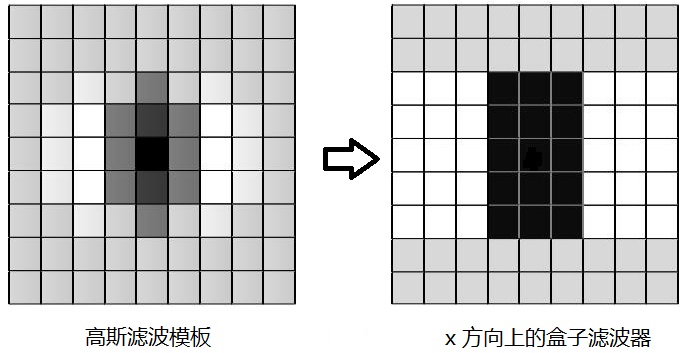
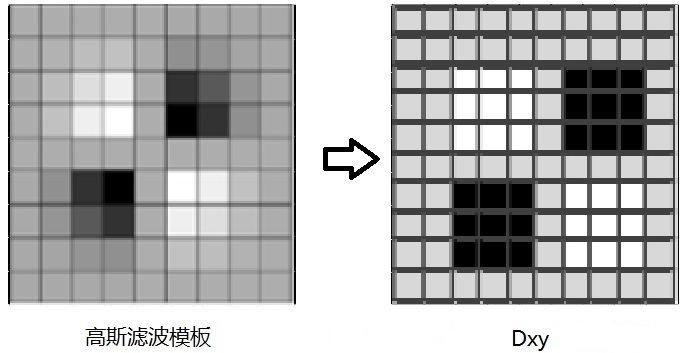
为了提高运算速度，Surf使用了盒式滤波器（Boxfilter）来近似替代高斯滤波器。盒式滤波器（Boxfilter）将对图像的滤波转化成计算图像上不同区域间像素和的加减运算问题，只需要简单几次查找积分图就可以完成。https://www.cnblogs.com/bjxqmy/p/12294444.html

 

其中，Dxy 乘上 0.9，目的是为了平衡因使用盒式滤波器近似所带来的误差，而 0.9 是论文作者给出的一个经验值。

• 构建尺度空间

SIFT 算法通过下采样的方式来获取不同尺度的图像。在 SURF 中，我们保持图像大小不变，通过改变滤波窗口的大小来获得不同尺度的图像，即构成尺度空间。初始的盒子滤波器是 σ 为 1.2 的高斯二阶微分函数经过离散和减裁后的滤波模板。

 

 

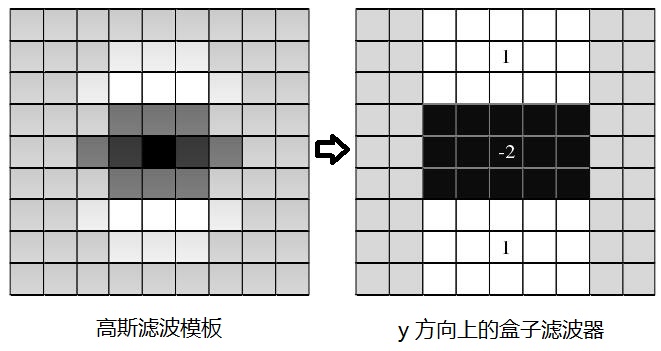
• 生成 Hessian 行列式图像

Bay 建议将尺度空间分为四组，每组中包括四层。每一层对应的 σ 与滤波模板尺寸之间的关系式为：。

每一组中任意一层都包括 D_x D_y D_xy 三种盒子滤波器。对一幅输入图像进行滤波后通过 Hessian 行列式计算公式可以得到对应尺度坐标下的 Hessian 行列式的值。

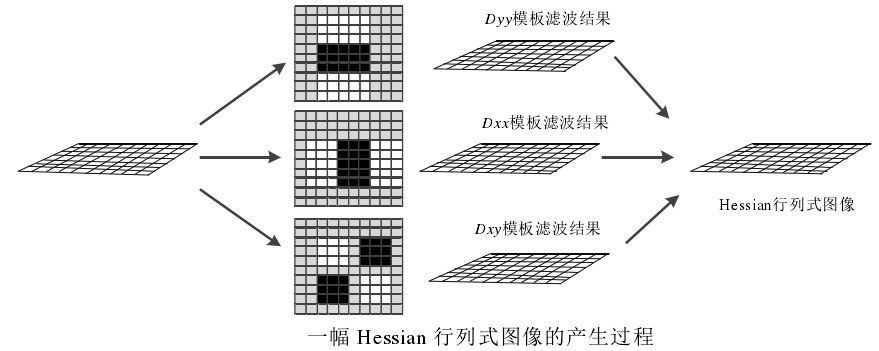
• 利用非极大值抑制初步确定特征点 

在每一组中选取相邻的三层 Hessian 行列式图像，对于中间层的任意一点，在空间中选取该点周围的 26 个点进行比较大小，

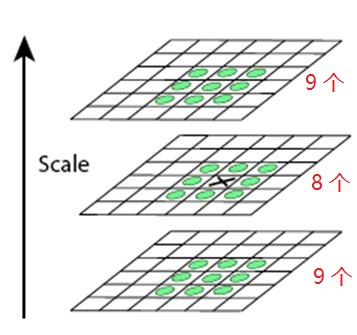
若该点大于其他 26 个点，则该点为特征点。从上述过程可以知道，当尺度空间每组由四层构成时，非极大值抑制只会在中间两层进行，相邻的组之间不进行比较。

• 精确定位极值点

设定 Hessian 行列式的阀值，低于 Hessian 行列式阀值的点不能作为最终的特征点。在实际选择阀值时，根据实际应用中对特征点数量和精确度的要求改变阀值。阀值越大，得到的特征点的鲁棒性越好。在处理场景简单的图像时，其阀值可以适当的调低。在复杂的图像中，图像经旋转或者模糊后特征点变化的数量较大，测试需要适当提高阀值。

• 计算特征点的主方向

① 首先，赋予每一个兴趣点方向特征：在以某个兴趣点为圆心，6S（S为该特征尺度）为半径的圆形领域里，用尺寸为 4S 的 Haar 小波模板对图像进行处理，求 x,y 两个方向的 Haar 小波响应。然后用以兴趣点为中心的高斯函数（σ = 2 s）对这些响应进行加权，结果即为某个兴趣点的方向特征。

Haar 小波的模板如图所示：

其中左侧模板计算 x 方向的响应，右侧模板计算 y 方向的响应，黑色表示 -1，白色表示 +1。

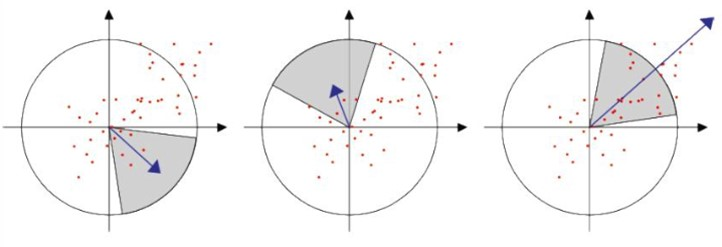
② 然后，在特征点的圆形邻域内，统计 60 度扇形内所有点的方向特征总和，接着扇形以一定间隔进行旋转并再次统计该区域内所有点的方向特征总和，最后将值最大的那个扇形的方向作为该特征点的主方向。

•  生成特征点描述算子

在SURF中，我们在关键点周围选取一个正方形框，方向为关键点的主方向，边长为 20S。将其划分为 16 个区域（边长为 5S），每个区域统计 25S 个像素的水平方向和垂直方向的 Haar 小波特性（均相对于正方形框的主方向确定的）

该小波特征包括水平方向值之和，水平方向绝对值之和，垂直方向值之和和垂直方向绝对值之和（为了把强度变化的极性信息也包括描述符中，所以对绝对值进行累加）。这样每个区域有 4 个值，则每个正方形框有 4×16 = 64 维，即每个关键点描述是 64 维，比SIFT描述少了一半。

 

总结

SURF 采用 Hessian 矩阵获取图像局部最值十分稳定，但是在求主方向阶段太过依赖于局部区域像素的梯度方向，有可能使找到的主方向不准确。而后面的特征向量提取以及匹配又都严重依赖于主方向，可能造成偏差的进一步加大，从而使匹配不成功。另外图像金字塔的层取的不够紧密也会造成尺度的误差，发明者在这个问题上的这种解决办法是取适量的层，然后进行插值。

opencv4.0 及 4.0 以上版本已经没有 SIFT 和 SURF 算法了，他们因为专利的原因不能用于商业。所以不做代码演示了，用到的时候再说吧。

借鉴博客：https://www.cnblogs.com/jinjidexuetu/p/90ace4e8de574e3d5f4e6ac16a0dc157.html

https://www.cnblogs.com/gfgwxw/p/9415218.html

https://blog.csdn.net/Gordon_Wei/article/details/88920411?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task