1.直接使用 stl 中的 next_permutation 实现全排列
#include<bits/stdc++.h>
using namespace std;
int main()
{
int a[4] = {2,4,12,3};
sort(a,a+4);
do
{
for(int i=0;i<4;i++)
{
printf("%d ",a[i]);
}
printf("
");
}while(next_permutation(a,a+4));
}
2.递归求全排列
n 个元素的全排列 =(不断将每个元素作为前缀)+(剩下 n-1 个元素的全排列)
结束:只有一个元素的全排列
#include<bits/stdc++.h>
using namespace std;
int a[4] = {2,4,12,3};
void Swap(int* x,int* y)
{
int temp;
temp = *x;
*x = *y;
*y = temp;
}
int Perm(int begin, int end)
{
if(begin == end)//输出当前全排列
{
for(int i=0;i<4;i++)
{
printf("%d ",a[i]);
}
printf("
");
}
else
{
for(int i=begin;i<=end;i++)
{
Swap(a+begin, a+i);//不断将每个元素作为前缀
Perm(begin+1, end);//剩下 n-1 个元素的全排列
Swap(a+begin, a+i);
}
}
}
int main()
{
sort(a,a+4);
Perm(0, 3);
}
例1:五星填数
在五星图案节点填上数字:1~12,不包括7和11。要求每条直线上数字和相等。
如图就是一个恰当的填法。请搜索所有可能的填法有多少种。
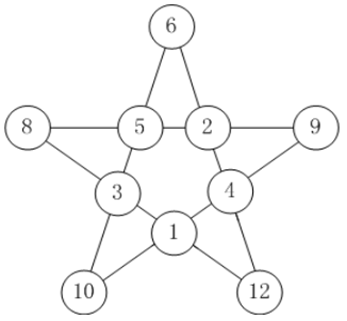
注意:旋转或镜像后相同的算同一种填法。
思路:
第一步:写出10个数的全排列。
第二步:判断每个直线上的数字和是不是相等。
第三步:剔除旋转、镜像相同的解。
旋转:一个解旋转5次,都相同;
镜像:需再除以 2 。
所以最后结果应该除以 10 。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int star[11] = {0,1,2,3,4,5,6,8,9,10,12};
int num = 0;
do
{
int A = star[1] + star[3] + star[6] + star[9];
int B = star[1] + star[4] + star[7] + star[10];
int C = star[2] + star[3] + star[4] + star[5];
int D = star[2] + star[6] + star[8] + star[10];
int E = star[5] + star[7] + star[8] + star[9];
//判断每个直线上的数字和是不是相等
if((A == B)&&(A == C)&&(A == D)&&(A == E))
{
num++;
}
}while(next_permutation(star+1, star+11));
printf("%d", num/10);
}
例2:打印 n 个数中任意 m 个数的全排列
只需修改递归程序中的一个地方即可。
if(begin == m) {//把 Perm()函数中的 end 改为 m 即可。
.......
}
例3:打印 n 个数中任意 m 个数的组合
二进制法求子集:一个二进制数对应一个子集,二进制数中的每个 1 ,都对应了集合中的某个元素。

如何判断二进制数中 1 的个数?
k = k & (k - 1) 能消除二进制数 k 的最后一个 1。
例如:7 的二进制是 111
111 & (111 - 1) = 111 & 110 = 110
110 & (110 - 1) = 110 & 101 = 100
100 & (100 - 1) = 100 & 011 = 000
#include<bits/stdc++.h>
using namespace std;
int a[5] = {11, 4, 2, 3, 8};
void print_set(int n, int m)
{
//0-2^n
for(int i=0;i<(1<<n);i++)
{
int num = 0, k = i;
//统计1的个数
while(k)
{
k = k&(k-1);
num++;
}
if(num == m)
{
//按位与
for(int j=0;j<n;j++)
{
if(i&(1<<j))
{
printf("%d ", a[j]);
}
}
printf("
");
}
}
}
int main()
{
sort(a, a+5);
print_set(5, 3);
}
借鉴博客:https://blog.csdn.net/fox64194167/article/details/20692645