【IDA*】hdu 1560 DNA sequence

题目描述：

http://acm.hdu.edu.cn/showproblem.php?pid=1560

 

中文大意：

用户会给出 N 条 DNA 序列，要求我们计算出一条尽可能短的 DNA 序列，使其包含所有给定序列。

给定序列的嘌呤、嘧啶可以分开，但前后关系不能变。

 

思路：

从第 0 位开始，逐位设置最短 DNA 序列。

而每个位置，有且仅有 4 种选择：A C G T。

选择依据是：该嘌呤或嘧啶是否是某条基因片段剩余部分的首个字母。

例如下图中，最短 DNA 序列的第 3 位，可设置为 G 或 T。

 

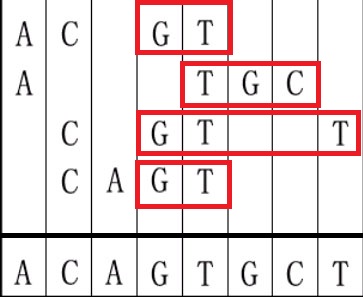
假设当前位置设置为了 G，则:

第一条基因片段的剩余部分变成了“T”，

第二条的剩余部分不变，仍然为“TGC”,

第三条的剩余部分变成了“TT”，

第四条的剩余部分变成了“T”。

接着，我们去设置最短序列的第 4 位，以此类推，直至处理完所有基因片段。

回溯回来后，再尝试将第三位设置成 T，展开新的深搜。

 

代码：

#include<bits/stdc++.h>
using namespace std;

int n;
string str[8];//n 条 DNA 序列 
char DNA[4] = {'A', 'C', 'G', 'T'};
int pos[8];//各 DNA 序列当前的处理位置 
int depth;//深搜深度 
bool have_result;//是否有解 

//index:填写最短序列的第 index 位 
void dfs(int index){
    //剪枝:
    //1.超过深搜限制深度 
    if(index > depth){
        return;
    }
    //2.找到正确答案 
    if(have_result){
        return;
    }
    //n 条DNA序列剩余部分的最大长度 
    int max_surplus = 0;
    for(int i=0;i<n;i++){
        int surplus = str[i].length() - pos[i];
        if(surplus > max_surplus){
            max_surplus = surplus;
        }
    }
    //3.估价函数：已搜层数 + 预搜层数 > 限制深度 
    if(index+max_surplus > depth){
        return;
    }
    //4.没有剩余基因片段了，即找到了一组解 
    if(max_surplus == 0){
        have_result = true;
        return;
    }
    
    //pos为公共数据，每次深搜回溯后，需要保持其值不变，故提前复制一份 
    int pre_pos[8];
    memcpy(pre_pos, pos, sizeof(pos));
    //最短序列的当前位置可以为：A 或 C 或 G 或 T 
    for(int k=0;k<4;k++){
        //选择依据：DNA[k] 是当前某条基因片段剩余部分的首个字母 
        bool appear = false;
        for(int i=0;i<n;i++){
            int j = pos[i];
            if(j < str[i].length() && str[i][j] == DNA[k]){
                appear = true; 
                pos[i]++;
            }
        }
        
        if(appear){
            dfs(index+1);
        }
        //恢复 pos 
        memcpy(pos, pre_pos, sizeof(pre_pos));
    }
}

int main(){
    int t;
    cin>>t;
    while(t--){
        cin>>n;
        depth = -1;
        for(int i=0;i<n;i++){
            cin>>str[i];
            
            //最长基因片段肯定 ≤最短序列的长度，故可以直接将其作为起始深度 
            if(depth < str[i].length()){
                depth = str[i].length();
            }
        }
        
        memset(pos, 0, sizeof(pos));
        have_result = false;
        while(true){
            dfs(0);
            if(have_result){
                break;
            }
            //深度不断增加 
            depth++;
        }
        cout<<depth<<endl;
    }
}