常用的数据结构:
数组:
- 内存连续的,使用时需要初始化大小;
- 可以通过下标来查找到数据,所以查询效率很高,时间复杂度O(1)
- 增删效率比较低,要移动元素或者扩容,时间复杂度O(N)(还要动态扩容,不然会越界)
链表:
- 对内存空间使用比较灵活,内存不需要连续;
- 不支持下标查找,所以查询需要顺序遍历,时间复杂度O(n)
- 增删效率高,最需要操作节点的前后节点的关系,不需要移动元素,时间复杂度O(n)
二叉树:
- 二分的思想,查询的时间复杂度是O(log n);
- 某节点的左子树节点值仅包含小于该节点值;
- 某节点的右子树节点值仅包含大于该节点值;
- 左右子树每个也必须是二叉查找树
- 顺序排列
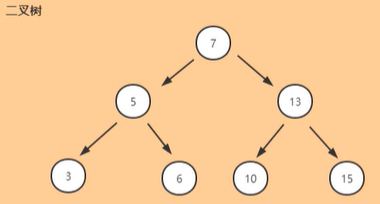
问题:普通二叉树可能会不平衡,甚至链化,查询效率不高,所以我们需要采取一些措施
红黑树:拆去顶端优势来达到平衡的目的。自平衡的二叉树(不是绝对平衡)
规则:
- 每个节点要么是红色、要么是黑色
- 根节点必须是黑色
- 每个叶子节点(NULL)是黑色
- 每个红色节点的两个子节点必须是黑色的(不存在两个相邻的红色节点)
- 任意节点到每个叶子节点的路径都包含相同数量的黑节点(严格来说是黑平衡二叉树)
实现:变色+旋转(左旋、右旋)
左旋:节点往左旋转,即右节点变为相对根节点,该节点变为右节点的左节点。
右旋:节点往右旋转,即左节点变为相对根节点,该节点变为右节点的左节点。

如下图:由上可知,新节点刚插入肯定是红节点,P是父节点,PP是祖父节点,S叔叔节点
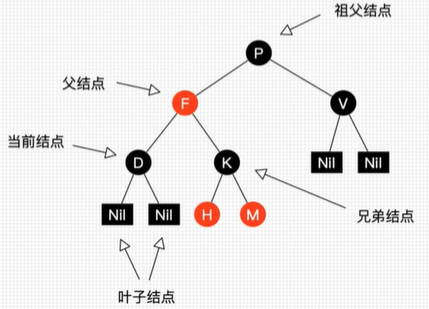
具体案例可参照:https://www.cnblogs.com/deusjin/p/14620791.html
B+树:多路平衡二叉树。(Mysql里介绍)
集合
ArrayList:
本质是数组,底层是基于数组的,会自动扩容(默认10,此后扩容1.5倍,即加右移一位)。
源码分析:
重要的成员变量:
// 初始容量的默认值 private static final int DEFAULT_CAPACITY = 10; // 空的数组,无参构造会初始化一个空数组 private static final Object[] EMPTY_ELEMENTDATA = {}; // 空的数组,无参构造会初始化一个空数组 private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {}; // 集合中存储元素的对象 transient Object[] elementData; // 数组的大小 private int size;
无参构造:
public ArrayList() { this.elementData = DEFAULTCAPACITY_EMPTY_ELEMENTDATA; }
有参构造:
public ArrayList(int initialCapacity) { if (initialCapacity > 0) { // 初始化内部数组,创建指定大小的数组 this.elementData = new Object[initialCapacity]; } else if (initialCapacity == 0) { // 0时,赋值空 this.elementData = EMPTY_ELEMENTDATA; } else { throw new IllegalArgumentException("Illegal Capacity: "+ initialCapacity); } }
Add方法:
public boolean add(E e) { // 确定容量、动态扩容数组 ensureCapacityInternal(size + 1); // 元素加到内部数组里面 elementData[size++] = e; return true; }
继续看ensureCapacityInterna方法:
private void ensureCapacityInternal(int minCapacity) { // 数组为空时,返回默认值10 if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) { minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity); } ensureExplicitCapacity(minCapacity); }
继续看ensureExplicitCapacity方法:

继续看grow方法:

get()方法:

Set()方法:

Remove方法

Failfast机制:内部会维护一个modCount,一旦修改了元素,都会加一,每次遍历元素操作会比较modCount,不是预期值,则抛出返回异常 ,是集合类为了应对并发访问时的原子性,内部结构发生变化的一种防护措施。
,是集合类为了应对并发访问时的原子性,内部结构发生变化的一种防护措施。
LinkedList:
是通过双向链表来实现的,它具有双向链表的优缺点
它的顺序访问效率高,随机访问效率低。
增删效率高
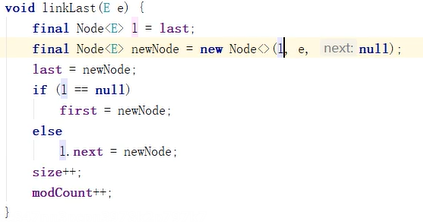
Push方法是加到头部,add加到尾部,源码也就是使用了双向链表
节点加到头部:

节点加到尾部:
Get方法:

Set方法:

Vector
线程安全的,内部实际上是在每个方法上加了synchronized关键字,对性能有比较大的影响。不推荐使用。
java.util.Collections下的synchronizedList方法,可以转化为同步的集合,在代码中可以灵活使用。synchronizedList内部转化为一个同步集合,实际上是使用了同步代码块来实现的。

HashSet
实现了Set接口,使用哈希表来实现,实际上内部是通过HashMao来实现的
存储的数据是无序的,不重复的,允许元素为空。

Set方法是将数据保存在内部的HashMap中,key是我们添加的内容,value就是我们定义的一个Object对象:

TreeSet
基于TreeMap的NavigableSet实现,使用元素的自然顺序来排序,或者由set提供的Comparator继续排序,具体取决于使用什么构造方法

本质是将数据保存在TreeMap中,key是内容,value是一个通用对象。
TreeMap
本质上是红黑树的实现,遵循红黑树的特点。

Put方法:
public V put(K key, V value) { Entry<K,V> t = root; // 根节点 if (t == null) { // 根节点是null compare(key, key); // type (and possibly null) check root = new Entry<>(key, value, null);// 封装node,并设为root size = 1; modCount++; return null; } int cmp; Entry<K,V> parent; // 父节点 // split comparator and comparable paths Comparator<? super K> cpr = comparator; // 比较器 if (cpr != null) { do { // 将root赋值给了parent parent = t; cmp = cpr.compare(key, t.key); // 比较大小 if (cmp < 0) // 小于 t = t.left; //往树的左边走 else if (cmp > 0) t = t.right; // 往树的右边走 else return t.setValue(value); // 在树里面找到直接修改值 } while (t != null); // 循环,继续往下遍历 } else { // 比较器为空 if (key == null) throw new NullPointerException(); @SuppressWarnings("unchecked") Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; cmp = k.compareTo(t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); }// parent就是我们要插入的节点的父节点 // e是封装的节点 Entry<K,V> e = new Entry<>(key, value, parent); if (cmp < 0) parent.left = e; // 插入的节点在parent左侧 else parent.right = e; // 插入的节点在parent右侧 fixAfterInsertion(e); // 实现了红黑树的平衡 size++; modCount++; return null; }
fixAfterInsertion方法:(参照之前的红黑树列举的情况)
private void fixAfterInsertion(Entry<K,V> x) { x.color = RED; // 设置新的节点为红色 // 循环的条件:添加的节点部位空,不是root节点,父节点为红色 while (x != null && x != root && x.parent.color == RED) { // 父节点是否为祖父节点的左侧 if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { // 获取祖父节点节点的右侧,即叔叔节点 Entry<K,V> y = rightOf(parentOf(parentOf(x))); if (colorOf(y) == RED) { // 叔叔节点为红色 setColor(parentOf(x), BLACK); // 设置父节点为黑 setColor(y, BLACK); // 设置叔叔节点为黑 setColor(parentOf(parentOf(x)), RED);//设置祖父为红 x = parentOf(parentOf(x));// 将祖父节点设为插入节点 (往上循环遍历) } else { // 叔叔节点是黑色 // 判断插入节点是否是父节点的右侧节点 if (x == rightOf(parentOf(x))) { // 将父节点作为插入节点 x = parentOf(x); rotateLeft(x);// 左旋 } setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateRight(parentOf(parentOf(x)));// 右旋 } } else { // 父节点是否为祖父节点的左侧 Entry<K,V> y = leftOf(parentOf(parentOf(x))); if (colorOf(y) == RED) { //叔叔节点为红色 setColor(parentOf(x), BLACK); // 父节点变黑色 setColor(y, BLACK); // 叔叔节点变为黑色 setColor(parentOf(parentOf(x)), RED); //设置祖父为红 x = parentOf(parentOf(x)); } else { //叔叔节点为黑色 if (x == leftOf(parentOf(x))) { // 插入节点在右侧 x = parentOf(x); // 将父节点作为插入节点 rotateRight(x); // 右旋 } setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateLeft(parentOf(parentOf(x))); // 左旋 } } } root.color = BLACK; // 根节点为黑色 }
HashMap
底层:1.7采用数组加链表
1.8之后采用数据加链表或者数据加红黑树来实现元素的存储的
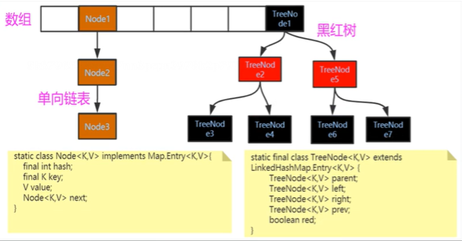
源码分析:
常用的成员变量:
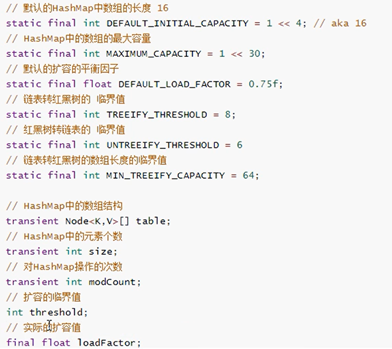
HashMap类里面有个Node<K,V>静态内部类,里面包含四个属性:hash,calue,value,next代码如下(主要看有注释的那四行,其他可以忽略)

接下来看一下put方法的源码:
public V put(K key, V value) { return putVal(hash(key), key, value, false, true); }
这里的hash(key)是计算出key所对应的hash值,

右移16位的原因,减少哈希碰撞的次数,保证散列分布均匀
继续看putVal()方法:
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; // 这里的tab就是table,后三行会赋值,下面我会直接说table而不是tab Node<K,V> p; // p就是table[i],后面也会赋值的 int n, i; if ((tab = table) == null || (n = tab.length) == 0) // table是否为空或者长度为0 n = (tab = resize()).length; //满足则调用resize()方法扩容 if ((p = tab[i = (n - 1) & hash]) == null) // 计算出索引i,如果table[i] == null tab[i] = newNode(hash, key, value, null); // 直接插入 else { // 如果table[i] !=null Node<K,V> e; K k; if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) //判断key是否存在了 e = p; //满足则直接覆盖旧值 else if (p instanceof TreeNode) // key不存在,继续判断是否table[i]是否是TreeNode(红黑树结构) e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); //满足则在红黑树中插入键值对 else { // 不是红黑树结构 // 开始遍历表,并且插入 for (int binCount = 0; ; ++binCount) { if ((e = p.next) == null) { p.next = newNode(hash, key, value, null); if (binCount >= TREEIFY_THRESHOLD - 1) //如果链表长度大于等于8 treeifyBin(tab, hash); // 链表转化为红黑树 break; } if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) // 如果链表中存在相同的key,直接覆盖旧值 break; p = e; } } if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; if (++size > threshold) // 容量达到阀值 resize(); //扩容 afterNodeInsertion(evict); // 这个方法HashMap里面是空的,LinkedHashMap有实现方法,意思就是为了实现顺序插入 return null; }
具体分析看下面的图:
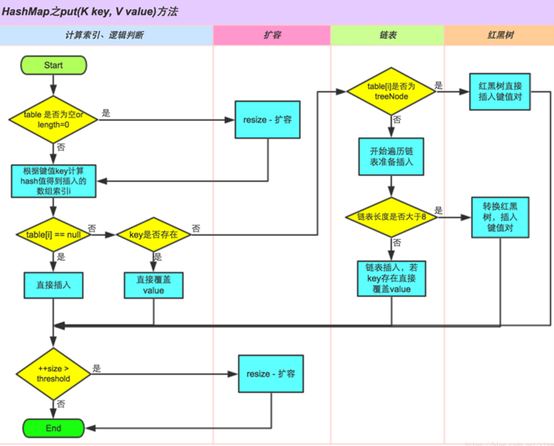
接下来看一下gēt方法的源码:
public V get(Object key) { Node<K,V> e; return (e = getNode(hash(key), key)) == null ? null : e.value; //指定key 通过hash函数得到key的hash值 }
上面的内部getNode()方法是根据hash值,知道对应的Node,并返回。然后就可以获得到里面的value值了。
4.一些问题:
1.HashMap中的碰撞探测(collision detection)以及碰撞的解决方法:
当两个对象的hashcode相同时,它们的bucket位置相同,‘碰撞’会发生。因为HashMap使用LinkedList存储对象,这个Entry(包含有键值对的Map.Entry对象)会存储在LinkedList中。这两个对象就算hashcode相同,但是它们可能并不相等。 那如何获取这两个对象的值呢?当我们调用get()方法,HashMap会使用键对象的hashcode找到bucket位置,遍历LinkedList直到找到值对象。找到bucket位置之后,会调用keys.equals()方法去找到LinkedList中正确的节点,最终找到要找的值对象使用不可变的、声明作final的对象,并且采用合适的equals()和hashCode()方法的话,将会减少碰撞的发生,提高效率。不可变性使得能够缓存不同键的hashcode,这将提高整个获取对象的速度,使用String,Interger这样的wrapper类作为键是非常好的选择。
2.解决 hash 冲突的常见方法
a. 链地址法:将哈希表的每个单元作为链表的头结点,所有哈希地址为 i 的元素构成一个同义词链表。即发生冲突时就把该关键字链在以该单元为头结点的链表的尾部。
b. 开放定址法:即发生冲突时,去寻找下一个空的哈希地址。只要哈希表足够大,总能找到空的哈希地址。
c. 再哈希法:即发生冲突时,由其他的函数再计算一次哈希值。
d. 建立公共溢出区:将哈希表分为基本表和溢出表,发生冲突时,将冲突的元素放入溢出表。
HashMap 就是使用链地址法来解决冲突的(jdk8中采用平衡树来替代链表存储冲突的元素,但hash() 方法原理相同)。数组中的每一个单元都会指向一个链表,如果发生冲突,就将 put 进来的 K- V 插入到链表的尾部。