浅谈拓扑排序

今天来讲讲拓扑排序

度娘告诉我

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

维基百科又和我说

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序（英语：Topological sorting）。

1. 每个顶点出现且只出现一次；
2. 若A在序列中排在B的前面，则在图中不存在从B到A的路径。

也可以定义为：拓扑排序是对有向无环图的顶点的一种排序，它使得如果存在一条从顶点A到顶点B的路径，那么在排序中B出现在A的后面^[1]。

想了解的自己去找，我就说这么多了。

下面步入正题。

看下面的样例。

不过要先说明一下输入格式：第一行一个整数N，之后的N行，每行若干个以0为结尾的整数。

表示第 i 个节点向这些个节点都有一条（有向）边。

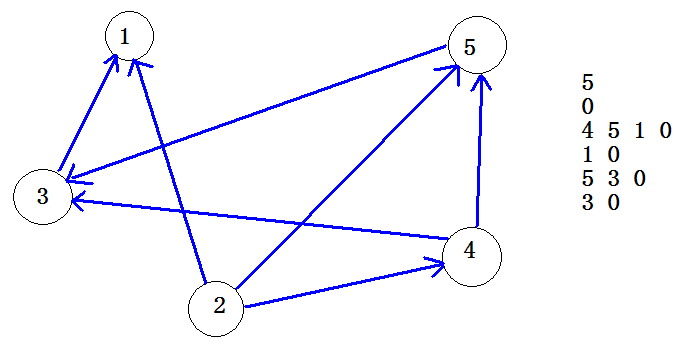
那么这张图的拓扑排序就是2 4 5 3 1当然可能并不唯一。

下图是他拓扑排序后变得更加直观的图

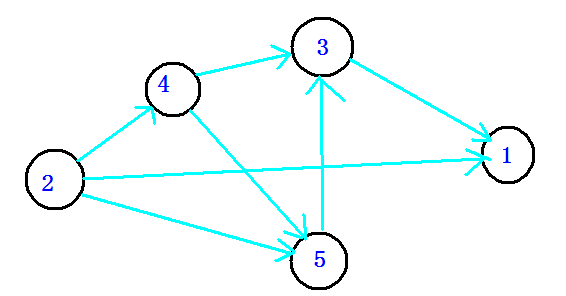
那么这个拓扑排序是如何实现的呢。

下面我们就来看看。

首先定义一个indgr数组，表示每个点的入度（就是有几条边是指向他的）。

定义一个栈。先将所有入度为0的点入栈。然后每次都把栈顶元素输出，并且弹出记录下来，还要用一个cnt记录输出次数。输出之后，把与相连的点的入度-1，如果-1之后这个点的入度变为了0，那么就将这个点入栈，重复此操作，直到所有的点都被输出一遍，也就是说cnt==n的时候就可以结束程序了。

下面是代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>

using namespace std;

stack<int> S;
int n, cnt;
int son, tot[105];
int indgr[108];
int ed[105][105];

int main() {
    scanf("%d", &n);
    for(int i=1; i<=n; i++) {
        while(scanf("%d", &son) == 1) {
            if(son == 0) {
                break;
            }
            ed[i][++tot[i]] = son;
            indgr[son]++;
        }
    }
    for(int i=1; i<=n; i++) {
        if(indgr[i] == 0) {
            S.push(i);
        }
    }
    while(cnt != n) {
        int k = S.top();
        printf("%d ", k);
        cnt++;
        S.pop();
        for(int i=1; i<=tot[k]; i++) {
            indgr[ed[k][i]]--;
            if(indgr[ed[k][i]] == 0) {
                S.push(ed[k][i]);
            }
        }
    }
    return 0;
}

作者：wlz

出处：http://www.cnblogs.com/bljfy/p/8729163.html

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。