dijkstra呢是最短路三大算法之一。很多人都觉得不如spfa,但是这两者在跑稠密图时,dijkstra有奇效
在讲之前先说一说食用方法:
适用于有向的无负权值的图。
样例飘过
6 9 1 //n个点,m条边,以s为起点 1 3 3 1 6 10 3 6 5 4 3 7 1 4 4 4 2 5 5 2 4 4 5 6 3 5 6
0 9 3 4 9 8
上面这组样例我们让他更直观一些
神图警报,请开启护眼模式
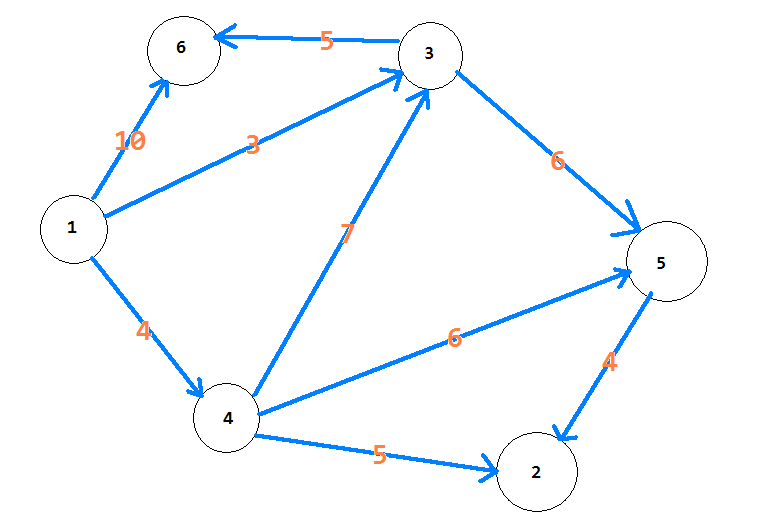
真心累
首先我们应该知道dijkstra的核心思想是贪心。
定义一个$dis$数组,$dis[i]$表示从起点到i节点的距离,我们在程序一开始的时候把dis全部赋值成INF,
只把dis[s]赋值成0,(因为s->s == 0),这时候我们需要定义一个bool行的数组book,book[i]表示节点是否被访问过。
那么接下来就进入核心部分了。
我们每次从所有的节点中找一个dis值最小的,当让我们知道第一次肯定会找到s,然后以这个点为节点向外扩展,如果在已知的边的基础上可以找到更短的到某一个点的路径,那么就将这个路径更新。
这么说可能有点抽象,那么让我们看点实在的
上图
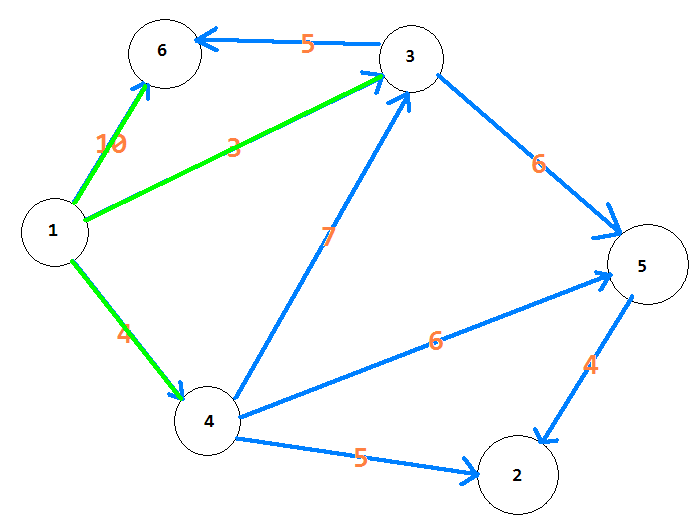
第一次找到了dis值最小的1号节点向外扩展,那么现在dis数组的值为
$dis[1] = 0, dis[2] = INF, dis[3] = 3, dis[4] = 4, dis[5] = INF, dis[6] = 10$
记得要把book[1]变成1,代表已经访问过。
接下来进行第二次扩展,这时候由于dis[1]我们已经访问过,所以接下来就会选择3号节点进行扩展
如图

从3号节点出去的边可以连到5和6,连5时毫无疑问会更新,但是再连6时,我们发现dis[6]已经扩展了一次,那么怎么办呢,很明显,从1走到3再走到6的话总路程为dis[3]加上3到6的路程,共为8,比现有的dis[6]要小,所以我们就要再更新dis[6] = 8;
通过这么一次次的更新,我们就能把这张图的最短路跑完,注意是单源最短路。
说了这么多我们来看下代码,但是我这个代码有个很玄学的地方,就是建边的时候我写的是用数组实现的邻接链表,但是原理是和结构体实现的邻接链表相同,大家将就着看,如果看不懂那就参考一下下面这篇文章
【坐在马桶上看算法】算法8:巧妙的邻接表(数组实现)
这里讲的非常的详细,我当初就是看的这里。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define MAXN 500008
#define INF 2147483647
#define maxn 10008
using namespace std;
int n, m, s;
int next[MAXN], first[MAXN];
int u[MAXN], v[MAXN], w[MAXN];
int dis[maxn];
bool book[MAXN];
int main() {
scanf("%d%d%d", &n, &m, &s);
for(int i=1; i<=n; i++) {
dis[i] = INF;
}
dis[s] = 0;
memset(first, -1, sizeof(first));
for(int i=1; i<=m; i++) {
scanf("%d%d%d", &u[i], &v[i], &w[i]);
next[i] = first[u[i]];
first[u[i]] = i;
}
for(int i=1; i<n; i++) {
int minn = INF, x;
for(int j=1; j<=n; j++) {
if(dis[j] < minn&&book[j] == 0) {
minn = dis[j];
x = j;
}
}
book[x] = 1;
int k = first[x];
while(k != -1) {
if(dis[v[k]] > dis[u[k]]+w[k]) {
dis[v[k]] = dis[u[k]]+w[k];
}
k = next[k];
}
}
for(int i=1; i<=n; i++) {
printf("%d ", dis[i]);
}
}