BZOJ3680: 吊打XXX（模拟退火）

Description

gty又虐了一场比赛，被虐的蒟蒻们决定吊打gty。gty见大势不好机智的分出了n个分身，但还是被人多势众的蒟蒻抓住了。蒟蒻们将
n个gty吊在n根绳子上，每根绳子穿过天台的一个洞。这n根绳子有一个公共的绳结x。吊好gty后蒟蒻们发现由于每个gty重力不同，绳
结x在移动。蒟蒻wangxz脑洞大开的决定计算出x最后停留处的坐标，由于他太弱了决定向你求助。
不计摩擦，不计能量损失，由于gty足够矮所以不会掉到地上。

Input

输入第一行为一个正整数n(1<=n<=10000)，表示gty的数目。
接下来n行,每行三个整数xi，yi，wi，表示第i个gty的横坐标，纵坐标和重力。
对于20%的数据，gty排列成一条直线。
对于50%的数据，1<=n<=1000。
对于100%的数据，1<=n<=10000,-100000<=xi,yi<=100000

Output

输出1行两个浮点数（保留到小数点后3位），表示最终x的横、纵坐标。

Sample Input

3
0 0 1
0 2 1
1 1 1

Sample Output

0.577 1.000

解题思路：

来，我们盗一张Google的图。

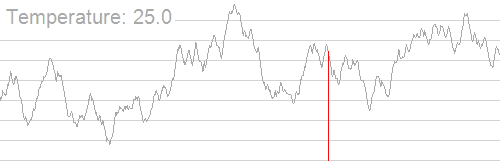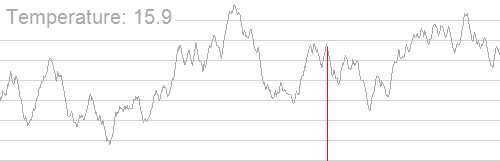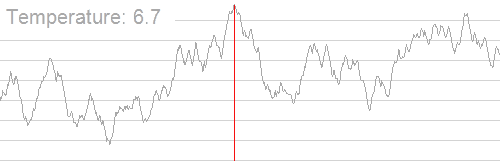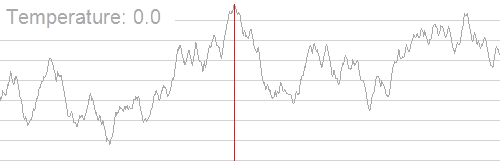
大概就是这样。

模拟退火，就是某位天才在AK了IPHO以后准备AKIOI时发明的，模仿物理中晶体缓慢降温时最后稳定的过程。

由于最后排列位置是不确定的，但能量比较低，分子热运动时会趋向于稳定时的位置，但也会有几率走到更不

稳定的位置。

大概就是这样的，只要让步幅与温度正相关就可以像温度降低时热运动变缓了。

这道题就让机械能最小就好了。

代码：

 1 #include<ctime>
 2 #include<cmath>
 3 #include<cstdio>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 const double delt=0.99;
 8 struct hole{
 9     double x,y,w;
10     void Ins(void)
11     {
12         scanf("%lf%lf%lf",&x,&y,&w);
13         return ;
14     }
15 }h[20000];
16 int n;
17 double ansx,ansy;
18 double ans=1e18;
19 double squ(double x)
20 {
21     return x*x;
22 }
23 double dist(int a,int b)
24 {
25     return sqrt(squ(h[a].x-h[b].x)+squ(h[a].y-h[b].y));
26 }
27 double Ep(double xx,double yy)
28 {
29     double ans=0.00;
30     h[n+1].x=xx;
31     h[n+1].y=yy;
32     for(int i=1;i<=n;i++)
33         ans+=dist(i,n+1)*h[i].w;
34     return ans;
35 }
36 void Simulate_Anneal(void)
37 {
38     double Tpt=4600;
39     while(Tpt>1e-15)
40     {
41         double tmpx=ansx+(rand()*2-RAND_MAX)*Tpt;
42         double tmpy=ansy+(rand()*2-RAND_MAX)*Tpt;
43         double tmpans=Ep(tmpx,tmpy);
44         if(tmpans-ans<0)
45         {
46             ansx=tmpx;
47             ansy=tmpy;
48             ans=tmpans;
49         }else if(exp((-tmpans+ans)/Tpt)*RAND_MAX>rand())
50         {
51             ansx=tmpx;
52             ansy=tmpy;
53             ans=tmpans;
54         }
55         Tpt*=delt;
56     }
57     return ;
58 }
59 int main()
60 {
61     srand(time(NULL));
62     scanf("%d",&n);
63     for(int i=1;i<=n;i++)
64         h[i].Ins();
65     Simulate_Anneal();
66     printf("%.3lf %.3lf
",ansx,ansy);
67     return 0;
68 }