LIBSVM (三) 葡萄酒种类识别

3.1 原始数据分析

1）测试数据为：wine data set，储存在chapter_WineClass.mat。classnumer = 3;wine,记录了178个样本的13个属性；wine_labels.178×1，记录了178个样本的各自类别标签。

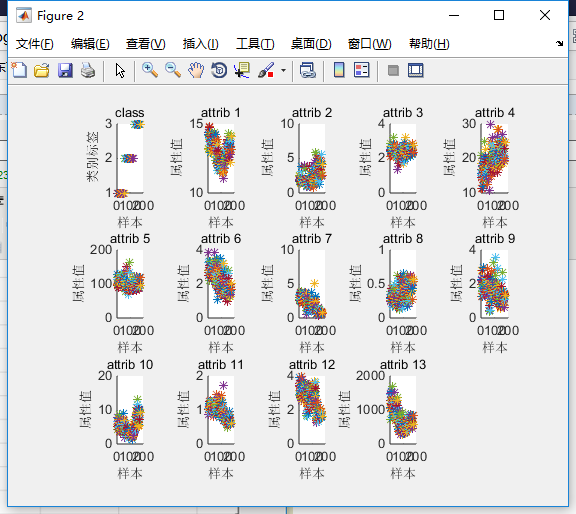
2）数据的可视化：13个指标的属性值即数据的箱式图；数据的分维可视化图。

% 画出测试数据的分维可视化图
figure
subplot(3,5,1);
hold on
for run = 1:178
    plot(run,wine_labels(run),'*');
end
xlabel('样本','FontSize',10);
ylabel('类别标签','FontSize',10);
title('class','FontSize',10);
for run = 2:14
    subplot(3,5,run);
    hold on;
    str = ['attrib ',num2str(run-1)];
    for i = 1:178
        plot(i,wine(i,run-1),'*');
    end
    xlabel('样本','FontSize',10);
    ylabel('属性值','FontSize',10);
    title(str,'FontSize',10);
end

 

3.2 模型建立及其实现

3.2.1 模型建立

　　首先从原始数据中把训练集和测试集提取出来，然后进行预处理，之后用训练集对SVM进行训练，最后用得到的模型来预测测试集的分类标签，算法流程如图：

选定训练集和测试集 → 数据预处理 → 训练SVM → 分类准确率 → 预测（测试集）

3.2.2 MATLAB 实现

1） 选定测试集和训练集

该数据一共有三类，现将每个类别分为两组，重新组合数据，一部分为训练集(train_wine)，一部分为测试集(test_wine)。

% 选定训练集和测试集
% 将第一类的1-30,第二类的60-95,第三类的131-153做为训练集
train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)];
% 相应的训练集的标签也要分离出来
train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)];
% 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集
test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)];
% 相应的测试集的标签也要分离出来
test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)];

 2） 数据预处理——归一化

　　 [0,1]区间归一化：y=(x-xmin)/(xmax-xmin);

　　 [-1,1]区间归一化：2*(x-xmin)/(xmax-xmin)-1;

　　mapminmax 函数实现：y=(ymax-ymin)×(x-xmin)/(xmax-xmin)+ymin,其中ymin和ymax是映射范围参数，可调节，默认值是-1和1。函数接口如下：

[y,ps] = mapminmax(x)
[y,ps] = mapminmax(x,ymin,ymax)
[x,ps] = mapminmax('reverse',y,ps)    %反归一化

 　　新的映射函数对x进行重新归一化方法：

[y,ps] = mapminmax(x);
ps.ymin = 0;
ps.ymax = 1;
[ynew,ps] = mapminmax(x,ps);

 　　wine 数据的归一化实现：

%% 数据预处理
% 数据预处理,将训练集和测试集归一化到[0,1]区间

[mtrain,ntrain] = size(train_wine);
[mtest,ntest] = size(test_wine);

dataset = [train_wine;test_wine];
% mapminmax为MATLAB自带的归一化函数
[dataset_scale,ps] = mapminmax(dataset',0,1);
dataset_scale = dataset_scale';

train_wine = dataset_scale(1:mtrain,:);
test_wine = dataset_scale( (mtrain+1):(mtrain+mtest),: );

 3） 分类及预测

%% SVM网络训练
model = svmtrain(train_wine_labels, train_wine, '-c 2 -g 1');

%% SVM网络预测
[predict_label, accuracy,dec_values] = svmpredict(test_wine_labels, test_wine, model);

%% 结果分析

% 测试集的实际分类和预测分类图
% 通过图可以看出只有一个测试样本是被错分的
figure;
hold on;
plot(test_wine_labels,'o');
plot(predict_label,'r*');
xlabel('测试集样本','FontSize',12);
ylabel('类别标签','FontSize',12);
legend('实际测试集分类','预测测试集分类');
title('测试集的实际分类和预测分类图','FontSize',12);
grid on;

 

3.3 案例扩展——归一化方式及核函数对准确了的影响

1）采用不同归一化方式的对比

a.不进行归一化处理

Accuracy = 39.3258% (35/89) (classification)

 b.[-1,1]归一化

[dataset_scale,ps] = mapminmax(dataset',-1,1);

Accuracy = 97.7528% (87/89) (classification)

c.[0,1]归一化

[dataset_scale,ps] = mapminmax(dataset',0,1);

Accuracy = 98.8764% (88/89) (classification)

 　　不同的归一化对最后的准确率会有一定的影响。并不是任何问题都必须事先把原始数据进行归一化，要具体问题具体看待，测试表明有时候归一化后的测试准确率比没有归一化的准确率会低很多。

2） 采用不同核函数的对比

a.linear

'-c 2 -g 1 -t 0'

Accuracy = 97.7528% (87/89) (classification)

b.polynomial

'-c 2 -g 1 -t 1'

Accuracy = 98.8764% (88/89) (classification)

c.radial basis function

'-c 2 -g 1 -t 2'

Accuracy = 98.8764% (88/89) (classification)

d.sigmoid

 '-c 2 -g 1 -t 3'

Accuracy = 52.809% (47/89) (classification)

 如何通过选取 c 和 g 的值提升分类器的性能？下个随笔将会具体介绍。