LeetCode 72. Edit Distance

72.Edit Distance（编辑距离）

题目：

　　给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

　　你可以对一个单词进行如下三种操作：

1. 1. 插入一个字符
   2. 删除一个字符
   3. 替换一个字符

思路：

　　多次选择试图得到最优解，那么考虑动态规划。

　　先假设word1有len1位，word2有len2位，建立数组step，step[i][j]就代表我们要将word1前 i 位转换为word2前 j 位的最少数量。

　　此时word1查找到第 i+1 位字母a，word2查找到第 j+1 位字母b，我们直接比较这两个字母，能得到两种情况：

　　1.a=b：那么就不需要操作，此时word1前 i+1 位替换为word2前 j+1 位只需要step[i][j]步

　　　　即为   step[ i+1 ][ j+1 ] = step[ i ][ j ] 

　　2.a!=b：就要在给定的三种操作方式中选择最优解，再增加一步操作即可

　　　　即为   step[ i+1 ][ j+1 ] = Min(num1，num2，num3);

　　最后得到的step[ i ][ j ]就是最短编辑距离。

图解：

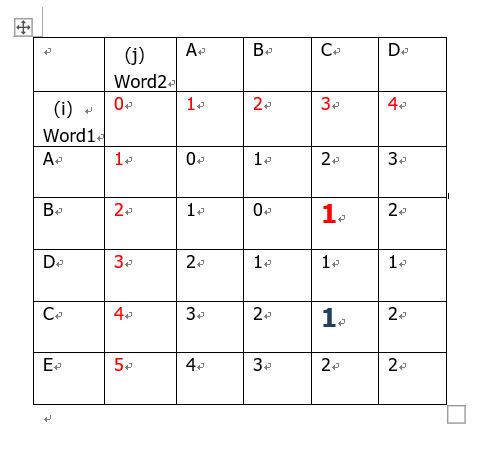
　　首先建立数组，将红色部分赋值，之后开始按照顺序计算，从word1转换为word2，step[ i ][ j ]就是最短编辑距离，step[ i-1][ j ]就是插入，step[ i ][ j-1 ]就是删除，step[ i-1 ][ j-1 ]就是修改，如果不相同就从三种决策中寻找最小值加一，相同就直接添加，值等于step[ i-1 ][ j-1 ]。

　　例如AB->ABC（大号红色字体），B和C不同，左侧（AB->AB）0次，左上（A->AB）1次，上方(A->ABC)2次，选择三种情况最小值，再进行一步操作（左侧AB->AB->ABC），只需要1次。

　　或者ABDC->ABC(大号蓝色字体)，C与C相同，直接进行左上（ABD->AB-ABC）,也只需要1次。

　　

代码：

　　

	public static int minDistance(String word1, String word2) 
	{
		int len1 = word1.length();
	    int len2 = word2.length();
	
	    int[][] step = new int[len1 + 1][len2 + 1];
	 
	    for (int i = 0; i <= len1; i++) 
	        step[i][0] = i;
	    for (int j = 0; j <= len2; j++) 
	        step[0][j] = j;
	    
	    for (int i = 1; i <= len1; i++) 
	    {
	        char letter1 = word1.charAt(i-1);
	        for (int j = 1; j <= len2; j++) 
	        {
	            char letter2 = word2.charAt(j-1);

	            if (letter1 == letter2) 
	            {   //若字母相同，即直接添加，不增加步数         
	                step[i][j] = step[i-1][j-1];
	            } 
	            else 
	            { 
	                int ReNum = step[i-1][j-1] + 1;
	                //修改
	                int InNum = step[i-1][j] + 1;
	                //插入
	                int DeNum = step[i][j-1] + 1;
	                //删除
	                int min = Math.min(ReNum,Math.min(InNum, DeNum));
	                step[i][j] = min;
	            }
	        }
	    }
	    return step[len1][len2];
    }