1.本周学习总结
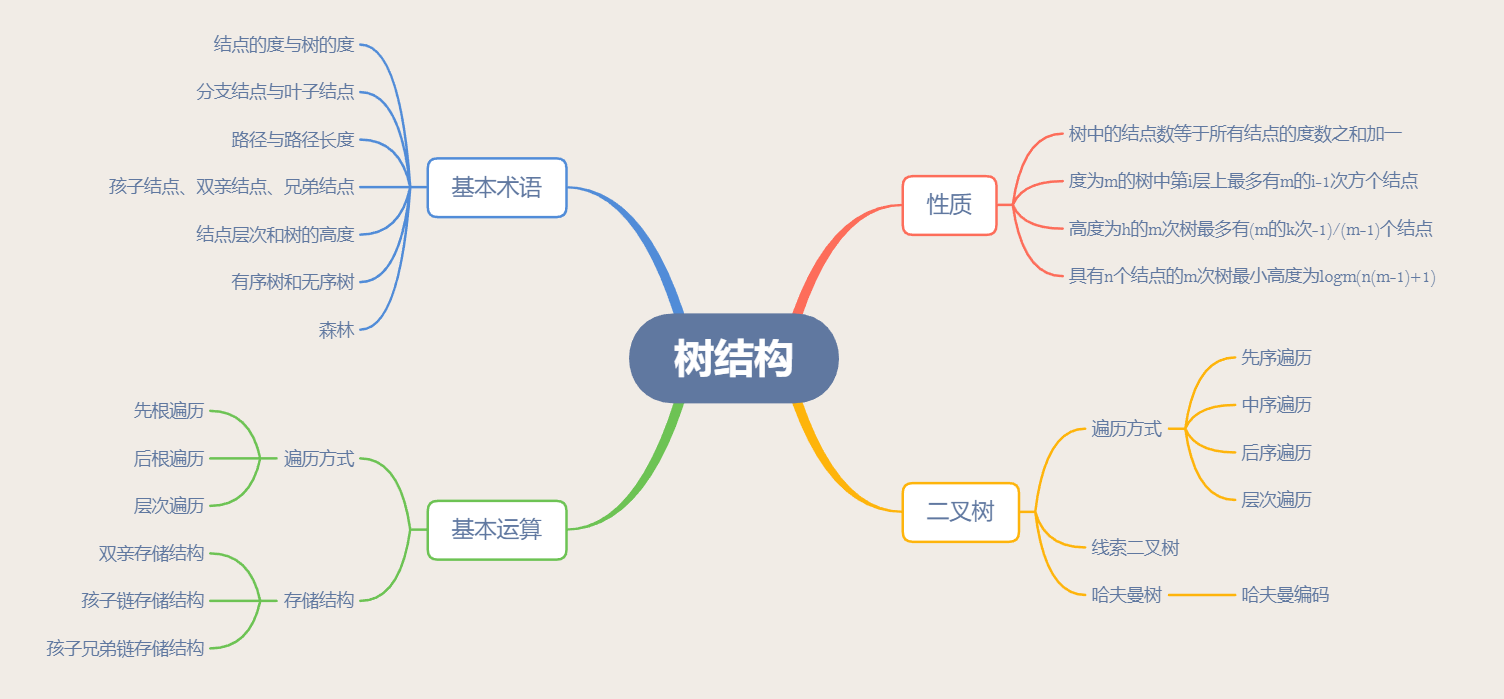
1.思维导图
2.谈谈你对树结构的认识及学习体会
- 本章主要学习了树结构的相关知识,树形结构属于非线性结构,常用的树形结构有树和二叉树。线性结构可以表示元素或元素之间的一对一关系,而在树行结构中,一个结点可以与多个结点相适应,因此能够表示层次结构的数据。树结构就是利用树的特点,以根节点作为树干,子树作为树枝,而最后的叶子结点作为树叶,组成大树,即树形结构体。树结构的特殊存储方式有二叉树,其衍生有线索二叉树和哈夫曼树,二叉树由一个根节点和两棵互不相交的左子树和右子树组成。二叉树的遍历方法有多种,其中后序遍历还可用来解决表达式求值问题。线索二叉树是利用空余的指针指向结点前驱,而哈夫曼树利用带权路径解决最优问题。
- 树结构的运用的核心部分就是递归,只有用好递归才能在运用树时更得心应手。其中递归体的设置和递归口尤为重要,递归体分为左子树和右子树,递归口分为结点为空和另设条件,传参时也可增加高度标记h和字符位置i。本次的大作业是利用树解决文档树和目录树,和同学合作完成使我了解到很多自身的不足,像主体的构建,函数的调用,命名的规范,错误的调试,都是我需要改进的。所以多向同学学习好的做法有利于自己对代码的处理,还需要通过自学一些新的头文件和函数容器,能让我们在解决问题的时候技高一筹,处理得更加轻松。
2.PTA实验作业
2.1.题目1:表达式树
输入一行中缀表达式,转换一颗二叉表达式树,并求解.
表达式只包含+,*,/,(,)运算符,操作数只有一位,且为整数(有兴趣同学可以考虑负数小数,两位数做法)。按照先括号,再乘除,后加减的规则构造二叉树。
2.1.1设计思路(伪代码)
void InitExpTree(BTree &T,string str)//建表达式的二叉树
建数字栈s,建符号栈op
定义计量数i为0
'#'入栈op
while str[i] do //遍历字符串
if !In(str[i]) then //数字作叶子结点
新建结构体指针T
T的data为str[i],初始化T的左右子树
T入栈s
i加一
else //字符为运算符时
switch Precede(op.top(),str[i]) then //符号优先级比较
若为'<',则str[i]入栈op且i加一
若为'=',op栈顶出栈且i加一
若为'>',新建结构体指针T
T的data为op栈顶且出栈
赋予T左右子树分别为s栈顶元素并让其出栈
T入栈s
end switch
end if
end while
while op栈顶不为'#' do //符号栈有余下运算符时的处理
新建结构体指针T
T的data为op栈顶,T的右子树为s栈顶并让其出栈
如果s不为空,则T的左子树为s栈顶并让其出栈
T入栈s
op栈顶出栈
end while
T为s栈顶
double EvaluateExTree(BTree T) //计算表达式树
定义数a和b
当左右子树为空时返回 T->data-'0'
a=EvaluateExTree(T->lchild) //递归
b=EvaluateExTree(T->rchild) //递归
以a,b为运算数,T->data为运算符进行四则运算,并处理除数为0的情况
2.1.2代码截图


2.1.3本题PTA提交列表说明

Q1:树在删除或添加子树时或通过栈操作字符串时容易出现空指针造成段错误
A1:在符号休先级的比较中,大于号和小于号的情况弄错造成出栈和入栈时操作错误;同时在递归运用上,树的分支传参和递归口没有设置好,也导致了段错误。
Q2:在树的数据进行出栈入栈操作后,可能会出现符号栈中有剩余运算符没有进行运算
A2:这就需要另设循环将运算符中的数据通过符号栈中的符号进行运算,当符号栈顶为‘#’时结束循环即所有运算符已经运算。
2.2.题目2:二叉树叶子结点带权路径长度和
二叉树叶子结点的带权路径长度指:叶子结点的权重路径长度。本题要求算出二叉树所有叶子结点的带权路径长度和。
2.2.1设计思路(伪代码)
struct BTNode //定义树的结构体
数据data
左子树指针Left
右子树指针Right
int main()
定义计量数i=1
定义高度初始量h=0
字符串定义str并输入字符串
定义建树指针并赋予建树函数返回值
定义权重路径长度wpl并赋予求权函数返回值
输出wpl
BinTree CreateBtree(string str,int i) //递归建树
当i超过字符个数或者字符为'#'时,返回NULL //递归口
新建树结构指针BT
BT的data为当前字符 //写入字符串中的数据
左子树指针为CreateBtree(str,2*i)
右子树指针为CreateBtree(str,2*i+1)
返回根节点指针BT
int GetWpl(BinTree BT,int h) //递归求权重路径长度
定义权重wpl
当BT为空时return 0 //BT为空时结束递归
当左右子树都为空时,权重为结点数据乘高度,返回权重 //BT为叶子结点时结束递归
高度加一
返回GetWpl(BT->Left,h)加GetWpl(BT->Right,h) //返回值累加
2.2.2代码截图

2.2.3本题PTA提交列表说明

Q1:在devC上运行成功并验证答案后才在pta提交,所以题目列表较少
A1:其中遇到的问题和解决有,建树函数中i的传参公式,递归口的附加条件即字符串长度判断,求权时高度的代入运用参数h,字符数据需要转化为数字。
Q2:pta上有的样例正确对,但有的样例错误
A2:后发现在递归口的附加条件即字符串长度判断上,用i>str.length()不能准确结束递归,需要改成i>str.size()-1才能正确。
2.3.题目3:输出二叉树每层节点
层次遍历树中所有节点。输出每层树节点。
树结构按照树的先序遍历递归建树,比如先序遍历字符串“ABD#G###CEH###F###”#代表空节点。
2.3.1设计思路(伪代码)
struct BTNode //定义树的结构体
定义数据data
定义左子树指针Left,右子树指针Right
int main()
定义计量数i,初始高度h,层数比较t
定义高度H
定义字符串变量str并输入字符串
定义树根节点指针BT并调用建树函数
通过求高函数求得高度H
当高度为0时输出"NULL"并结束程序 //树为空
循环调用输出函数,按层输出
BinTree CreateBtree(string str,int &i) //递归建树
当i超过字符个数或者字符为'#'时,返回NULL //递归口
新建树结构指针BT
BT的data为当前字符 //写入字符串中的数据
左子树指针为CreateBtree(str,++i)
右子树指针为CreateBtree(str,++i)
返回根节点指针BT
int GetHeight(BinTree BT) //求高度
定义左右子树高度为H1,H2
当BT为NULL时返回0 //BT为空时结束递归
H1=GetHeight(BT->Left) //递归
H2=GetHeight(BT->Right)
返回H1和H2中较大的值加一
void PrintfBT(BinTree BT,int h,int t) //输出该层的字符
当BT为NULL时返回 //BT为空时结束递归
h加一
当h==t时输出结点字符和','
PrintfBT(BT->Left,h,t); //递归
PrintfBT(BT->Right,h,t);
2.3.2代码截图


2.3.3本题PTA提交列表说明

Q1:定义变量名和函数名时,首字母或中间字母的大小写出现不统一,导致编译错误
A1:命名函数时采用驼峰命名法,指针全部大写,规范命名,减小后期处理的工作量。
Q2:题目要求树结构按照树的先序遍历递归建树,这导致字符串的字符读取不容易运用
A2:采用&定义参数i,用i表示当前字符串中需要用到的数据位置,即每次先序新建结点时,都能让i同步加一,这样就能防止一个数据重复赋值。
Q3:由于需要逐层输出数据,但不能顺序遍历树结构
A3:编写一个求高函数求出树的高度,既可以处理树为空的情况也用来作为后来输出的终止条件。输出函数中的参数h为当前层数,t为需要输出的层数,这样每次遍历树就能输出第t层的数据,遍历h次即完成按层输出。
3.阅读代码
3.1 题目

3.2 解题思路
- 用结构体file来作为树的节点,其中包含char name[261]存储文件名,bool型变量isDirectory表示是目录还是文件,bool型变量visited用来表示dfs过程中该文件节点是否被访问过,vector
型变量subFiles存储其子目录。由于题目给的每个字符串,表示的都是从root的第一个孩子开始的路径,因此用一个vector 型变量files存储每个字符串中的文件值,依次将files中的文件通过函数void add(file &f, int index)添加进以root为根的树中。 - void add(file &f, int index)函数实现:由于会改变f文件的subFile值,所以需要传递引用。如果index == files.size(),说明已经遍历完了files中的所有文件,直接return。遍历f的子目录,寻找与files[index]名字相同且同是文件或同是目录的文件,如果找到,说明files[index]已经在f的子目录中,考虑第index + 1个文件,即递归地调用该函数add(f.subFiles[i], index + 1),并且返回。如果没有在f的子目录中寻找到files[index],将files[index]加入f的子孩子中,并且递归地调用该函数add(f.subFiles[f.subFiles.size() - 1], index + 1)。
- void dfs(file &nowVisit, int level)函数实现:由于会对f文件的subFile进行排序,所以需要传递引用。如果当前文件还未被访问过,标记其已被访问,并且对其subFile进行排序。输出当前空格数和文件名。对其subFile里的文件,递归调用dfs函数,注意level需加2。
3.3 代码截图


3.4 学习体会
- 通过大作业文档树的编写加上目录树的学习,我更加熟悉了树结构。目录树的构建,主要思路是先建树,再深度优先遍历。树以层层递进的构建形式为特殊点,应用于资料和文件归纳,也作为目录。也正是由于这个特点,递归的逐层深入的特点也使其在树操作中被广泛应用。
- 在这道题目中,还有个新的知识点就是使用了vector容器。vector类称作向量类,它实现了动态数组,用于元素数量变化的对象数组。像数组一样,vector类也用从0开始的下标表示元素的位置;但和数组不同的是,当vector对象创建后,数组的元素个数会随着vector对象元素个数的增大和缩小而自动变化。vector也有一些结构自带的函数,所以在解题时直接套用也是很方便的。所以还是一句古话“技多不压身”,多学一些新函数,能让自己解题得更轻松。