1.本周学习总结
1.1.思维导图
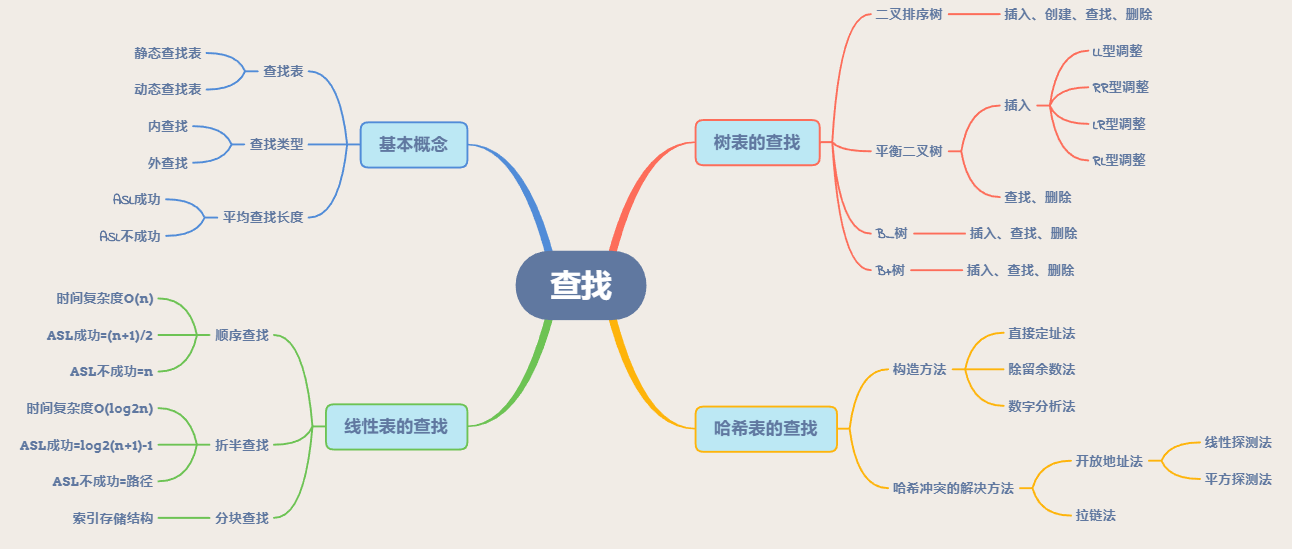
1.2.对查找运算的认识及学习体会
- 本章学习了查找的相关知识,介绍了线性表查找、数表查找和哈希表查找等相关算法设计查找算法。查找又称为检索,是指在某种数据结构种找出满足给定条件的元素。查找是一种十分有用的操作,例如在学生成绩表种查找某个学生的成绩元素,在图书馆的书目文件中查找某编号的图书元素等。因为查找是对已存入到计算机中的数据进行的运算,所以在研究各种查找方法时,首先必须弄清这些查找方法所需要的数据结构是什么,对表中关键字的次序有何要求,例如是对无序数据还是对有序数据查找。查找是一种实用工具,所以就有了平均查找长度ASL这个指标来衡量它的性能。一个查找算法的ASL越大,其时间性能越差,反之则ASL越小,其时间性能越好。
- 通过学习查找的相关算法和函数,能方便我们在之后的编程中快速找到合适的遍历方法,提高程序的时间性能;在基于大数据上,平衡二叉树里的特殊树的建立通过对大数据的整理处理,方便了对大数据的操作;在存储数据时,使用哈希表的存储结构能使查找的目标更加明确,提高查找效率。所以作为数据结构的查找算法,也是一种提高程序效率的实用算法。
2.PTA实验作业
2.1.题目1:是否二叉搜索树
本题要求实现函数,判断给定二叉树是否二叉搜索树,如果T是二叉搜索树,则函数返回true,否则返回false
2.1.1设计思路(伪代码)
bool IsBST ( BinTree T ) //判断给定的T是否二叉搜索树
if 树为空或没有孩子结点时返回true
else if 递归访问左、右孩子结点,若其中一个返回false,则返回false
else if
!(左子树?结点>左结点:1且右子树?结点<右结点:1) 则返回false
else
定义子树指针TLeft,TRight
如果T->Left不为空,TLeft指向左子树最大值
如果T->Right不为空,TRight指向右子树最小值
返回左子树?(结点>TLeft->Data):1且右子树?(结点<TRight->Data):1
end if
2.1.2代码截图

2.1.3本题PTA提交列表说明

Q1:利用二叉搜索树的特性来设计函数
A1:非空左子树的所有键值小于其根结点的键值,非空右子树的所有键值大于其根结点的键值,当所有子树都满足这个条件时返回true。
Q2:部分正确的原因是没有考虑到空树的情况
A2:则加上if-else条件判断,若T为空也符合二叉搜索树的特性,则直接返回true。
ps:这道题省去第二、三行即不用递归的话,也是能神奇地做对的。
2.2.题目2:哈希表操作集
输入一组数据,建立哈希表,哈希函数为 h(k)=k%p,哈希冲突解决办法为线性探查法
2.2.1设计思路(伪代码)
void InsertHT(HashTable ha,int &n,KeyType k,int p)
//哈希表插入数据,n表示哈希表数据个数,k插入关键字,p除数
定义并计算哈希函数值adr=k%p
if ha[adr]的关键字为NULLKEY或DELKEY then
ha[adr].key置为k
ha[adr].count置为1
else //线性探测法
i为1
循环线性探测,找到key为空的地址adr
ha[adr].key置为k
ha[adr].count置为i
end if
void CreateHT(HashTable ha,KeyType x[],int n,int m,int p)
//创建哈希表,x为输入数组,n输入数据个数,m为哈希表长度,这里假设m=p
初始化哈希表的关键字和探测值
for n次 do //插入关键字
调用函数InsertHT()
end for
int SearchHT(HashTable ha,int p,KeyType k)
//在哈希表中查找关键字k,找不到返回-1,找到返回查找地址
定义并计算哈希函数值adr=k%p
初始化探测次数i为1
while ha[adr].key不为空 do
i++
adr=(adr+1)%p //线性探测
end while
if ha[adr].key等于k则返回adr //查找成功
else uns_count=i并返回-1 //查找失败
2.2.2代码截图

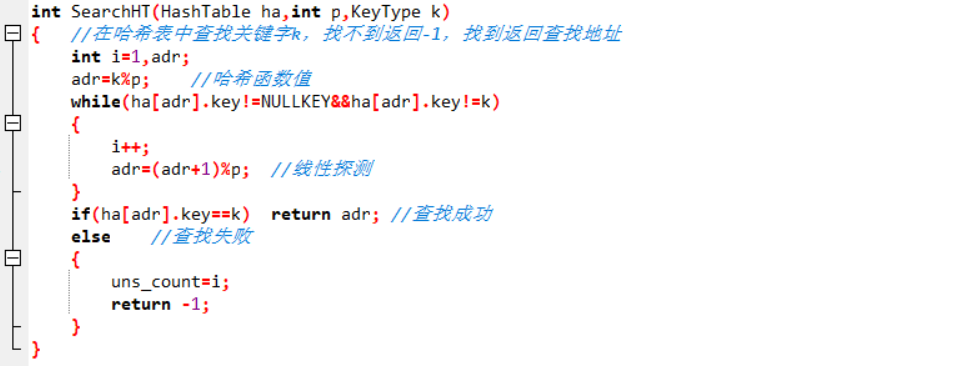
2.2.3本题PTA提交列表说明

Q1:题目考查的是哈希表的线性探查法的基本操作,采用开放地址法建立哈希表
A1:函数的大体是参考课本上的,其中省略了n的引用型传参,修改了函数参数和最后的返回算法。
Q2:答案错误后反复观察代码没有发现错误,觉得主要的问题是卡在一个小错误点上
A2:三个函数中的形参名字基本一样,采用查看调试不能方便看清,所以后来改用printf调试发现查找的函数中返回的值应该是adr而不是i。
2.3.题目3:QQ帐户的申请与登陆
实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是:据说现在的QQ号码已经有10位数了
2.3.1设计思路(伪代码)
定义三个字符串为三个信息order,id,password
定义N为指令行数并输入
for(N次)
输入数据order,id,password
if order等于"N" then //新建号码
当找不到id时
mp[id]置为password
输出"New: OK"
否则 输出"ERROR: Exist"
else //登陆号码
找不到id时,输出"ERROR: Not Exist"
账号密码不匹配时,输出"ERROR: Wrong PW"
否则,输出"Login: OK" //登陆成功
end if
end for
2.3.2代码截图

2.3.3本题PTA提交列表说明

Q1:账号密码逐一对应,且具有唯一性,但账号过长不能使用数组存储
A1:map容器提供一对一的数据处理能力,由于这个特性在处理账号密码的时候,在配对上提供快速通道。
Q2:在找不到id时的判断条件设置错误,导致题目答案错误
A2:用find函数来定位数据出现位置,它返回的一个迭代器,当数据出现时,它返回数据所在位置的迭代器,如果map中没有要查找的数据,它返回的迭代器等于end函数返回的迭代器,故当mp.find(id)==mp.end()时即找不到id。
3、阅读代码
3.1 题目:这是二叉搜索树吗?

3.2 解题思路
题目要求判断这是否是对一棵二叉搜索树或其镜像进行前序遍历的结果,如果数组可以构成前序遍历的二叉搜索树,那么对于根节点来说,左子树中最大的应该是左子树中最后一个叶节点,右子树最小的是右子树第一个叶节点,两者的下标之差为1. 题目说可能会是镜像的二叉搜索树,如果不满足二叉搜索树,再判断是否为镜像的二叉搜索树,都不是输出NO。如果是,把前序遍历的二叉搜索树用后序遍历输出。
3.3 代码截图


3.4 学习体会
这份代码是用数组建树,利用vector容器来处理结点,由于是对树的处理,所以递归构造函数是必不可少的。在网上找代码的时候,我发现容器的使用和声明定义非常普遍,这样做可以使代码的编程量减少,解题更容易。这道题的特殊点在于#define read(x) scanf("%d",&x),把输出代码声明成一个简单的函数,这种做法可以使代码看起来更简洁更高端,这是我以前没有见过的骚操作,学习到了。