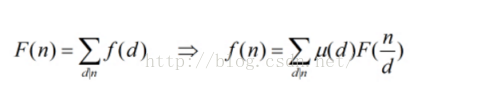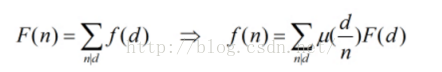这里学习一下莫比乌斯反演
翻看了很多书,发现莫比乌斯反演,准确来说不是一种固有的公式,而是一种法则。
我们定义F(n),为f(d)的和函数,而定义f(n)为某儿算术函数。
反演公式1:反演n的因子时
废话不用多说,直接引入题目:
HDU-1695-GCD
给出a,b,c,d,k,
问[a,b]和[c,d]区间内部有多少不同的gcd(x,y)=k的对数目。
那么我们可以把GCD(x,y)进行分解。
由于某两个数的GCD是k,那么把这两个数除以K,那么这两个数的值,一定互质。那么我们可以这样。把区间变为[a/k,b/k],找到这个区间内部,GCD(X,Y)==1的对数。
怎么用好反演函数呢??
首先我们要把F(n)和f(d)的意义赋予好的定义。
这道题要求的是对数,那么求和函数F(d)为 有多少对(x,y)满足 gcd(x,y)== d 的倍数 。f(d)为有多少对(x,y)满足 gcd(x,y)== d 。
很明显,我们需要用
这样理解,F(n)代表gcd(x,y)==n的倍数的个数,它的值其实等于所有n的倍数d的gcd(x,y)==d组数的和。
这样我们就成功反演了。并且我们需要的是gcd(x,y)=1那么带入n=1,那么这个值就非常容易算了,我们
就只需要算当d=i时,他的F(i)是多少,这就是代码,这个区间内部,gcd(x,y)==k*i(意思是gcd(x,y)为i及其倍数的)个数,这个其实就非常简单了,n/i * m/i即可,意思是x在一个范围内所有i的倍数,乘以y能取到的所有i的倍数的个数相乘,就是答案,最后做和。不过题目忽略了(x,y)和(y,x)那么我们需要在相同区间的就是能取到(x,y)(y,x)的部分,重新计算这个值,然后除以2即可。
#include<iostream> #include<stdio.h> #include<string.h> #include<algorithm> #define LL long long using namespace std; const int maxn = 1000000+50; const int INF = 0x3f3f3f3f; int miu[maxn]; bool vis[maxn]; int prime[maxn]; int mu[maxn]; int a,b,c,d,k; void init(){ int M=maxn; memset(prime,0,sizeof(prime)); memset(mu,0,sizeof(mu)); memset(vis,0,sizeof(vis)); mu[1]=1; int cnt=1; for (int i=2;i<maxn;i++){ if (!vis[i]){//质数 prime[cnt++]=i; mu[i]=-1;//质数的mobius为-1 } for (int j=1;j<cnt && i*prime[j]<maxn ;j++){ vis[i*prime[j]]=1;//筛掉 if (i%prime[j])mu[i*prime[j]]=-mu[i]; else { mu[i*prime[j]]=0; break; } } } } int main(){ int t; scanf("%d",&t); int ca=0; init(); while(t--){ ca++; scanf("%d%d%d%d%d",&a,&b,&c,&d,&k); if (k==0){ printf("Case %d: 0 ",ca); continue; } if (b>d)swap(b,d); b=b/k; d=d/k; LL ans1=0,ans2=0; for (int i=1;i<=b;i++){ ans1+=(LL)mu[i]*(b/i)*(d/i); } for (int i=1;i<=b;i++){ ans2+=(LL)mu[i]*(b/i)*(b/i); } printf("Case %d: %lld ",ca,ans1-ans2/2); } return 0; }